Serangkaian contoh dan latihan kekuatan

A Seri Kekuatan Itu terdiri dari sejumlah istilah dalam bentuk kekuatan variabel X, atau lebih umum, dari X-C, Di mana C Itu adalah bilangan real yang konstan. Dalam penjumlahan jumlah serangkaian kekuatan itu dinyatakan sebagai berikut:

∑A_N (X -c)^N = a_{salah satu} + ke₁ (x - c) + a₂ (X - c)² + ke₃ (X - c)³ +... + a_N (X - c)^N

Dimana koefisiennya_{salah satu}, ke₁, ke₂... mereka adalah bilangan real dan seri dimulai pada n = 0.

Gambar 1. Definisi Seri Daya. Sumber: f. Zapata.

Seri ini difokuskan pada nilai C itu konstan, tetapi Anda dapat memilih itu C Menjadi sama dengan 0, dalam hal ini kekuatan disederhanakan:

∑A_N X^N = a_{salah satu} + ke₁ x + a₂ X² + ke₃ X³ +... + a_N X^N

Serial ini dimulai dengan ke_{salah satu}(X-C)⁰ Dan ke_{salah satu}X⁰ masing -masing. Tapi kita tahu itu:

(X-C)⁰= x⁰ = 1

Karena itu ke_{salah satu}(X-C)⁰ = ke_{salah satu}X⁰ = ke_{salah satu} (Istilah mandiri)

Hal yang baik tentang kekuatan kekuatan adalah bahwa dengan mereka dapat mengekspresikan fungsi dan ini memiliki banyak keuntungan, terutama jika Anda ingin bekerja dengan fungsi yang rumit.

Ketika hal ini terjadi, alih -alih secara langsung menggunakan fungsi, pengembangan daya digunakan, yang dapat lebih mudah didapat, diintegrasikan, atau bekerja secara numerik.

Tentu saja semuanya dikondisikan untuk konvergensi seri ini. Seri konvergen saat dengan menambahkan sejumlah persyaratan, nilai tetap diperoleh. Dan jika kami menambahkan lebih banyak istilah, kami terus mendapatkan nilai itu.

[TOC]

Berfungsi sebagai kekuatan kekuatan

Sebagai contoh fungsi yang dinyatakan sebagai serangkaian kekuatan, mari kita ambil f (x) = e^X.

Fungsi ini dapat diekspresikan dalam hal serangkaian kekuatan sebagai berikut:

Dan^X  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Di mana! = n. (N-1). (N-2). (N-3)… dan diambil 0! = 1.

Kami akan memeriksa dengan bantuan kalkulator, yang seri ini secara efektif bertepatan dengan fungsi yang diberikan secara eksplisit. Misalnya, mari kita mulai melakukan x = 0.

Dapat melayani Anda: probabilitas teoretis: cara mengeluarkannya, contoh, latihan

Kami tahu itu e⁰ = 1. Mari kita lihat apa yang dilakukan serial ini:

Dan⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +... = 1

Dan sekarang mari kita coba x = 1. Kalkulator melempar itu Dan¹ = 2.71828, Dan kemudian mari kita bandingkan dengan seri:

Dan¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) + ... = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +… ≈ 2.7167

Dengan hanya 5 istilah kita sudah memiliki kebetulan yang tepat E ≈ 2.71. Seri kami hilang sedikit lebih banyak, tetapi karena lebih banyak istilah ditambahkan, dengan semua pasti seri konvergen dengan nilai yang tepat Dan. Representasinya tepat saat N → ∞.

Jika analisis sebelumnya diulangi n = 2 Hasil yang sangat mirip diperoleh.

Dengan cara ini kami yakin bahwa fungsi eksponensial f (x) = e^X Ini dapat diwakili oleh serangkaian kekuatan ini:

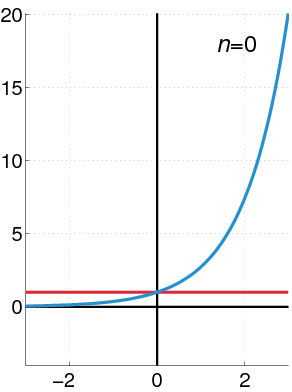Gambar 2. Dalam animasi ini dipandang sebagai kekuatan lebih dekat dengan fungsi eksponensial karena lebih banyak istilah yang diambil. Sumber: Wikimedia Commons.

Kekuatan geometris kekuatan

Fungsinya f (x) = e^X Ini bukan satu -satunya fungsi yang mengakui representasi serial kekuatan. Misalnya, fungsinya  F(x) = 1/1 - x  Itu sangat mirip dengan yang diketahui Seri geometris konvergen:

∑A.R^N = A / 1 - r

Lakukan saja a = 1 dan r = x untuk mendapatkan seri yang sesuai dengan fungsi ini, yang berpusat pada C = 0:

Namun, diketahui bahwa seri ini konvergen untuk │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Ketika Anda ingin mendefinisikan fungsi ini dalam interval lain, itu hanya berfokus pada nilai yang memadai dan siap.

Bagaimana menemukan seri pengembangan kekuatan fungsi

Fungsi apa pun dapat dikembangkan dalam serangkaian kekuatan yang difokuskan pada C, selama Anda berasal dari semua pesanan di x = c. Prosedur ini memanfaatkan teorema berikut, disebut Teorema Taylor:

Biarkan f (x) menjadi fungsi dengan turunan pesanan N, dilambangkan sebagai F^(N), yang mengakui pengembangan serial kekuatan dalam interval yo. Perkembangannya di Seri Taylor adalah:

Itu dapat melayani Anda: apa lokasi dari seluruh angka dan desimal?

Sehingga:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +… r_N

Dimana r_N, yang merupakan ke -n dari seri ini, disebut residu:

Saat C = 0 Serial ini dipanggil Seri Maclaurin.

Serial yang diberikan di sini identik dengan seri yang diberikan di awal, hanya sekarang ada cara untuk secara eksplisit menemukan koefisien dari setiap istilah, yang diberikan oleh:

Namun, harus dipastikan bahwa seri tersebut menyampaikan fungsi yang ingin Anda wakili. Kebetulan tidak setiap seri Taylor harus konvergen ke f (x) yang ada dalam pikiran saat menghitung koefisien ke_N.

Ini terjadi karena mungkin yang berasal dari fungsi, dievaluasi x = c bertepatan dengan nilai yang sama dari mereka yang berasal dari yang lain, juga di x = c. Dalam hal ini, koefisien akan sama, tetapi pengembangannya akan ambigu dengan tidak memiliki kepastian fungsi mana yang sesuai.

Untungnya ada cara untuk mengetahui:

Kriteria konvergensi

Untuk menghindari ambiguitas, jika r_N → 0 Saat n → ∞ untuk semua x dalam interval i, seri konvergen ke f (x).

Latihan

- Latihan diselesaikan 1

Temukan kekuatan geometris untuk fungsi f (x) = 1/2 - x fokus pada c = 0.

Larutan

Fungsi yang diberikan harus diekspresikan dengan cara yang cocok dengan sebanyak mungkin dengan 1 / 1- X, yang serialnya diketahui. Oleh karena itu kami menulis ulang pembilang dan penyebut, tanpa mengubah ekspresi asli:

1/2 - x = (1/2) / [1 - (x / 2)]]

Karena ½ konstan, ia keluar dari jumlah, dan ini ditulis dalam hal variabel baru x/2:

Dapat melayani Anda: binomial terkonjugasi: bagaimana itu diselesaikan, contoh, latihan

Perhatikan bahwa x = 2 bukan milik domain fungsi, dan sesuai dengan kriteria konvergensi yang diberikan di bagian tersebut Seri geometris daya, Pengembangan berlaku untuk │x/2│< 1 o equivalentemente -2 < x < 2.

- Latihan diselesaikan 2

Temukan 5 istilah pertama dari pengembangan seri Maclaurin dari fungsi f (x) = sen x.

Larutan

Langkah 1

Pertama adalah turunannya:

-Berasal dari Urutan 0: Ini adalah fungsi yang sama f (x) = sen x

-Turunan pertama: (sin x) '= cos x

-Turunan kedua: (sin x) "= (cos x) '= - sin x

-Turunan ketiga: (sin x) "= (-sen x) '= - cos x

-Turunan keempat: (sin x) "= (- cos x) '= sin x

Langkah 2

Maka setiap turunan dievaluasi pada x = c, seperti perkembangan maclaurin, c = 0:

sin 0 = 0; cos 0 = 1; - sen 0 = 0; -Cos 0 = -1; sin 0 = 0

Langkah 3

Koefisien dibangun untuk_N;

ke_{salah satu} = 0/0! = 0; ke₁ = 1/1! = 1; ke₂ = 0/2! = 0; ke₃ = -1 / 3!; ke₄ = 0/4! = 0

Langkah 4

Akhirnya seri ini dirakit menurut:

sin x ≈ 0.X⁰ + 1. X¹ + 0 .X² - (1/3!) X³ + 0.X⁴... = x - (1/3!)) X³  +..

Apakah pembaca membutuhkan lebih banyak istilah? Berapa banyak lagi, seri ini lebih dekat dengan fungsi.

Perhatikan bahwa ada pola dalam koefisien, istilah non -non -non -baru berikut ini₅ Dan semua indeks aneh juga berbeda dari 0, bergantian tanda -tanda, sehingga:

Sen x ≈ x - (1/3!)) X³  + (1/5!)) X⁵ - (1/7!)) X⁷  +.. .

Itu dibiarkan sebagai latihan untuk memverifikasi, Anda dapat menggunakan rasio hasil bagi Untuk konvergensi seri.

Referensi

1. Yayasan CK-12. Seri Daya: Representasi Fungsi dan Operasi. Dipulihkan dari: CK12.org.
2. Engler, a. 2019. Kalkulus integral. Universitas Nasional Pantai.
3. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
4. Teks Matematika Gratis. Seri Kekuatan. Pulih dari: matematika.Liibretexts.org.
5. Wikipedia. Seri Kekuatan. Pulih dari: is.Wikipedia.org.