Aplikasi Seri Fourier, contoh dan latihan diselesaikan

Itu Seri Fourier Mereka terdiri dari sejumlah istilah yang tak terbatas, yang terdiri dari fungsi harmonik, sinus dan kosinus, yang argumennya merupakan fundamental dari frekuensi mendasar.

Fungsi sinus dan kosinus dikalikan dengan koefisien nilai, sehingga jumlahnya identik dengan fungsi dengan periode t sama dengan dua kali pi (2π) dibagi dengan frekuensi sudut fundamental Ω Ω.

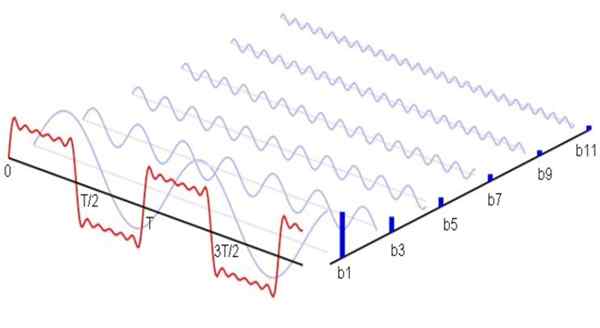
Gambar 1. Berikut adalah (berwarna biru) harmonik non -non -non -non -non -non -non -non -non -non -non -non -non -non -non -non -non -non -non -non -non -non. Jumlah harmonik ini memunculkan sinyal merah. Sumber: Wikimedia Commons.

Secara matematis itu akan dinyatakan sebagai berikut: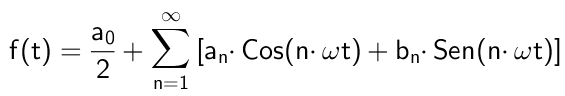

Di mana Ω Ini adalah frekuensi mendasar, yang terkait dengan periode tersebut T dari fungsi tersebut f (t) Melalui hubungan: 

Ω = 2π / t

Untuk menjadi periode berkala T, fungsinya f (t) memenuhi kondisi ini:

f (t) = f (t + k t)

Di mana k Itu adalah bilangan bulat dan koefisien untuk₀ , ke_N dan B_N Mereka disebut Koefisien Fourier.

[TOC]

Pentingnya dan Penggunaan Seri Fourier

Nama Fourier Series adalah karena fakta bahwa penemu adalah matematika Prancis.

Penemuan ini sangat mendasar untuk matematika, karena jika persamaan diferensial memiliki solusi harmonik tertentu, maka dimungkinkan untuk mencapai solusi umum dengan cara tumpang tindih atau jumlah yang sama.

Koefisien Fourier dari fungsi periodik, juga disebut tanda, Mereka adalah spektrum yang sama.

Oleh karena itu, spektrum adalah himpunan frekuensi yang membentuk sinyal yang ditandai oleh amplitudo setiap frekuensi, yang sesuai dengan nilai koefisien Fourier.

Sistem kompresi sinyal atau bentuk gelombang audio dan video, di bagian belakang jumlah bit yang secara signifikan lebih kecil daripada sinyal digital asli.

Seri Sinyal Fourier seperti sidik jarinya, dalam arti bahwa, diketahui koefisien yang mengada -ada, Anda selalu dapat mengetahui tanda mana yang menjadi milik mereka.

Meskipun penggunaan seri Fourier, atau bentuknya yang paling umum, Transformasi Fourier, Sebagai metode kompresi sinyal telah dikenal selama beberapa waktu, penggunaannya dalam praktiknya harus menunggu prosesor numerik cukup cepat, yang memungkinkan sinyal untuk dikompresi dan didekompresi dalam "waktu nyata".

Dapat melayani Anda: variabel statistik

Contoh Seri Fourier 

Selanjutnya, contoh fungsi f (t) dan seri Fourier -nya.

Fungsinya adalah:

 f (t) = 0 ya 0 ≤ t  < π y 1 si π ≤  t   < 2π

Dan memiliki seri Fourier yang sesuai diberikan oleh:

f (t) = ½ - 2/π⋅se (t) - 2/(3π) ⋅se (3t) - 2/(5π) ⋅sen (5t) - 2/(7π) ⋅sen (7t) -…

Gambar berikut menunjukkan fungsi dan jumlah parsial dari seri Fourier:

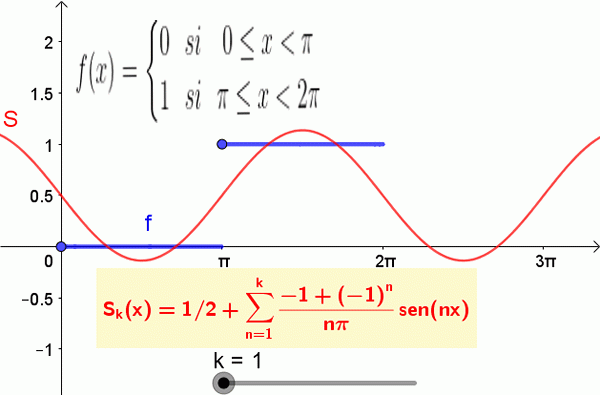Gambar 2. 19 istilah pertama dari jumlah Fourier yang sesuai dengan fungsi langkah ditampilkan. Sumber: f. Zapata.

Penentuan koefisien

Di bawah ini adalah cara menentukan koefisien Fourier:

Misalkan fungsinya adalah f (x) yang didefinisikan dalam interval yang berubah dari t_yo untuk t_yo + T, di mana modal akan menjadi periode fungsi. Maka seri Fourier -nya adalah:

f (t) = a₀/2 + a₁ cos (Ω t) + a₂ cos (2 Ω t) + ... + a_N Cos (n Ω t) +…

.. .+ b₁ sin (Ω t) +b₂ sin (2 Ω t) +... +b_N Sin (n Ω t) +..

Perhitungan istilah independen

Untuk menemukan istilah independen, kami mengintegrasikan kedua anggota kesetaraan dalam interval definisi fungsi:

[T_yo , T_yo+ T]

Karena itu:

Sama_N ∫cos (n Ω t) dt +…

.. .+ b₁ ∫sen (Ω t) dt +b₂ ∫sen (2 Ω t) dt +... +b_N ∫Sen (n Ω t) dt +…

Di sini simbol ∫ berarti integral yang didefinisikan dari T_yo untuk t_yo + T.

Integral dari istilah pertama adalah T, yang ketika dievaluasi dalam hasil batas atasnya:

T_yo + T

Saat mengurangi batas bawah T_yo, dalam t definitif.

Semua istilah lainnya adalah 0, karena ini adalah fungsi kosinus atau sinus yang dievaluasi dalam periode penuh, seperti yang kami tunjukkan di bawah ini:

∫cos (nΩ t) dt = (1/ nΩ) ∫cos (nΩ t) d (nΩ t)

Ingatlah bahwa simbol ∫ berarti integrasi antara t_yo untuk t_yo + T. 

Untuk membuat integrasi istilah yang memiliki kosinus atau payudara kita akan membuat perubahan variabel berikut:

x = Ω (t - t_yo)

Jadi diferensial x, dx sama dengan diferensial d (ωt).

Jadi integral yang harus dilakukan adalah:

Karena n adalah bilangan bulat, maka integral yang ditentukan akan selalu memberikan nol. Hal yang sama berlaku untuk fungsi sinus.

Oleh karena itu, integral yang didefinisikan dievaluasi dalam periode lengkap dari semua istilah yang berisi. 

Dapat melayani Anda: divisi di mana residu 300

Oleh karena itu disimpulkan bahwa istilah A₀ dihitung sebagai berikut:

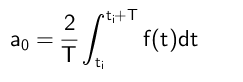
Perhitungan koefisien untuk

Untuk menghitung koefisien yang berlipat ganda dengan fungsi kosinus, kedua anggota kesetaraan harus dikalikan:

f (t) = a₀/2 + a₁ cos (Ω t) + a₂ cos (2 Ω t) + ... + a_N Cos (n Ω t) +…

.. .+ b₁ sin (Ω t) +b₂ sin (2 Ω t) +... +b_N Sin (n Ω t) +..

Oleh fungsi kosinus yang dievaluasi dalam harmonik yang sesuai dan kemudian integral yang didefinisikan dalam periode penuh untuk kedua anggota diterapkan. 

Misalnya, untuk menghitung_M Kedua anggota dikalikan dengan cos (mΩt):

f (t) cos (m Ω t) = a₀/2 cos (m Ω t) + a₁ cos (Ω t) cos (m Ω t) + a₂ cos (2 Ω t) cos (m Ω t) + ... + ke_N Cos (n Ω t) cos (m Ω t) +…

.. .+ b₁ sin (Ω t) cos (m Ω t) +b₂ sin (2 Ω t) cos (m Ω t) +... +b_N Sin (n Ω t) cos (m Ω t) +..

Kemudian berintegrasi ke dalam periode yang lengkap, yaitu, dalam interval yang berubah dari T_yo untuk t_yo + T.

Integral dari istilah yang mengandung A₀ dibatalkan, karena m adalah bilangan bulat dan fungsi kosinus sedang diintegrasikan ke dalam periode penuh. 

Integral yang mengandung produk cos (n Ω t) cos (m Ω t) juga dibatalkan setiap kali n ≠ m. Hanya dalam hal n = m memiliki integral:

Semua istilah yang memiliki sinus berlipat ganda cosinus, yaitu, yang dikalikan dengan koefisien B, seperti yang mengandung integral dari tipe sen (n Ω t) cos (m Ω t) dibatalkan ketika integral yang ditentukan dilakukan pada yang lengkap periode. 

Dari sini disimpulkan bahwa:

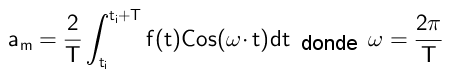
Perhitungan koefisien B

Untuk menemukan koefisien B, prosedur serupa diterapkan, tetapi kali ini kedua anggota fungsi yang cocok dengan seri Fourier dikalikan dengan fungsi SEN (M Ω t).

Untuk alasan yang sama yang sudah dijelaskan untuk kasus di mana satu -satunya istilah yang tidak dibatalkan setelah berintegrasi ke dalam periode yang lengkap adalah di mana:

n = m

Dan di mana integral [sen (m Ω t)] muncul]², yang terintegrasi pada periode yang lengkap menghasilkan π.

Dapat melayani Anda: fungsi homografi: cara grafik, latihan terpecahkan

Dengan cara ini, koefisien B dihitung sesuai dengan formula berikut:

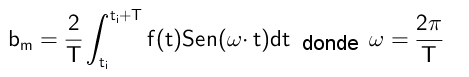
Latihan

- Latihan 1

Membuat perhitungan eksplisit koefisien fungsi

 f (t) = 0 ya 0 ≤ t  < π y 1 si π ≤  t   < 2π

Larutan

Pertama, kami mengidentifikasi periode t fungsi ini sebagai 2π, sehingga frekuensi fundamental Ω = 2π/ t Dalam contoh ini sama dengan unit, yaitu:

Ω = 1

Fungsi didefinisikan dalam interval [0, 2π], sehingga semua integrasi akan dilakukan dalam interval tersebut. 

Maka istilah independen dihitung sebagai berikut:

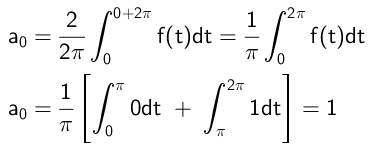
Koefisien yang melipatgandakan fungsi kosinus dihitung dengan cara ini:

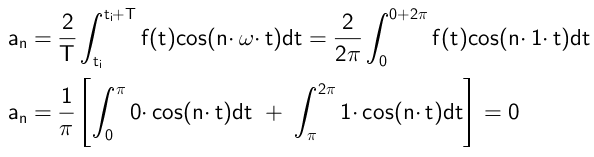
Seperti dapat dilihat, semua koefisien untuk adalah nol, yang akan terjadi dengan ketentuan bahwa fungsi f (t) aneh.

Demikian pula, koefisien B akan dihitung sebagai berikut:

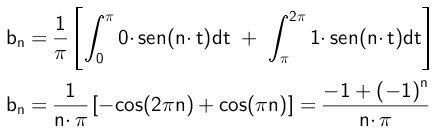
- Latihan 2

Temukan koefisien fungsi yang sesuai dengan Gambar 1, yaitu:

f (t) = -1 ya 0≤ t

Larutan 

Karena fungsi mengambil nilai antara -1 dan +1, kita dapat intuit bahwa istilah independen tidak berlaku, namun kita akan secara eksplisit menghitungnya:

Karena fakta bahwa fungsi tersebut memiliki simetri yang aneh, semua koefisien untuk melipatgandakan istilah harmonik dengan fungsi cosinus harus batal. Kami memverifikasi di bawah ini:

Akhirnya, kita akan menemukan koefisien B yang melipatgandakan istilah harmonik yang berisi fungsi sinus:

Di mana semua istilah B dengan subscript up diperhatikan adalah 0. Istilah aneh pertama adalah:

B₁= -4/(π); B₃= -4/(3π); B₅= -4/(5π); B₇= -4/(7π) dan b₉= -4/(9π)

https: // youtu.Be/737yagwszya

Referensi

1. Amerror, i. 2013. Menguasai Transformasi Fourier Discrete dalam satu, dua atau beberapa dimensi: jebakan dan artefak. Sains Springer & Media Bisnis.
2. Briggs, w. sembilan belas sembilan puluh lima. DFT: Manual Pemilik untuk Transformasi Fourier Discrete. Siam.
3. Chu, e. 2008. Transformasi Fourier Diskrit dan Berkelanjutan: Analisis, Aplikasi dan Algoritma Cepat. CRC Press.
4. Guoan Bi, Yonghong Zeng. 2012. Mengubah dan algoritma cepat untuk analisis dan representasi sinyal. Sains Springer & Media Bisnis.
5. Sundararajan, d. 2003. Pemrosesan Sinyal Digital: Teori dan Praktek.Ilmiah Dunia. 
6. Wikipedia. Seri Fourier. Pulih dari: is.Wikipedia.com