Volume Revolusi Padatan, Jenis, Latihan Terpecahkan

Dia Revolusi solid Ini adalah sosok tiga dimensi yang dihasilkan oleh rotasi permukaan datar di sekitar sumbu aksial atau sumbu revolusi. Gambar 1 menunjukkan animasi revolusi yang dihasilkan dengan cara ini.

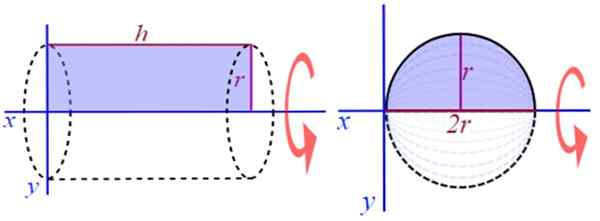
Contoh lain yang sangat mudah untuk divisualisasikan adalah menghasilkan silinder melingkar lurus, memutar persegi panjang dengan tinggi atau panjang H dan Radio R, di sekitar sumbu X positif (Gambar 2). Untuk menemukan volumenya ada formula yang terkenal:

V = Area dasar x tinggi

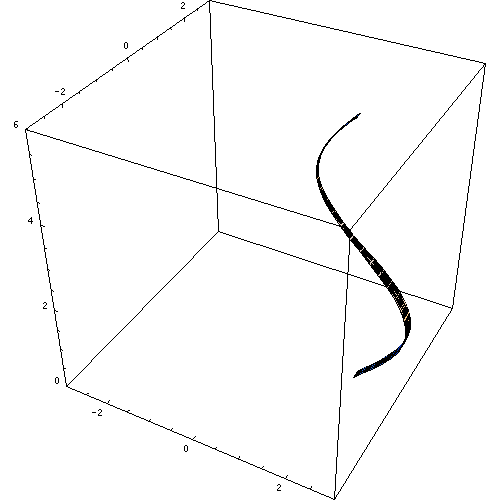Gambar 1. Gambar yang dihasilkan oleh rotasi kurva SEN X. Sumber: Wikimedia Commons. Macks/cc by-sa (https: // createveCommons.Org/lisensi/by-sa/2.5).

Padatan revolusi lainnya adalah bola, kerucut melingkar lurus dan berbagai sosok, sesuai dengan permukaan yang ditempatkan secara rotasi dan tentu saja, sumbu yang dipilih.

Gambar 2. Generasi silinder melingkar lurus dan bola. Sumber: Wikimedia Commons.

Misalnya, memutar setengah lingkaran di sekitar garis yang sejajar dengan diameter revolusi berongga diperoleh.

Untuk silinder, kerucut, bola, baik massa dan lubang, ada formula untuk menemukan volume, yang tergantung pada jari -jari dan tinggi. Tetapi ketika dihasilkan oleh permukaan lain, volume dihitung dengan integral yang ditentukan.

[TOC]

Jenis Revolusi Padatan

Revolusi padatan dapat diklasifikasikan sesuai dengan kurva yang menghasilkannya:

Bola

Itu cukup untuk memutar setengah lingkaran di sekitar sumbu yang akan menjadi diameter radio radio. Volumenya adalah:

V_bola = (4/3) πr³

Cat

Untuk mendapatkan kerucut H dan Radio, permukaan yang harus. Volumenya adalah:

V_Cat = (1/3) πhr²

Silinder

Memutar persegi panjang di sekitar sumbu aksial yang melewati satu sisi, yang bisa menjadi sisi pendek atau sisi panjang, silinder melingkar lurus jari -jari R dan tinggi H diperoleh, yang volumenya adalah:

Dapat melayani Anda: tali (geometri): panjang, teorema dan latihan

V_silinder = πr²H

Toroid

Banteng memiliki bentuk donat. Itu diperoleh dengan memutar daerah melingkar di sekitar garis di bidang yang tidak memotong lingkaran. Volumenya diberikan oleh:

V_Toroid = 2πa²R

Di mana A adalah jari -jari penampang dan R adalah jari -jari toroid sesuai dengan skema yang disajikan pada gambar:

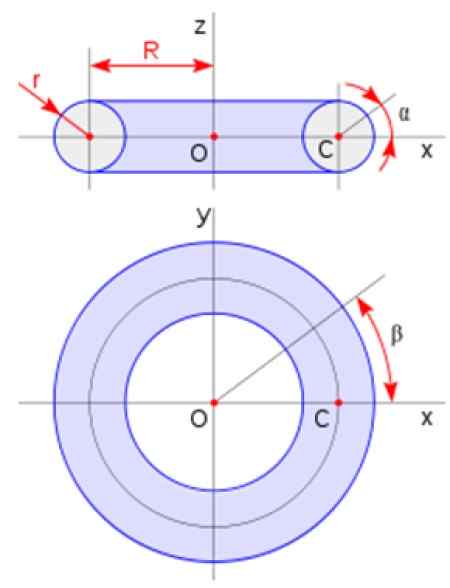Gambar 3. Dimensi toroid. Sumber: Wikimedia Commons.

Metode untuk menghitung volume revolusi yang solid

Dalam perhitungan integral, kedua metode ini sering:

-Cakram dan mesin cuci

-Kerang

Metode disk atau mesin cuci

Saat mengiris revolusi yang solid, penampang bisa berupa album, jika padatan itu padat atau bisa menjadi semacam mesin cuci (album dengan lubang di tengah), jika itu lubang padat.

Misalkan daerah datar diputar di sekitar sumbu horizontal. Dari daerah datar itu kami mengambil persegi panjang Δx kecil, yang diputar secara tegak lurus di sekitar sumbu aksial.

Ketinggian persegi panjang adalah antara kurva terluar r (x) dan r (x) paling internal. Mereka masing -masing sesuai dengan jari -jari eksternal dan radio internal.

Saat membuat rotasi ini, mesin cuci volume ΔV dihasilkan, diberikan oleh:

ΔV = volume penuh - volume lubang (jika ada)

Mengingat bahwa volume silinder melingkar lurus adalah π. radio² x tinggi, kami punya:

ΔV = π [r²(x) - r²(x)] Δx

Padatan dapat dibagi menjadi banyak porsi kecil volume ΔV. Jika kami menambahkan semuanya, kami akan memiliki volume penuh.

Untuk melakukan ini kita akan cenderung 0 volume ΔV, yang juga menjadi sangat kecil, menjadi diferensial DX.

Ini dapat melayani Anda: Acara yang tidak eksklusif: properti dan contoh

Jadi kami memiliki integral:

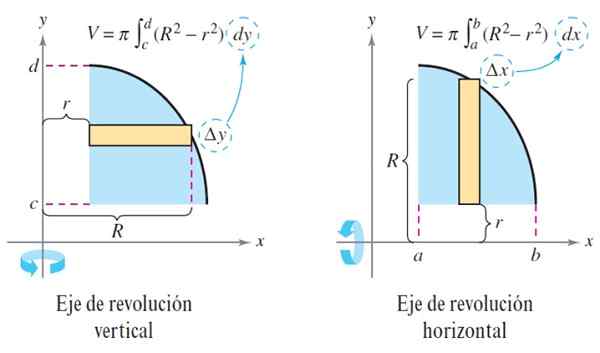
V = ∫_ke^B π [r²(x) - r²(x)] dx

Gambar 3. Metode pencuci. Sumber: Larson. R. Perhitungan.

Jika padatan itu padat, maka fungsi r (x) = 0, irisan padatan yang dihasilkan adalah disk dan volume tetap:

V = ∫_ke^B πr²(x) dx

Ketika sumbu revolusi vertikal, persamaan sebelumnya mengambil bentuk:

V = ∫_ke^B π [r² (Y) - r² (y)] dy dan v = ∫_ke^B πr²(Y) dy

Lapisan

Seperti namanya, metode ini adalah untuk berasumsi bahwa padatan terdiri dari lapisan tebal diferensial. Lapisan adalah tabung tipis yang berasal dari pergantian persegi panjang secara paralel dengan sumbu rotasi.

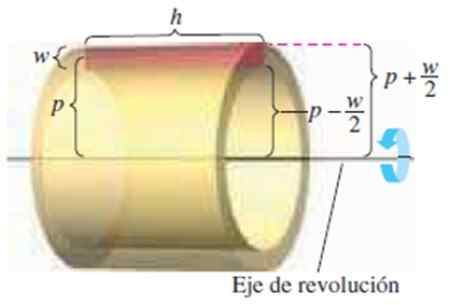Gambar 4. Lapisan silindris tinggi 2, panjang h dan jari -jari p. Sumber: Larson, R. Perhitungan.

Kami memiliki dimensi berikut:

-Ketinggian persegi panjang W

-Bujurnya H

-Jarak dari pusat persegi panjang ke sumbu rotasi P

Mengetahui bahwa volume lapisan itu Volume Luar Ruang - Volume Interior:

π (p + w/2)²H - π (p - w/2)²H

Saat mengembangkan produk terkenal dan menyederhanakan, itu diperoleh:

Volume Lapisan = 2πingkan

Sekarang mari kita buat ketinggian W dari persegi panjang Δy, seperti yang terlihat pada gambar berikut:

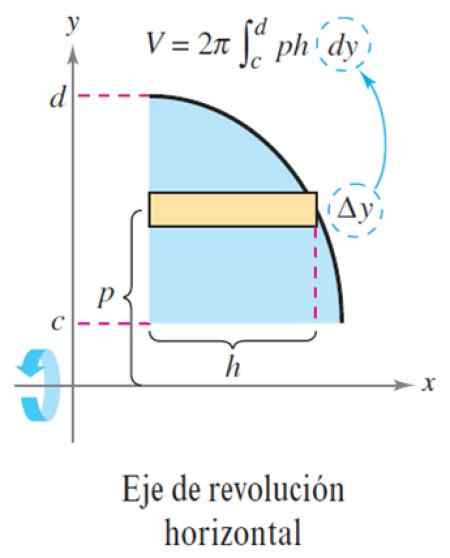Gambar 5. Metode Lapisan Sumbu Revolusi Horizontal. Sumber: Larson, R. Perhitungan variabel.

Dengan ini volume ΔV adalah:

ΔV = 2π p x h x Δy

Dan membuat jumlah lapisan N Jadilah sangat besar, Δy menjadi diferensial dy, sehingga volume total adalah integral:

V = ∫_C^D 2π p (y) h (y) dy

Prosedur yang dijelaskan diterapkan dengan cara yang sama ketika sumbu revolusi vertikal:

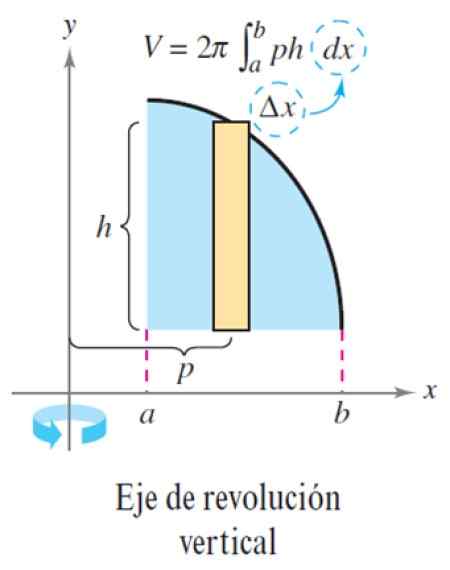Gambar 6. Metode Lapisan untuk Sumbu Revolusi Vertikal. Sumber: Larson, R. Perhitungan variabel.

Olahraga diselesaikan

Temukan volume yang dihasilkan oleh rotasi daerah datar di antara kurva:

y = x²;  y = 0; x = 2

Di sekitar poros dan.

Dapat melayani Anda: homotecia negatif

Larutan

-Hal pertama yang harus dilakukan adalah grafik wilayah yang akan menghasilkan revolusi solid dan menunjukkan poros belokan. Kami memilikinya di grafik berikut:

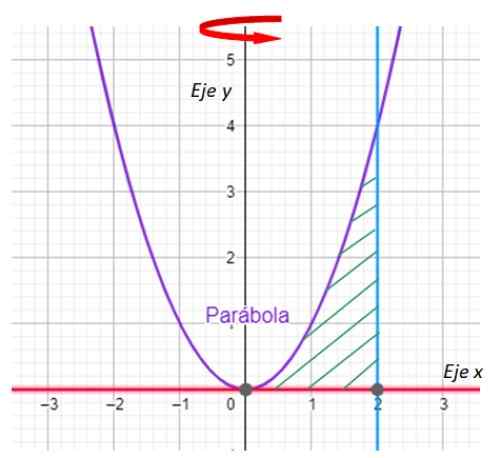Gambar 7. Grafik kurva untuk latihan diselesaikan. Sumber: f. Zapata dengan Geogebra.

-Sekarang persimpangan antara kurva y = x dicari² dan garis x = 2. Untuk bagiannya garis y = 0 tidak lain adalah sumbu x.

Mudah untuk memperingatkan bahwa perumpamaan dan garis berpotongan pada titik (2,4), yang dikuatkan dengan mengganti x = 2 pada y = x².

-Kemudian salah satu metode untuk menghitung volume dipilih, misalnya metode lapisan dengan sumbu revolusi vertikal:

V = ∫_ke^B 2π p (x) h (x) dx

Langkah 1: Gambar persegi panjang

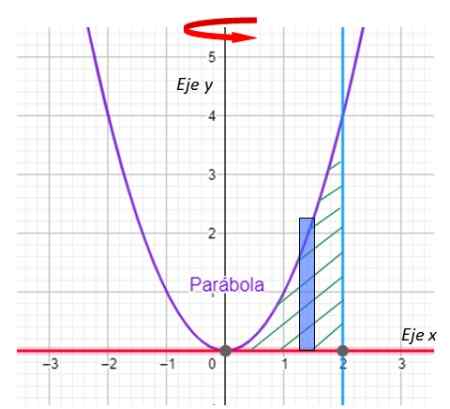Angka 8. Persegi panjang untuk contoh terpecahkan. Sumber: f. Zapata dengan Geogebra.

Penting: Dalam metode layer, sisi panjang persegi panjang sejajar dengan sumbu rotasi.

Langkah 2: Tentukan P (x)

Lapisan lapisan X

Langkah 3: Tentukan h (x)

Ketinggian persegi panjang ditentukan oleh perumpamaan x².

Langkah 4: Membangun dan menyelesaikan integral volume

Variabel integrasi adalah x, yang bervariasi antara 0 dan 2, dengan ini kami memiliki batas integrasi. Mengganti ekspresi untuk p (x) dan h (x)

 Beberapa latihan dapat diselesaikan dengan kedua metode. Dapatkah pembaca memecahkan ini dengan metode pencuci?

Referensi

1. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
2. Purcell, e. 2007. Perhitungan dengan geometri analitik. 9NA. Edisi. Pendidikan Pearson.
3. Wikipedia. Solid revolusi. Diperoleh dari: di.Wikipedia.org.
4. Wikipedia. Toroid. Pulih dari: is.Wikipedia.org.
5. Wolfram Mathworld. Solid revolusi. Dipulihkan dari: MathWorld.Wolfram.com.