Jumlah polinomial, seperti yang dilakukan, contoh, latihan

Itu Jumlah polinomial Operasi yang terdiri dari menambahkan dua atau lebih polinomial, menghasilkan polinomial lain. Untuk melaksanakannya, perlu untuk menambahkan ketentuan dari urutan yang sama dari masing -masing polinomial dan menunjukkan jumlah yang dihasilkan.

Pertama, kami meninjau secara singkat arti "ketentuan dari urutan yang sama". Polinomial siapa pun terdiri dari jumlah dan/atau pengurangan istilah.

Gambar 1. Untuk menambahkan dua polinomial, perlu memesannya dan kemudian mengurangi persyaratan yang sama. Sumber: Pixabay + Wikimedia Commons.

Istilah dapat berupa produk dari bilangan real dan satu atau lebih variabel, diwakili dengan huruf, misalnya: 3x² dan -√5.ke²Bc³ Mereka adalah istilah.

Nah, ketentuan dari urutan yang sama adalah yang memiliki eksponen atau kekuatan yang sama, meskipun mereka mungkin memiliki koefisien yang berbeda.

-Ketentuan urutan yang sama adalah: 5x³, √2 x³ dan -1/2x³

-Istilah pesanan yang berbeda: -2x^-2, 2xy^-1 dan √6x²Dan

Penting untuk diingat bahwa hanya persyaratan dari urutan yang sama yang dapat ditambahkan atau dikurangi, operasi yang dikenal sebagai pengurangan. Kalau tidak, jumlah itu hanya ditunjukkan.

Setelah konsep ketentuan dari urutan yang sama diklarifikasi, polinomial ditambahkan mengikuti langkah -langkah ini:

-Memesan Pertama polinomial yang ditambahkan, semuanya dengan cara yang sama, baik meningkat atau menurun, yaitu, dengan kekuatan dari paling sedikit ke terbesar atau sebaliknya.

-Untuk menyelesaikan, Jika ada kekuatan dalam urutan yang hilang.

-Mengurangi Istilah yang sama.

-Menunjukkan Jumlah yang dihasilkan.

[TOC]

Contoh jumlah polinomial

Kami akan mulai dengan menambahkan dua polinomial dengan satu variabel yang disebut X, Misalnya polinomial p (x) dan q (x) yang diberikan oleh:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Mengikuti langkah -langkah yang dijelaskan, itu dimulai dengan memesannya dengan menurun, yang merupakan cara yang paling umum:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Itu dapat melayani Anda: sudut bertuliskan lingkaran: definisi, teorema, contoh

Q (x) = x⁵+ X² - 25x

Polinomial Q (x) tidak lengkap, terlihat bahwa kekuatan dengan eksponen 4, 3 dan 0. Yang terakhir hanyalah istilah independen, yang tidak memiliki surat.

Q (x) = x⁵+ 0x⁴ + 0x³ + X² - 25x + 0

Setelah langkah ini selesai, mereka siap untuk ditambahkan. Anda dapat menambahkan istilah yang sama dan kemudian menunjukkan jumlah, atau menempatkan polinomial yang dipesan satu sama lain dan mengurangi kolom, dengan cara ini:

- X⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ X⁵ + 0x⁴ + 0x³  +  X²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Penting untuk dicatat bahwa ketika ditambahkan, itu dilakukan secara aljabar dengan menghormati aturan tanda, dengan cara ini 2x + (-25 x) = -23x. Yaitu, jika koefisien memiliki tanda yang berbeda dikurangi dan hasilnya membawa tanda mayor.

Tambahkan dua atau lebih polinomial dengan lebih dari satu variabel

Ketika datang ke polinomial dengan lebih dari satu variabel, salah satunya dipilih untuk memesannya. Misalnya, misalkan itu diminta untuk menambahkan:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

DAN:

T (x, y) = ½ x²- 6y²  - 11xy + x³Dan

Salah satu variabel dipilih, misalnya X untuk memesan:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

Ketentuan yang hilang segera selesai, yang dimiliki oleh masing -masing polinomial:

R (x, y) = 0x³dan + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

Dan keduanya siap mengurangi istilah yang sama:

0x³dan + 5x² +  8xy - 6y³  - 4y²

Dapat melayani Anda: koefisien penentuan: rumus, perhitungan, interpretasi, contoh

+ X³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ X³Y + 11/2x² - 3xy - 6y³  - 10y²    = R (x, y) + t (x, y)

Latihan jumlah polinomial

- Latihan 1

Dalam jumlah polinomial berikutnya, tunjukkan istilah yang harus dibiarkan kosong untuk mendapatkan jumlah polinomial:

-5x⁴  + 0x³ +  2x²         + 1

X⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Larutan

Untuk mendapatkan -6x⁵ Istilah formulir kapak diperlukan⁵, seperti yang:

A + 1+ 2 = -6

Karena itu:

A = -6-1-2 = -9

Dan istilah yang dicari adalah:

-9x⁵

-Lanjutkan dengan cara yang sama untuk menemukan sisa persyaratan. Berikut adalah eksponen 4:

-5 + 2 + A = 10 → A = 10 + 5-2 = 13

Istilah yang hilang adalah: 13x⁴.

-Untuk X Powers³ Segera bahwa istilah tersebut harus -9x³, Dengan cara ini koefisien istilah kubik adalah 0.

-Adapun kekuatan kuadrat: A + 8 -14 = -11 → A = -11 -8 + 14 = -5 dan istilah -5x².

-Istilah linier diperoleh dengan +8 -14 = -11 → a = -11 + 14 -8 = -5, menjadi istilah yang hilang -5x.

-Akhirnya, istilah independen adalah: 1 -3 + a = -21 → a = -19.

- Latihan 2

Medan datar dikelilingi seperti yang ditunjukkan pada gambar. Temukan ekspresi untuk:

a) perimeter dan

b) luasnya, dalam hal panjang yang ditunjukkan:

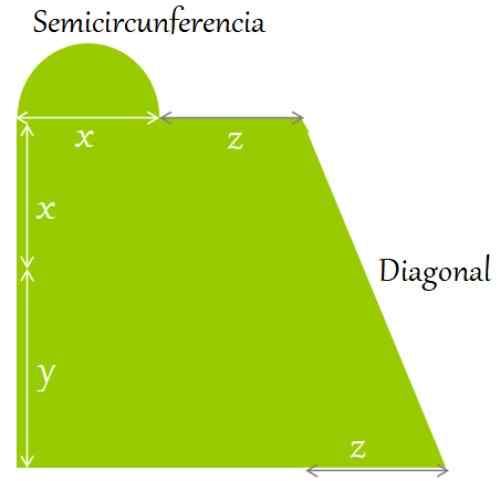Gambar 2. Medan datar dikelilingi oleh bentuk dan dimensi yang ditunjukkan. Sumber: f. Zapata.

Solusi untuk

Perimeter didefinisikan sebagai jumlah sisi dan kontur gambar. Mulai di sudut kiri bawah, ke arah tangan jam, Anda memiliki:

Itu dapat melayani Anda: Isosceles Trapezoid: Properties, Hubungan dan Formula, Contoh

Perimeter = y + x + Panjang setengah lingkaran + z + panjang diagonal + Z + z + x

Setengah lingkaran memiliki diameter sama dengan x. Karena jari -jari itu setengah diameter, ia harus:

Radio = x/2.

Formula untuk panjang lingkar lengkap adalah:

L = 2π x radio

Jadi:

Panjang setengah lingkaran = ½. 2π (x/2) = πx/2

Untuk bagiannya, diagonal dihitung dengan teorema Pythagoras yang diterapkan pada sisi: (x+y) yang merupakan sisi vertikal dan z, yang merupakan horizontal:

Diagonal = [(x+y)² + z²]^1/2

Ekspresi ini diganti dalam perimeter, untuk mendapatkan:

Perimeter = y + x + πx/2 + z + [(x + y)² + z²]^1/2+ z + x + z

Istilah serupa dikurangi, karena jumlah mensyaratkan bahwa hasilnya disederhanakan hingga maksimum:

Perimeter = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z²]^1/2 = y + (2 + π /2) x + 3z

Solusi b

Area yang dihasilkan adalah jumlah area persegi panjang, setengah lingkaran dan segitiga kanan. Rumus untuk area ini adalah:

-Persegi panjang: Dasar X Tinggi

-Setengah lingkaran: ½ π (radio)²

-Segi tiga: Basis x tinggi /2

Area persegi panjang

(x+y). (x+z) = x² + Xz + yx + yz

Area setengah lingkaran

½ π (x/2)² = π x² / 8

Area segitiga

½ z (x + y) = ½ zx + ½ zy

Area Total

Untuk menemukan total area, ekspresi yang ditemukan untuk setiap area parsial ditambahkan:

Total Area = X² + Xz + yx + yz + (π x² / 8) + ½ zx + ½ zy

Dan akhirnya semua istilah yang serupa:

Total Area = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Referensi

1. Baldor, a. 1991. Aljabar. Editorial Budaya Venezuela S.KE.
2. Jiménez, r. 2008. Aljabar. Prentice Hall.
3. Matematika itu menyenangkan. Menambahkan dan pengurangan polinomial. Pulih dari: mathsisfun.com.
4. Institut Monterey. Menambahkan dan Mengurangi Polinomial. Pulih dari: montereyinstitute.org.
5. UC Berkeley. Aljabar polinomial. Pulih dari: matematika.Berkeley.Edu.