Jumlah metode grafik vektor, contoh, latihan terpecahkan

Itu jumlah vektor Ini adalah operasi tambahan antara vektor yang menghasilkan vektor lain. Vektor ditandai dengan memiliki besarnya, dan juga arah dan makna. Oleh karena itu tidak mungkin, secara umum, menambahkannya seperti yang akan dilakukan dengan jumlah skalar, yaitu, menambahkan angka.

Vektor yang diperoleh dari jumlah beberapa vektor disebut vektor yang dihasilkan. Dalam mekanik kita berbicara tentang kekuatan yang dihasilkan, yang merupakan jumlah vektor dari semua kekuatan pada tubuh. Hasil ini setara dengan himpunan atau sistem kekuatan.

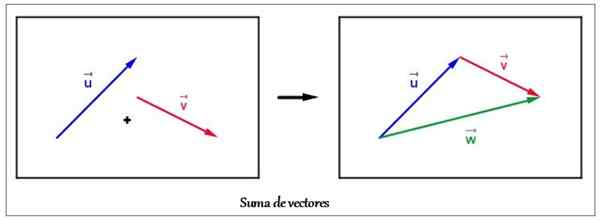
Untuk sepenuhnya menentukan jumlah vektor, perlu untuk menunjukkan besarnya dan persatuan, arah dan makna.

Penting untuk menyoroti bahwa dengan menambahkan vektor, ini harus mewakili besarnya fisik yang sama, oleh karena itu jumlah vektor adalah operasi yang homogen. Ini berarti bahwa kita dapat menambahkan satu kekuatan dengan yang lain, tetapi bukan kekuatan dengan perpindahan, karena hasilnya tidak berarti.

Beberapa metode tersedia untuk menemukan vektor yang dihasilkan: grafik dan analitik. Untuk menemukan jumlah vektor dengan metode grafis, ini didasarkan pada representasi sederhana untuk vektor, yaitu, segmen berorientasi atau panah seperti ini:

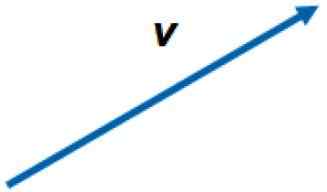Representasi grafis vektor di pesawat. Sumber: f. Zapata.

Vektor dilambangkan dengan huruf hitam dalam teks cetak, atau dengan panah di atas surat itu, untuk membedakannya dari magnitudo masing -masing atau jumlah skalarnya. Misalnya, besarnya vektor v Itu sederhana v.

[TOC]

Metode grafis untuk menambahkan vektor

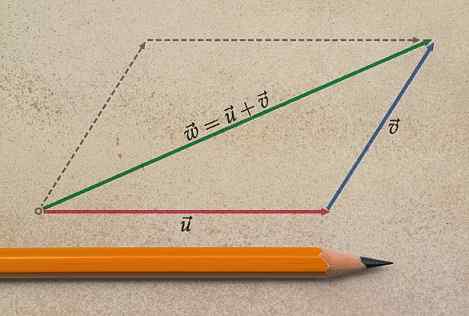
Untuk menambahkan lebih dari dua vektor bait, Metode poligon salah satu poligon, yang terdiri dari mentransfer diri ke masing -masing vektor yang diatasi. Karakteristik dari vektor adalah bahwa mereka invarian tentang terjemahan, oleh karena itu kami akan menggunakan properti ini untuk menetapkan jumlah.

Dapat melayani Anda: pelebaran termal

Itu dimulai dengan salah satu vektor, karena penambahan vektor bersifat komutatif dan urutan penambahan tidak mengubah jumlah. Vektor kedua bergerak di bawah, cocok dengan asalnya dengan akhir yang pertama.

Kemudian dibawa ke vektor berikutnya dan kemudian menempatkan prosedur yang sama, yaitu untuk mencocokkan asal dengan akhir yang sebelumnya. Kami melanjutkan dengan cara ini untuk memposisikan vektor terakhir.

Vektor yang dihasilkan adalah yang bergabung dengan asal yang pertama dengan ujung bebas yang terakhir. Nama metode ini berasal dari gambar yang dihasilkan: poligon.

Contoh

Jumlah contoh dua vektor dalam bidang dengan metode grafik. Sumber: Wikimedia Commons

Mari kita ambil contoh jumlah dari dua vektor atau Dan v yang ditunjukkan pada gambar atas.

Dimulai dengan vektor atau, Dia pindah ke vektor v Untuk mencocokkan asalnya dengan akhir yang pertama. Vektor yang dihasilkan W Itu diambil dari asal atau sampai akhir v, Membentuk angka tiga -sisi: segitiga. Itulah sebabnya dalam kasus khusus ini, prosedur ini disebut Metode segitiga.

Perhatikan detail penting, besarnya atau modul dari vektor yang dihasilkan bukanlah jumlah modul vektor tambahan. Faktanya, hampir selalu kurang, kecuali vektornya paralel.

Mari kita lihat di bawah apa yang terjadi dalam kasus ini.

Kasus Khusus: Jumlah Vektor Paralel

Metode yang dijelaskan juga dapat diterapkan pada kasus khusus di mana vektor paralel. Pertimbangkan contoh berikut:

Dapat melayani Anda: Boltzmann Constant: Sejarah, Persamaan, Perhitungan, LatihanJumlah vektor paralel. Sumber: f. Zapata.

Vektor dibiarkan v Dalam posisi semula, dan pindah ke vektor atau sedemikian rupa sehingga asalnya setuju dengan akhir  v. Sekarang vektor diambil dari asal v Dan akhir atau.

Ini adalah vektor yang dihasilkan W dan ukurannya adalah jumlah ukuran iklan. Arah dan arah dari tiga vektor adalah sama.

Vektor yang dihasilkan memiliki modul maksimum jika addors membentuk sudut 0º, seperti contoh dari contoh. Jika vektor membentuk sudut 180º dengan satu sama lain, maka vektor yang dihasilkan memiliki modul minimum.

Contoh jumlah vektor

- Perpindahan

Seorang pengendara sepeda melakukan perjalanan 3 km pertama menuju utara dan kemudian 4 km barat. Perpindahan Anda, yang kami sebut R, Ini mudah ditemukan dengan metode segitiga ditambah sistem referensi, di mana titik -titik kardinal ditandai:

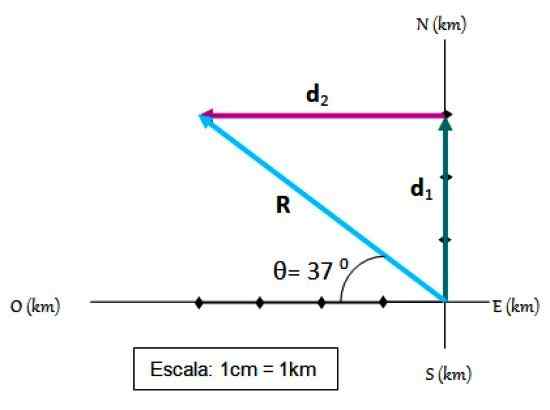Dihasilkan dari dua perpindahan. Sumber: f. Zapata.

Langkah untuk Menambahkan Vektor

-Titik awal bertepatan dengan asal sistem referensi.

-Pada sumbu koordinat, skala dipilih, yang dalam hal ini adalah 1 cm = 1 km

-Perpindahan pertama ditarik pada skala D_1.

-Lalu a D₁ Perpindahan kedua ditarik D₂, Juga pada skala.

-Perpindahan yang dihasilkan R Itu adalah vektor yang beralih dari asal ke akhir D₂.

-Ukuran dari R Ini diukur dengan aturan lulus, mudah untuk memverifikasi bahwa r = 5.

-Akhirnya sudut itu R Bentuk dengan horizontal diukur dengan bantuan transporter dan ternyata θ = 37 ⁰

- Kecepatan yang dihasilkan

Seorang perenang ingin menyeberangi sungai dan tidak ada apa -apa dengan kecepatan 6 km/jam, tegak lurus ke pantai, tetapi arus yang membawa kecepatan 4 km/jam menyimpang.

Itu dapat melayani Anda: ohm: tindakan resistensi, contoh dan olahraga diselesaikan

Untuk mengetahui kecepatan yang dihasilkan, vektor kecepatan perenang ditambahkan, yang telah ditarik vertikal dan arus, yang horizontal.

Mengikuti metode grafik kecepatan yang dihasilkan diperoleh v_R:

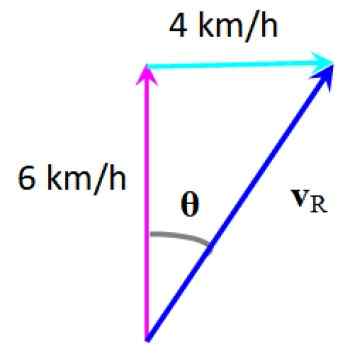Kecepatan yang dihasilkan. Sumber: f. Zapata.

Penyimpangan yang dialami oleh perenang dapat dihitung dengan:

θ = arctg (4/6) = 33.7 di sebelah kanan alamat awal Anda

Besarnya kecepatannya meningkat karena kecepatan sungai menambah secara vektor. Anda dapat menemukan skala dengan hati -hati, seperti pada contoh sebelumnya.

Atau dengan bantuan alasan trigonometri 33.7:

Sen 33.7 = 4/v_R

v_R = 4/ sin 33.7 = 7.21 km/jam

Olahraga diselesaikan

Pada sebuah partikel, Undang -Undang Kekuatan berikut, yang besarnya tercantum di bawah ini:

F₁= 2.5 n; F₂= 3 n; F₃= 4 n; F₄= 2.5 n

Temukan kekuatan yang dihasilkan.

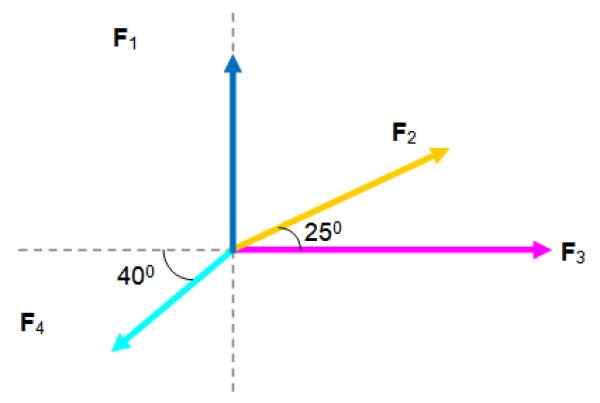Sistem Pasukan Coplanar. Sumber: f. Zapata.

Larutan

Kita dapat menambahkan secara grafis dimulai dengan salah satu vektor, karena jumlah vektor adalah komutatif.

Pada Gambar A dimulai dengan F₁. Membangun skala dan dengan bantuan aturan dan pasukan vektor lain ditransfer untuk menempatkannya satu demi satu.

Vektor F_R diarahkan dari asal F₁ sampai akhir F₄. Besarnya 5.2 N dan membentuk sudut 26.Ke -5 sehubungan dengan horizontal.

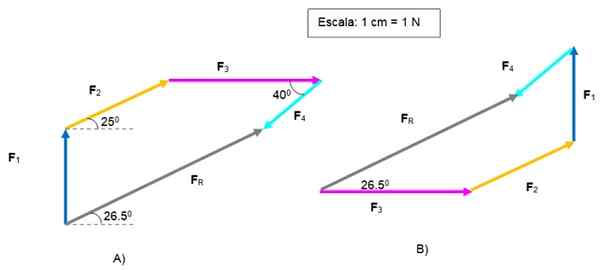Jumlah grafik vektor. Sumber: f. Zapata.

Pada Gambar B, masalah yang sama diselesaikan, dimulai dengan F₃ dan berakhir dengan F₄, Untuk mendapatkan yang sama F_R .

Poligonnya berbeda, tetapi hasilnya sama. Pembaca dapat menguji urutan vektor lagi.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fisika. 2nd. Ed. Bukit McGraw.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.