Contoh metode jajaran genjang, latihan terpecahkan

Dia Metode jajaran genjang Ini adalah metode grafis untuk menambahkan dua vektor di pesawat. Ini sering digunakan untuk menemukan hasil dari dua kekuatan yang diterapkan pada tubuh atau dua kecepatan, seperti dalam kasus perenang yang bermaksud melintasi sungai yang tegak lurus dan dialihkan oleh arus.

Untuk membangun jajaran genjang, asal -usul vektor yang akan ditambahkan, ditarik pada skala, harus bertepatan pada suatu titik.

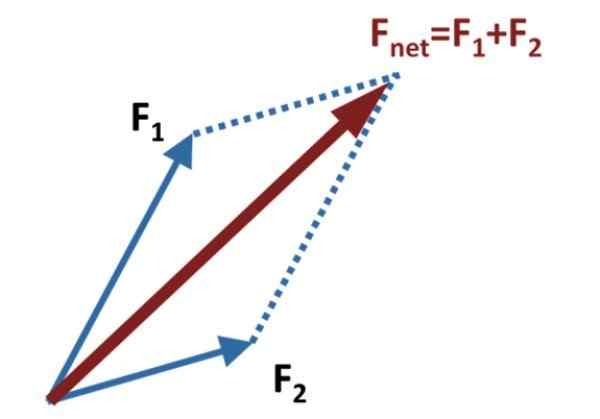
Gambar 1. Metode jajaran genjang untuk menambahkan dua vektor. Sumber: Wikimedia Commons.

Kemudian garis bantu ditarik paralel dengan masing -masing vektor, yang mencapai ujung yang lain, seperti yang ditunjukkan pada gambar atas.

Vektor tambahan atau yang dihasilkan, juga disebut gaya bersih, adalah vektor F_bersih, yang diperoleh dengan menggambar vektor yang berasal dari asal umum F₁ Dan F₂, Ke titik di mana garis paralel tambahan berpotongan. Dalam diagram gambar ini diwakili oleh garis putus -putus.

Metode ini menerima namanya dari gambar yang dibentuk dengan pecandu dan garis tambahan, yang justru jajaran genjang. Diagonal utama jajaran genjang adalah vektor jumlah.

Sangat penting untuk menekankan bahwa urutan vektor tambahan ditempatkan tidak mengubah jumlah, karena operasi antara vektor ini bersifat komutatif.

[TOC]

Contoh metode jajaran genjang langkah demi langkah

Gambar berikut menunjukkan vektor v Dan atau Di unit sewenang -wenang. Vektor v Ukuran 3.61 unit dan membentuk sudut 56.3 dengan horizontal, sementara atau Ukuran 6.32 unit dan sudut 18.4º Mengenai garis referensi ini.

Dapat melayani Anda: Kesalahan acak: rumus dan persamaan, perhitungan, contoh, latihan

Mari kita temukan vektor Anda menambahkan melalui metode jajaran genjang.

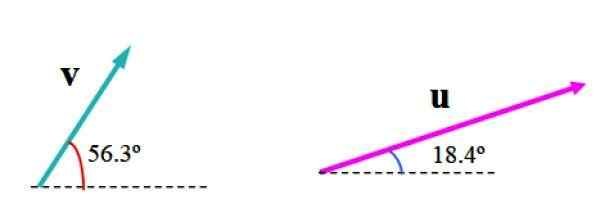Gambar 2. Dua vektor di pesawat, yang kami ingin temukan vektor yang dihasilkan. Sumber: f. Zapata

Perlu untuk memilih skala yang sesuai, seperti yang ditunjukkan pada gambar berikut, di mana pesawat telah dibagi dengan kisi -kisi. Lebar kuadrat mewakili satu (1) unit.

Karena vektor tidak berubah ketika mereka ditransfer, mereka ditempatkan sedemikian rupa sehingga asal mereka bertepatan dengan asal sistem koordinat (gambar kiri).

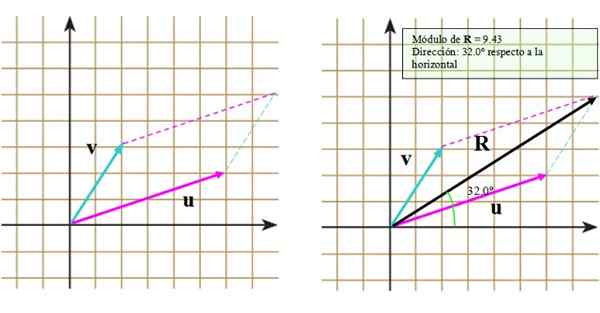Gambar 3. Jumlah vektor melalui metode jajaran genjang. Sumber: f. Zapata.

Sekarang mari kita ikuti langkah -langkah ini:

1. Vektor akhir vektor v Garis tersegmentasi yang sejajar dengan vektor atau.
2. Ulangi prosedurnya tetapi kali ini dengan akhir vektor atau.
3. Gambarlah diagonal utama yang memanjang dari asal umum ke titik persimpangan garis tersegmentasi.

Hasilnya dapat dilihat pada gambar yang tepat, di mana vektor yang dihasilkan muncul R.

Jika kita ingin mengetahui besarnya R, Kita dapat mengukur panjangnya dan membandingkannya dengan skala yang kita miliki. Dan untuk arah mereka, sumbu horizontal atau sumbu vertikal dapat digunakan sebagai referensi, misalnya.

Dengan menggunakan sumbu horizontal atau sumbu x, sudut itu R Bentuk dengan sumbu ini diukur dengan konveyor dan dengan cara ini kita tahu alamatnya R.

Juga, besarnya dan arah R Mereka dapat dihitung dengan teorema kosinus dan payudara, karena jajaran genjang yang terbentuk dapat dibagi menjadi dua segitiga kongruen, yang sisinya adalah modul dari vektor atau, v Dan R. Lihat contoh diselesaikan 1.

Dapat melayani Anda: kecepatan instan: definisi, formula, perhitungan dan latihan

Kasus Khusus: Jumlah vektor tegak lurus

Ketika vektor saling tegak lurus, gambar yang terbentuk adalah persegi panjang. Modul vektor yang dihasilkan sesuai dengan panjang diagonal, yang dapat dengan mudah dihitung dengan teorema Pythagoras.

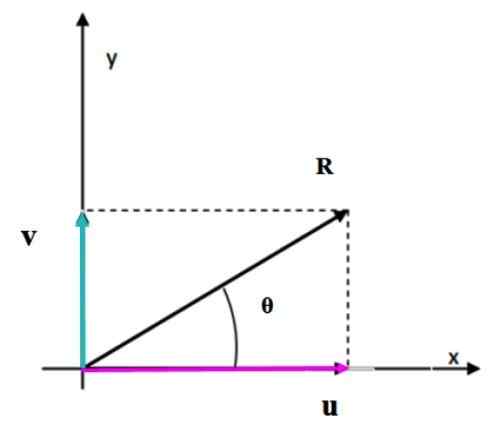Gambar 4. Jumlah dua vektor tegak lurus menggunakan metode jajaran genjang. Sumber: f. Zapata.

Latihan terpecahkan

- Latihan 1

Anda memiliki vektor v, Ukuran mana 3.61 unit dan membentuk sudut 56.3 dengan horizontal, dan vektor atau, yang ukurannya 6.32 unit dan membentuk sudut 18.4 (Gambar 2). Tentukan modul vektor yang dihasilkan R = atau + v dan arah yang membentuk vektor tersebut dengan sumbu horizontal.

Larutan

Metode jajaran genjang diterapkan sesuai dengan langkah -langkah yang dijelaskan di atas, untuk mendapatkan vektor R. Seperti yang dinyatakan sebelumnya, jika vektor ditarik dengan hati -hati mengikuti skala dan menggunakan aturan dan transporter, besarnya dan arah R Mereka diukur langsung pada gambar.

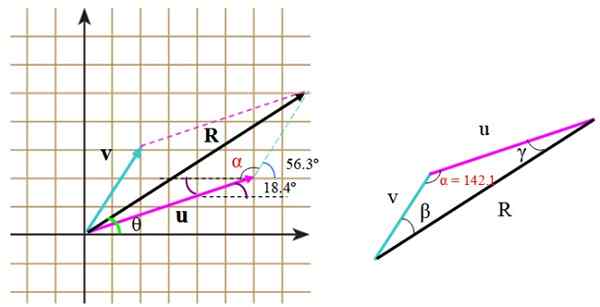Gambar 5.- Perhitungan besarnya dan arah vektor yang dihasilkan. Sumber: f. Zapata.

Mereka juga dapat dihitung secara langsung, dengan bantuan trigonometri dan sifat -sifat sudut. Ketika segitiga terbentuk bukan persegi panjang, seperti dalam kasus ini, teorema kosinus diterapkan untuk menemukan sisi yang hilang.

Di segitiga kanan, sisi mengukur u, v dan r. Untuk menerapkan teorema kosinus, perlu mengetahui sudut di antara v Dan atau, yang dapat kita temukan dengan bantuan kisi, memposisikan sudut yang dipasok dengan benar oleh pernyataan itu.

Sudut ini α dan terdiri dari:

α = (90-56.3) + 90º +18.4 = 142.1st

Dapat melayani Anda: Dwarf merah

Menurut Teorema Coseno:

R² = v² + atau² - 2u⋅v⋅cos α = 3.61² + 6.32² - 23.61 × 6.32 × cos 142.1 = 88.98

R = 9.43 unit.

Akhirnya, sudut antara R Dan sumbu horizontal adalah θ = 18.4 º + γ. Sudut γ dapat ditemukan dengan teorema payudara:

sin α / r = sen γ / u

Karena itu:

sin γ = v (sin α / r) = 3.61 x (sen 142.1 /9.43)

γ = 13.6

θ = 18.4 º + 13.6 º = 32º

- Latihan 2

Seorang perenang bersiap untuk melintasi renang sungai secara tegak lurus dengan arus dengan kecepatan konstan 2.0 m/s. Perenang mulai dari A, namun berakhir dengan B, titik hilir, karena arus yang mengalihkannya.

Jika kecepatan arus adalah 0.8 m/s dan semua kecepatan seharusnya menemukan kecepatan perenang seperti yang terlihat oleh seorang pengamat yang berdiri di pantai.

Larutan

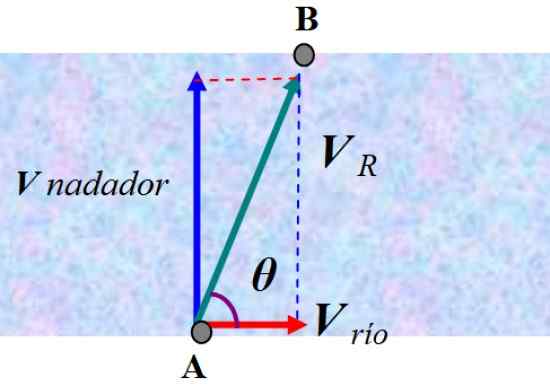Gambar 6. Jumlah kecepatan dengan metode jajaran genjang. Sumber: f. Zapata.

Seorang pengamat yang berdiri di pantai akan melihat bagaimana perenang dialihkan sesuai dengan kecepatan yang dihasilkan V_R. Untuk menemukan jawaban, kita perlu menambahkan kecepatan perenang dan kecepatan arus, yang kita sebut V _sungai:

V _R = V _perenang + V _sungai

Pada gambar, yang tidak ada dalam skala, vektor ditambahkan untuk mendapatkan V _R. Dalam hal ini, teorema Pythagoras dapat diterapkan untuk mendapatkan besarnya:

V_R² = 2.0² + 0.8² = 4.64

V_R = 2.15 m/s

Alamat di mana perenang arah tegak lurus mudah dihitung, memperhatikan bahwa:

θ = arctg (2/0.8) = 68.2nd

Kemudian perenang menyimpang 90º - 68.2 = 27.Ke -2 dari alamat asli Anda.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fisika. 2nd. Ed. Bukit McGraw.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.