Teorema Bolzano

Kami menjelaskan apa itu Teorema Bolzano, aplikasinya dan latihan yang diselesaikan

Apa Teorema Bolzano?

Dia Teorema Bolzano Itu menetapkan bahwa jika suatu fungsi terus menerus pada semua titik interval tertutup [a, b] dan dipenuhi bahwa citra "a" dan "b" (di bawah fungsi) memiliki tanda -tanda yang berlawanan, maka akan ada setidaknya ada satu titik "c" dalam interval terbuka (a, b), sehingga fungsi dievaluasi dalam "c" akan sama dengan 0.

Teorema ini dinyatakan oleh filsuf, teolog dan matematikawan Bernard Bolzano pada tahun 1850. Ilmuwan ini, lahir di Republik Ceko saat ini, adalah salah satu matematika pertama dalam sejarah yang membuat demonstrasi formal sifat -sifat fungsi berkelanjutan.

Penjelasan Teorema

Teorema Bolzano juga dikenal sebagai teorema nilai -nilai menengah, yang membantu dalam menentukan nilai -nilai spesifik, terutama nol, dari fungsi nyata tertentu dari variabel nyata.

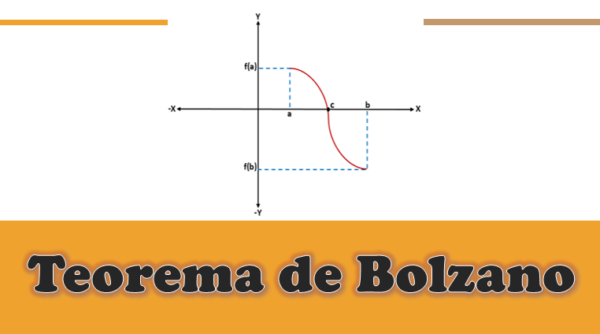
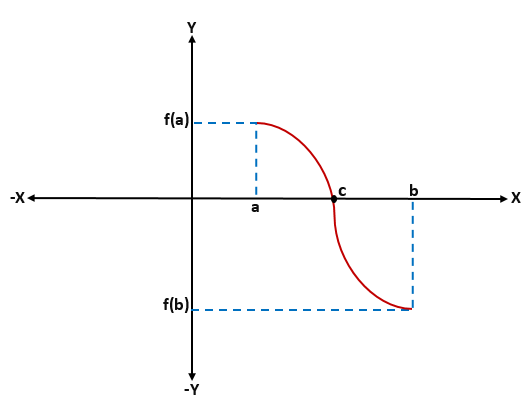
Dalam fungsi yang diberikan f (x) berlanjut -yaitu, bahwa f (a) dan f (b) dihubungkan oleh kurva-, di mana f (a) di bawah sumbu x (negatif), dan f (b) Dengan di atas sumbu x (positif), atau sebaliknya, akan ada titik pemotongan pada sumbu x yang akan mewakili nilai menengah "C", yang akan berada di antara "A" dan "B", dan nilainya dari f (c) akan sama dengan 0.

Saat menganalisis secara grafis teorema Bolzano, dapat diketahui bahwa untuk setiap fungsi F kontinu yang didefinisikan dalam interval [a, b], di mana f (a)_*f (b) kurang dari 0, akan ada setidaknya satu akar "c" dari fungsi itu dalam interval (a, b).

Teorema ini tidak menetapkan jumlah titik yang ada dalam interval terbuka itu, hanya menyatakan bahwa setidaknya ada 1 poin.

Demonstrasi Teorema Bolzano

Untuk menunjukkan teorema Bolzano, diasumsikan tanpa kehilangan umum bahwa f (a) 0; Dengan cara ini, mungkin ada banyak nilai antara "a" dan "b" yang f (x) = 0, tetapi hanya perlu untuk menunjukkan bahwa ada satu.

Dapat melayani Anda: Nomor Imajiner: Properti, Aplikasi, Contoh

Mulai mengevaluasi f di titik tengah (a+b)/2. Jika f ((a+b)/2) = 0 maka tes berakhir di sini; Jika tidak, maka f ((a+b)/2) positif atau negatif.

Salah satu bagian dari interval [a, b] dipilih, sehingga tanda -tanda fungsi yang dievaluasi di ujungnya berbeda. Interval baru ini akan menjadi [A1, B1].

Sekarang, jika F dievaluasi di titik tengah [A1, B1] bukan nol, maka operasi yang sama dilakukan sebelumnya; Yaitu, setengah dari interval ini yang memenuhi kondisi tanda -tanda dipilih. Jadilah interval baru ini [A2, B2].

Jika proses ini berlanjut, maka akan ada dua suksesi an dan bn, sedemikian rupa sehingga:

an tumbuh dan bn berkurang:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Jika panjang setiap interval [AI, BI] dihitung, Anda harus:

B1-a1 = (b-a)/2.

B2-a2 = (b-a)/2².

.. .

bn-an = (b-a)/2^n.

Oleh karena itu, batas ketika n cenderung tak terhingga (bn-an) sama dengan 0.

Menggunakan an tumbuh dan terbatas dan bn menurun dan terbatas, ada nilai "c" sehingga:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. .≤ c ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Batas lim adalah "C" dan batas bn juga "C". Oleh karena itu, diberikan Δ> 0, selalu ada "n" sedemikian rupa sehingga interval [an, bn] terkandung dalam interval (c-δ, c+δ).

Sekarang, harus ditunjukkan bahwa f (c) = 0.

Jika f (c)> 0, maka sebagai f kontinu, ada ε> 0 sehingga f positif di seluruh interval (c -ε, c+ε). Namun, seperti yang dinyatakan di atas, ada nilai "n" sedemikian rupa sehingga f perubahan masuk [an, bn] dan, di samping itu, [an, bn] terkandung dalam (c -ε, c+ε), apa apa adanya apa adanya kontradiksi.

Jika f (c) 0 sedemikian rupa sehingga f negatif sepanjang interval (c -ε, c+ε); Tetapi ada nilai "n" yang diubah F masuk [an, bn]. Ternyata [an, bn] terkandung dalam (c -ε, c+ε), yang juga merupakan kontradiksi.

Dapat melayani Anda: tanda -tanda pengelompokan

Oleh karena itu, f (c) = 0 dan inilah yang ingin ditunjukkan.

Untuk apa Teorema Bolzano?

Dari interpretasi grafisnya, teorema Bolzano digunakan untuk menemukan akar atau nol dalam fungsi kontinu, melalui bisensi (pendekatan), yang merupakan metode pencarian tambahan yang selalu membagi interval menjadi 2.

Dengan demikian, jika fungsi berubah menandatangani interval, fungsi F dievaluasi di titik tengah, yang dinyatakan sebagai berikut: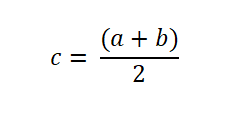Akar ditemukan ketika f (c) = 0. Jika tidak, tanda f (c) dianalisis untuk menentukan apakah itu bertentangan dengan tanda f (a) atau f (b).

Kemudian interval [a, c] atau [c, b] diambil di mana perubahan tanda terjadi, dan proses diulang sampai interval semakin sedikit, untuk mendekati nilai yang Anda inginkan; yaitu nilai yang dilakukan fungsi 0.

Singkatnya, untuk menerapkan teorema Bolzano dan dengan demikian menemukan akar, membatasi nol dari suatu fungsi atau memberikan solusi untuk persamaan, langkah -langkah berikut dilakukan:

1. Diverifikasi jika F adalah fungsi kontinu dalam interval [a, b].
2. Jika interval tidak diberikan, seseorang harus menemukan satu di mana fungsinya kontinu.
3. Itu diverifikasi jika ujung interval memberikan tanda -tanda yang berlawanan ketika dievaluasi di f.
4. Jika tanda -tanda yang berlawanan tidak diperoleh, interval harus dibagi menjadi dua subinterval menggunakan titik tengah.
5. Mengevaluasi fungsi di titik tengah dan memverifikasi bahwa hipotesis bolzano terpenuhi, di mana f (a) _* f (b) < 0.
6. Bergantung pada tanda (positif atau negatif) dari nilai yang ditemukan, proses diulangi dengan subinterval baru sampai hipotesis yang disebutkan terpenuhi.

Dapat melayani Anda: pemrograman non -linier: metode dan latihan

Latihan terpecahkan

Latihan 1

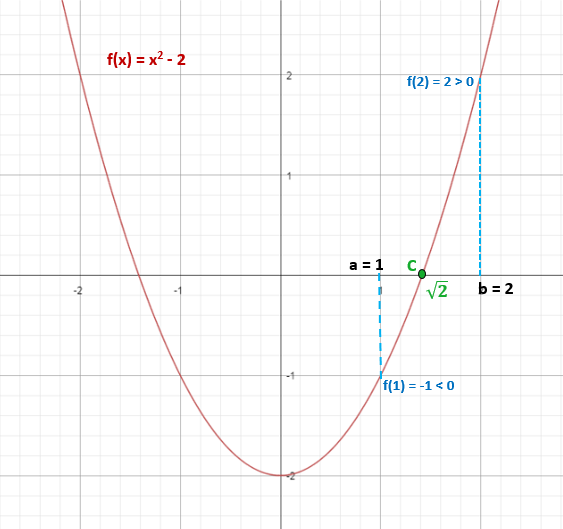
Tentukan apakah fungsi f (x) = x² - 2, memiliki setidaknya satu solusi nyata dalam interval [1,2].

Larutan

Anda memiliki fungsi f (x) = x² - 2. Seperti halnya polinomial, itu berarti terus menerus dalam interval apa pun.

Itu diminta untuk menentukan apakah ia memiliki solusi nyata dalam interval [1, 2], jadi sekarang Anda hanya perlu mengganti ujung interval dalam fungsi untuk mengetahui tanda ini dan tahu apakah mereka memenuhi syarat menjadi berbeda:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (negatif)

f (2) = 2² - 2 = 2 (positif)

Oleh karena itu, tanda f (1) ≠ tanda f (2).

Ini memastikan bahwa setidaknya ada satu titik "C" yang termasuk dalam interval [1,2], di mana f (c) = 0.

Dalam hal ini, nilai "C" dapat dihitung dengan mudah sebagai berikut:

X² - 2 = 0

x = ± √2.

Dengan demikian, √2 ≈ 1.4 milik interval [1,2] dan memenuhi bahwa f (√2) = 0.

Latihan 2

Menunjukkan persamaan itu x⁵ + x + 1 = 0 memiliki setidaknya satu solusi nyata.

Larutan

Pertama kita perhatikan bahwa f (x) = x⁵ + X + 1 adalah fungsi polinomial, yang berarti terus menerus dalam semua bilangan real.

Dalam hal ini, tidak ada interval yang diberikan, jadi Anda harus memilih nilai secara intuitif, lebih disukai mendekati 0, untuk mengevaluasi fungsi dan menemukan perubahan tanda:

Jika interval [0, 1] digunakan, itu harus:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Karena tidak ada perubahan tanda, prosesnya diulangi dengan interval lain.

Jika interval [-1, 0] digunakan, Anda harus:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

Dalam interval ini ada perubahan tanda: tanda f (-1) ≠ tanda f (0), yang berarti bahwa fungsi f (x) = x⁵ + X + 1 memiliki setidaknya satu akar nyata "C" dalam interval [-1, 0], sedemikian rupa sehingga f (c) = 0. Dengan kata lain, memang benar x⁵ + x + 1 = 0 memiliki solusi nyata dalam interval [-1,0].