Teorema demonstrasi keberadaan dan keunikan, contoh dan latihan

Dia Teorema keberadaan dan keunikan menetapkan kondisi yang diperlukan dan memadai untuk persamaan diferensial urutan pertama, dengan kondisi awal yang diberikan, untuk memiliki solusi dan bahwa solusi ini juga merupakan satu -satunya. 

Namun, teorema tidak memberikan teknik atau indikasi bagaimana menemukan solusi semacam itu. Teorema keberadaan dan keunikan juga meluas ke persamaan diferensial dari urutan yang lebih tinggi dengan kondisi awal, yang dikenal sebagai masalah cauchy.

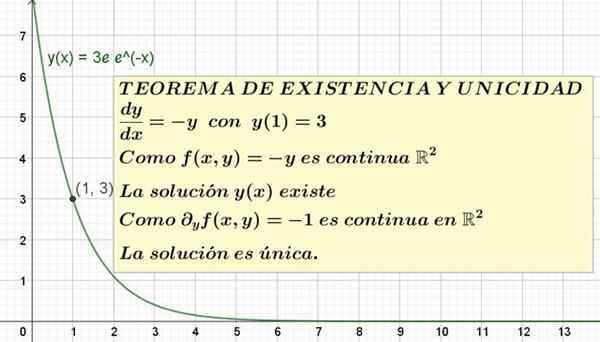
Gambar 1. Persamaan diferensial dengan kondisi awal dan solusinya ditampilkan. Teorema keberadaan dan keunikan menjamin bahwa itu adalah satu -satunya solusi yang mungkin.

Pernyataan formal dari teorema keberadaan dan keunikan adalah sebagai berikut:

"Untuk persamaan diferensial dan '(x) = f (x, y) dengan kondisi awal dan (a) = b,  ada setidaknya satu solusi di daerah persegi panjang pesawat Xy berisi intinya (A, b), Ya f (x, y) Itu terus menerus di wilayah itu. Dan jika turunan parsial F mengenai Dan: G = ∂f/ ∂y Ini terus menerus di daerah persegi panjang yang sama, sehingga solusinya unik dalam lingkungan titik tersebut (A, b) konten di wilayah kontinuitas F Dan G."

Kegunaan teorema ini pertama -tama terletak pada mengetahui apa daerah bidang XY di mana ada solusi dan juga tahu apakah solusi yang ditemukan adalah satu -satunya yang mungkin atau jika ada yang lain. 

Perhatikan bahwa jika kondisi unik.

[TOC]

Demonstrasi teorema keberadaan dan keunikan

Gambar 2. Kepada Charles émile Picard (1856-1941) Salah satu demonstrasi pertama dari teorema keberadaan dan keunikan terakreditasi. Sumber: Wikimedia Commons.

Untuk teorema ini, dua demonstrasi yang mungkin diketahui, salah satunya adalah demonstrasi Charles émile Picard (1856-1941) dan yang lainnya adalah karena Giuseppe Peano (1858-1932) berdasarkan karya Augustin Louis Cauchy (1789-1857 ).

Dapat melayani Anda: vektor bersamaan: karakteristik, contoh dan latihan

Perlu dicatat bahwa pikiran matematika paling terang pada abad ke -19 berpartisipasi dalam demonstrasi teorema ini, sehingga bisa menjadi intuit bahwa tak satu pun dari mereka yang sederhana.

Untuk secara formal menunjukkan teorema, perlu pertama -tama membuat serangkaian konsep matematika yang lebih maju, seperti fungsi tipe LipsChitz, ruang Banach, Karatheodory dan beberapa teorema keberadaan lagi, yang luput dari tujuan artikel tersebut.

Sebagian besar dari persamaan diferensial yang ditangani dalam fisika kesepakatan dengan fungsi berkelanjutan di wilayah yang diminati, oleh karena itu kita akan membatasi diri untuk menunjukkan cara di mana teorema diterapkan dalam persamaan sederhana.

Contoh

- Contoh 1

Pertimbangkan persamaan diferensial berikut dengan kondisi awal:

dan '(x) = - y; dengan dan (1) = 3

Apakah ada solusi untuk masalah ini? Apakah itu satu -satunya solusi yang mungkin?

Jawaban

Pertama, keberadaan solusi persamaan diferensial dievaluasi dan juga memenuhi kondisi awal. 

Dalam contoh ini f (x, y) = - y Kondisi keberadaan membutuhkan mengetahui jika  f (x, y) Itu terus menerus di wilayah pesawat Xy mengandung titik koordinat x = 1, y = 3.

Tetapi f (x, y) = -y Ini adalah fungsi terkait, yang terus menerus dalam domain bilangan real dan ada di seluruh rentang bilangan real.

Oleh karena itu disimpulkan bahwa f (x, y) kontinu dalam r², Jadi teorema menjamin keberadaan setidaknya satu solusi.

Mengetahui hal ini, sudah waktunya untuk menilai apakah solusinya unik atau jika sebaliknya ada lebih dari satu. Untuk ini perlu menghitung turunan parsial F Tentang variabel Dan:

∂f/∂y = ∂ (-y)/∂y = -1

Jadi G (x, y) = -1 yang merupakan fungsi konstan, yang juga didefinisikan untuk semua r² Dan itu juga terus menerus di sana. Oleh karena itu, teorema keberadaan dan keunikan menjamin bahwa masalah nilai awal ini memang memiliki solusi yang unik, meskipun tidak memberi tahu kami apa adanya.

Dapat melayani Anda: Cembung Poligon: Definisi, Elemen, Properti, Contoh

- Contoh 2

Pertimbangkan persamaan diferensial biasa -urutan pertama berikut dengan kondisi awal:

dan '(x) = 2√y; dan (0) = 0.

Apakah ada solusi dan (x) untuk masalah ini? Jika demikian, tentukan apakah ada satu atau lebih dari satu.

Menjawab

Kami mempertimbangkan fungsinya f (x, y) = 2√y. Fungsinya F hanya didefinisikan untuk y≥0, Nah, kita tahu bahwa jumlah negatif tidak memiliki akar nyata. Di samping itu f (x, y) Itu terus menerus di semiplane atas r²  termasuk sumbu x, jadi Penjamin Teorema Keberadaan dan Keunikan Setidaknya satu solusi di wilayah itu.

Sekarang, kondisi awal x = 0, y = 0 berada di tepi wilayah solusi. Kemudian kami mengambil turunan parsial F (x, y) sehubungan dengan y:

∂f/∂y = 1/√y

Dalam hal ini fungsi tidak didefinisikan untuk y = 0, tepatnya di mana kondisi awal berada.

Apa yang memberitahu kita teorema? Ini memberi tahu kita bahwa meskipun kita tahu bahwa setidaknya ada satu solusi semiplane atas sumbu x termasuk sumbu x, karena kondisi keunikan tidak terpenuhi, tidak ada jaminan bahwa ada satu solusi tunggal.

Ini berarti bahwa mungkin ada satu atau lebih dari satu solusi di wilayah kontinuitas f (x, y). Dan seperti biasa, teorema tidak memberi tahu kami apa yang bisa.

Latihan terpecahkan

- Latihan 1

Selesaikan masalah Cauchy dari Contoh 1:

dan '(x) = - y; dengan dan (1) = 3. 

Temukan fungsi y (x) yang memenuhi persamaan diferensial dan kondisi awal.

Larutan

Dalam Contoh 1 ditentukan bahwa masalah ini memiliki solusi dan juga unik. Untuk menemukan solusinya, hal pertama yang harus diperhatikan adalah bahwa itu adalah persamaan diferensial -legree pertama dari variabel yang dapat dipisahkan, yang ditulis sebagai berikut:

Dapat melayani Anda: koefisien variasi: untuk apa, perhitungan, contoh, latihan

dy /dx = - dan → dy = -y dx

Membagi antara dan di kedua anggota untuk memisahkan variabel yang kami miliki:

dy/y = - dx

Integral yang tidak terbatas pada kedua anggota diterapkan:

∫ (1/y) dy = - ∫dx

Memecahkan integral yang tidak terbatas adalah:

ln (y) = -x + c

di mana C adalah konstanta integrasi yang ditentukan oleh kondisi awal:

ln (3) = -1 + C, artinya C = 1 + ln (3)

Mengganti nilai C dan reorganisasi adalah:

ln (y) - ln (3) = -x + 1

Menerapkan properti logaritma berikut:

Perbedaan logaritma adalah logaritma hasil bagi

Ekspresi sebelumnya dapat ditulis ulang seperti ini:

ln (y/3) = 1 - x

Fungsi eksponensial diterapkan dengan kedua anggota untuk mendapatkan:

Y / 3 = e^{(1 - x)}

Yang setara dengan:

 y = 3e e^-X

Ini adalah solusi unik dari persamaan dan '= -y dengan y (1) = 3. Grafik solusi ini ditunjukkan pada Gambar 1.

- Latihan 2

Temukan dua solusi untuk masalah yang diangkat dalam Contoh 2:

dan '(x) = 2√ (y); dan (0) = 0.

Larutan

Ini juga merupakan persamaan dari variabel terpisah, yang ditulis secara berbeda tetap:

Dy / √ (y) = 2 dx

Mengambil integral yang tidak terbatas pada kedua anggota tetap:

2 √ (y) = 2 x + c

Seperti diketahui itu y≥0 Di wilayah solusi kami memiliki:

y = (x + c)² 

Tetapi karena kondisi awal x = 0, y = 0 harus dipenuhi, maka konstanta C adalah nol dan solusi berikut tetap:

dan (x) = x².

Tetapi solusi ini tidak unik, fungsi y (x) = 0 juga merupakan solusi dari masalah yang diangkat. Teorema keberadaan dan keunikan yang diterapkan pada masalah ini dalam Contoh 2 telah meramalkan bahwa mungkin ada lebih dari satu solusi.

Referensi

1. Coddington, Earl A.; Levinson, Norman (1955), Teori Persamaan Diferensial Biasa, New York: McGraw-Hill.
2. Encyclopedia of Mathematics. Teorema Cauchy-Lipschitz. Pulih dari: ensiklopediaofmath.org
3. Lindelöf, L'A South Application dari Methode des a Approksimations Berhasil aux équation Différentielles Ordinaires du Premier Ordre; Compttes rendus hebdomadaires des séances de l'm acadequie des sciences. Vol. 116, 1894, pp. 454-457. Pulih dari: gallic.BNF.fr.
4. Wikipedia. Metode pendekatan berturut -turut Picard. Pulih dari: is.Wikipedia.com
5. Wikipedia. Teorema Picard-Lindelöf. Pulih dari: is.Wikipedia.com.
6. Zill, d.1986. Persamaan diferensial dasar dengan aplikasi.Prentice Hall.