Teorema Lamy
- 2302
- 475
- Miss Marion Graham

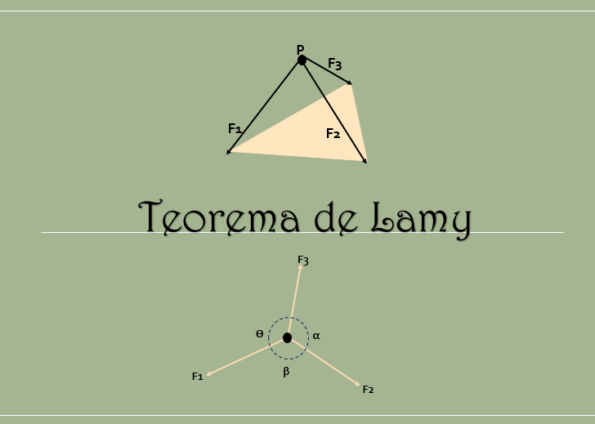
Teorema Lamy menetapkan bahwa ketika tubuh yang kaku seimbang dan pada aksi tiga kekuatan bait (kekuatan yang berada di bidang yang sama), garis aksi mereka setuju pada titik yang sama.
Teorema ini disimpulkan oleh ahli fisika dan agama Prancis. Itu banyak digunakan untuk menemukan nilai sudut, garis aksi suatu gaya atau untuk membentuk segitiga gaya.
Penjelasan
Teorema menetapkan bahwa agar kondisi keseimbangan dipenuhi, kekuatan harus coplanares; yaitu, jumlah gaya yang diberikan pada titik adalah nol.
Selain itu, seperti yang terlihat pada gambar berikut, dipenuhi bahwa dengan memperpanjang garis aksi ketiga kekuatan ini, mereka setuju pada titik yang sama.
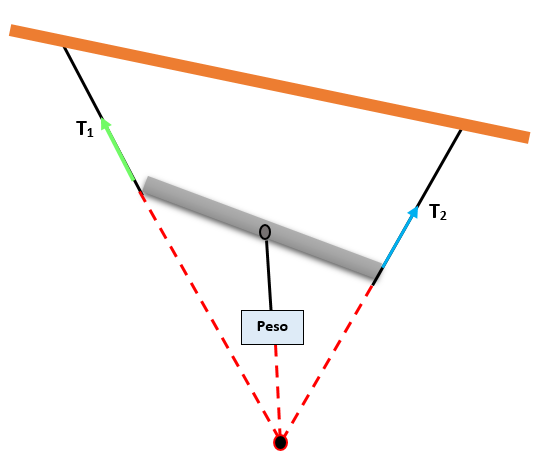
Dengan demikian, jika tiga gaya yang berada di bidang yang sama dan bersamaan, besarnya masing -masing gaya akan sebanding dengan dada dari sudut yang berlawanan, yang dibentuk oleh dua gaya lainnya.
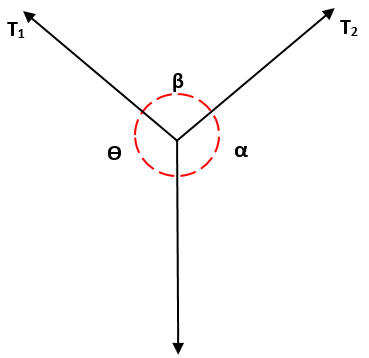
Ini harus T1, mulai dari payudara α, sama dengan rasio T2 / β, yang pada gilirannya sama dengan rasio T3 / ɵ, yaitu:
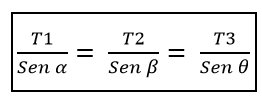
Dari sana ia mengikuti bahwa modul dari ketiga kekuatan ini harus sama jika sudut yang membentuk setiap pasangan gaya sama dengan 120º.
Ada kemungkinan bahwa salah satu sudutnya tumpul (ukur antara 900 dan 1800). Dalam hal ini payudara sudut itu akan sama dengan dada sudut tambahan (pada pasangannya mengukur 1800).
Dapat melayani Anda: hukum eksponenOlahraga diselesaikan
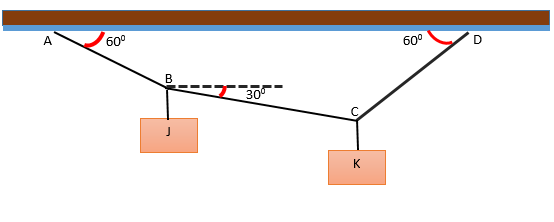
Ada sistem yang dibentuk oleh dua blok J dan K, yang menggantung pada beberapa string yang membentuk sudut sehubungan dengan horizontal, seperti yang ditunjukkan pada gambar. Sistem ini berada dalam keseimbangan dan blok j beratnya 240 n. Tentukan berat blok k.
Larutan
Dengan prinsip tindakan dan reaksi, ketegangan yang diberikan dalam blok 1 dan 2 akan sama dengan beratnya.
Sekarang diagram tubuh bebas dibangun untuk setiap blok dan dengan demikian menentukan sudut yang membentuk sistem.
Diketahui bahwa tali yang pergi ke A ke B, memiliki sudut 300 , sehingga sudut yang melengkapi sama dengan 600 . Dengan begitu Anda mencapai 900.
Di sisi lain, di mana titik A berada, ada sudut 600 sehubungan dengan horizontal; Sudut antara vertikal dan tKE Itu akan menjadi = 1800 - 600 - 900 = 300.
Dengan demikian diperoleh bahwa sudut antara AB dan BC = (300 + 900 + 300) dan (600 + 900 + 60) = 1500 dan 2100. Saat bergabung diverifikasi bahwa sudut total adalah 3600.
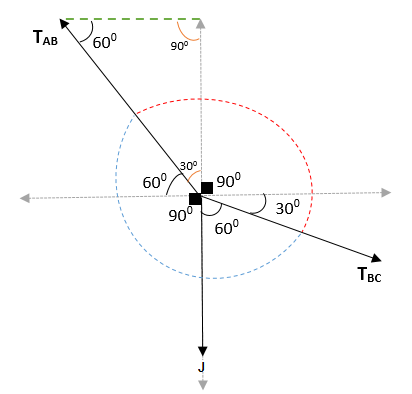
Menerapkan Teorema Lamy Anda harus:
TBc/ sin 1500 = PKE/ sin 1500
TBc = PKE
TBc = 240n.
Pada titik C, di mana blok, sudut antara horizontal dan tali BC adalah 30 adalah 30 adalah 300, Jadi sudut komplementer sama dengan 600.
Di sisi lain, ada sudut 600 di titik CD; Sudut antara vertikal dan tC Itu akan menjadi = 1800 - 900 - 600 = 300.
Dapat melayani Anda: Coplanares Points: Persamaan, Contoh, dan Latihan TerpecahkanDengan demikian diperoleh bahwa sudut di blok k adalah = (300 + 600)
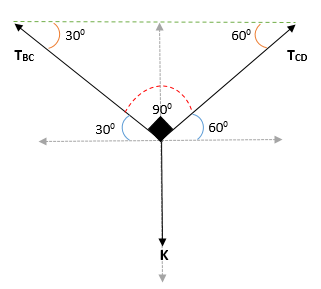
Menerapkan teorema Lamy di titik C:
TBc/ sin 1500 = B / sin 900
Q = tBc * Sen 900 / sin 1500
Q = 240 N * 1/0,5
Q = 480 n.
Referensi
- Ferdinand p. Bir, e. R. (2013). Mekanika untuk Insinyur, Statis. McGraw-Hill Inter-American.
- Francisco Español, J. C. (2015). Masalah aljabar linier terpecahkan. Edisi paraninfo, s.KE.
- Graham, j. (2005). Kekuatan dan gerakan. Houchton Mifflin Harcourt.
- Harpe, hlm. D. (2000). Topik dalam teori kelompok geometris. University of Chicago Press.
- P. Tpler y, g. M. (2005). Fisika untuk Sains dan Teknologi. Volume I. Barcelona: Kembalikan Anda.KE.

