Deskripsi Teorema Norton, Aplikasi, Contoh dan Latihan

Dia Teorema Norton, yang berlaku untuk sirkuit listrik, menetapkan bahwa sirkuit linier dengan dua terminal A dan B, dapat diganti dengan yang sama sekali setara, terdiri dari sumber saat ini yang disebut i_TIDAK terhubung secara paralel dengan resistensi r_TIDAK.

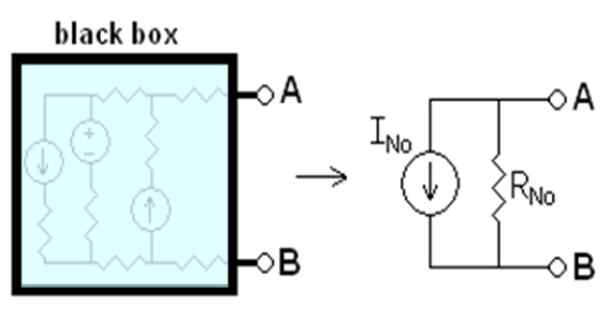
Kata saat ini saya_TIDAK saya dengar_N Itu adalah salah satu yang akan mengalir di antara titik -titik A dan B, jika mereka sirkit pendek. Perlawanan r_N Ini adalah resistensi yang setara antara terminal, ketika semua sumber independen dinonaktifkan. Segala sesuatu yang dikatakan skema pada Gambar 1.

Gambar 1. Sirkuit setara Norton. Sumber: Wikimedia Commons. Drumkid [CC BY-SA 3.0 (http: // createveCommons.Org/lisensi/by-sa/3.0/]]

Kotak hitam pada gambar berisi sirkuit linier yang akan diganti dengan yang setara dengan Norton. Sirkuit linier adalah yang ada di mana input dan output memiliki ketergantungan linier, seperti hubungan antara tegangan V dan arus langsung I dalam elemen ohmik: v = i.R.

Ekspresi ini sesuai dengan hukum Ohm, di mana R adalah resistensi, yang juga bisa menjadi impedansi, jika itu adalah sirkuit arus yang bergantian.

Teorema Norton dikembangkan oleh Electricist dan Penemu Edward L Engineer. Norton (1898-1983), yang bekerja untuk waktu yang lama untuk laboratorium Bell.

[TOC]

Aplikasi Norton Theorem

Ketika mereka memiliki jaringan yang sangat rumit, dengan banyak resistensi atau impedansi dan Anda menginginkan sirkuit yang lebih kecil dan lebih mudah dikelola.

Dengan cara ini, teorema Norton sangat penting ketika merancang sirkuit dengan banyak elemen, serta mempelajari respons mereka.

Hubungan antara Teorema Norton dan Thevenin

Teorema Norton adalah teorema ganda thevenin, yang berarti mereka setara. Teorema Thevenin menunjukkan bahwa kotak hitam pada Gambar 1 dapat diganti dengan sumber tegangan seri dengan resistensi, yang disebut resistensi revenin r_Th. Ini diekspresikan dalam gambar berikut:

Dapat melayani Anda: Mekanika Material: Sejarah, bidang studi, aplikasi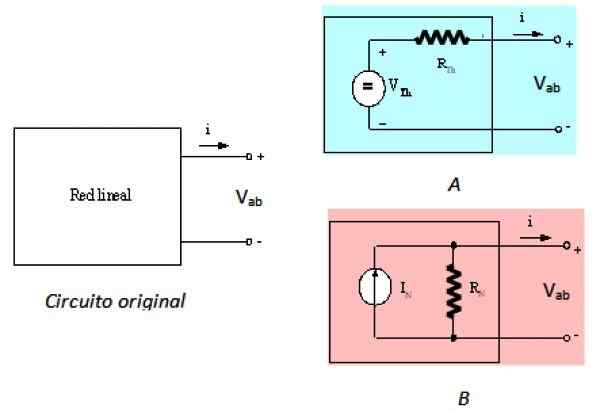 Gambar 2. Sirkuit Kiri Asli, dan padanannya dari Thévenin dan Norton. Sumber: f. Zapata.

Sirkuit kiri adalah sirkuit asli, jaringan linier dalam kotak hitam, sirkuit ke kanan adalah setara dengan thevenin dan sirkuit B Itu setara dengan Norton, seperti yang dijelaskan. Terlihat dari terminal A dan B, tiga sirkuit setara.

Sekarang amati itu:

-Di sirkuit asli ketegangan antara terminal adalah V_AB.

-V_AB  = V_Th di sirkuit KE

-Akhirnya, v_AB  = I_N.R_N di sirkuit B

Jika terminal A dan B adalah sirkuit pendek di tiga sirkuit, harus dipenuhi bahwa tegangan dan arus antara titik -titik ini harus sama untuk ketiganya, karena mereka setara. Jadi:

-Di sirkuit asli arusnya adalah i.

-Untuk sirkuit A, arusnya adalah i = v_Th / R_Th, Menurut hukum Ohm.

-Akhirnya di sirkuit B, arusnya adalah saya_N

Oleh karena itu disimpulkan bahwa resistensi Norton dan Thevenin memiliki nilai yang sama, dan bahwa arus diberikan oleh:

i = i_N = V_Th / R_Th = V_Th / R_N

Contoh

Untuk menerapkan teorema Norton dengan benar, langkah -langkah berikut diikuti:

-Bagian Sirkuit yang akan ditemukan oleh Norton Equivalent dari jaringan dari jaringan dari jaringan.

-Di sirkuit yang tersisa, tunjukkan terminal A dan B.

-Ganti sumber tegangan dengan sirkuit pendek dan arus dengan sirkuit terbuka, untuk menemukan resistansi yang setara antara terminal A dan B. Ini r_N.

-Kembalikan semua sumber ke posisi semula, sirkuit pendek terminal A dan B dan temukan arus yang beredar di antara mereka. Ini saya_N.

Dapat melayani Anda: efek doppler: deskripsi, rumus, kasus, contoh

-Gambar sirkuit ekivalen norton sesuai dengan apa yang ditunjukkan pada Gambar 1. Keduanya, sumber saat ini dan resistensi yang setara secara paralel.

Anda juga dapat menerapkan teorema Thevenin untuk menemukan R_Th, yang sudah kita ketahui sama dengan r_N, Kemudian oleh hukum Ohm, Anda dapat menemukan saya_N Dan sirkuit yang dihasilkan ditarik.

Dan sekarang mari kita lihat contoh:

Temukan setara Norton antara titik A dan B dari sirkuit berikut:

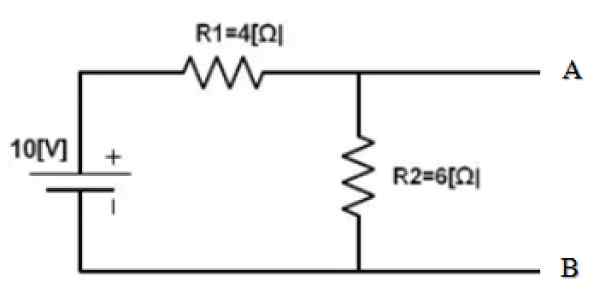Gambar 3. Sirkuit contoh. Sumber: f. Zapata.

Bagian dari sirkuit sudah terisolasi yang setara harus ditemukan. Dan poin A dan B ditentukan dengan jelas. Berikut ini adalah dengan sirkuit pendek sumber 10 V dan menemukan resistansi yang setara dari sirkuit yang diperoleh:

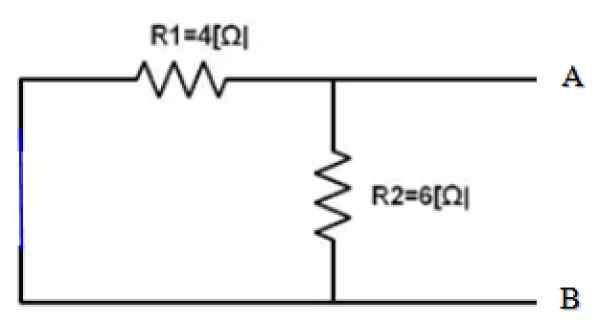Gambar 4. Sumber Sirkuit Pendek. Sumber: f. Zapata.

Tampilan dari terminal A dan B, keduanya resistensi R₁ dan r₂ Mereka secara paralel, oleh karena itu:

1/r_Persamaan = 1/r₁₂ = (1/4) + (1/6) Ω^-1 = 5/12 Ω^-1  → R_Persamaan = 12/5 Ω = 2.4 Ω

Kemudian sumber dikembalikan ke tempatnya dan titik -titik A dan B adalah sirkuit pendek untuk menemukan arus yang beredar di sana, ini akan terjadi_N. Dalam hal itu:

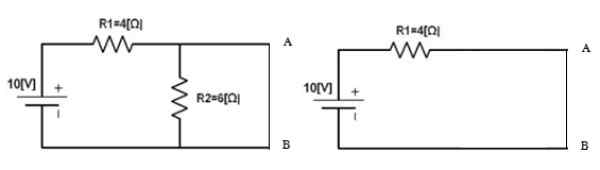Gambar 5. Sirkuit untuk menghitung arus norton. Sumber: f. Zapata.

yo_N = 10 V / 4 Ω = 2.5 a

Setara norton

Akhirnya, setara Norton dengan nilai -nilai yang ditemukan ditarik:

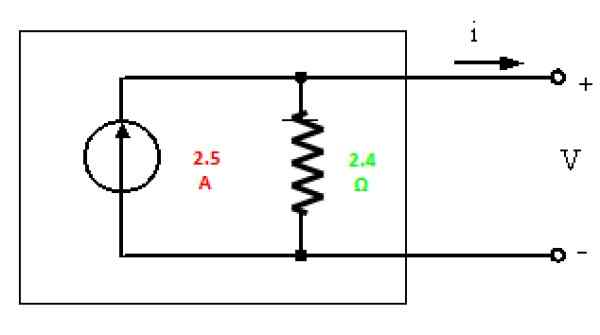Gambar 6. Norton setara dengan sirkuit pada Gambar 3. Sumber: f. Zapata.

Olahraga diselesaikan

Di sirkuit gambar berikut:

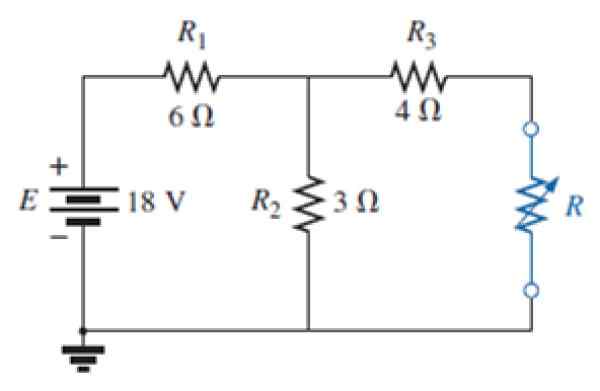Gambar 7. Sirkuit untuk latihan diselesaikan. Sumber: Alexander, C. 2006. Yayasan Sirkuit Listrik. 3. Edisi. MC Graw Hill.

a) Temukan sirkuit setara Norton dari jaringan resistensi biru luar.

b) juga menemukan setara dengan Thévenin.

Solusi untuk

Mengikuti langkah -langkah yang ditunjukkan di atas, sumber harus pendek -sirkuit:

Dapat melayani Anda: difraksi suara: apa yang terdiri dari contoh, aplikasi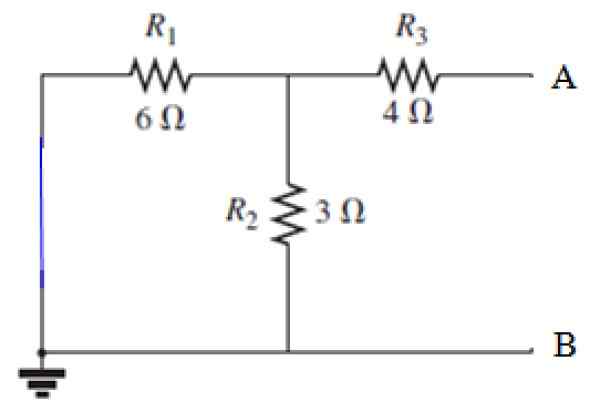 Angka 8. Sumber sirkuit pendek di sirkuit pada Gambar 7. Sumber: f. Zapata.

Perhitungan RN

Lihat dari terminal A dan B, resistensi R₃ adalah seri dengan paralel yang dibentuk oleh resistensi r₁ dan r₂, Mari kita hitung resistansi yang setara dari paralel ini:

1/r₁₂ = (1/6)+ (1/3) Ω^-1 = 1/2 Ω^-1  → R_Persamaan = 2/1 Ω = 2Ω

Dan kemudian paralel ini dalam seri dengan R_3, sehingga resistensi yang setara adalah:

R_Persamaan = 2 Ω + 4 Ω = 6 Ω

Ini adalah nilai dari kedua r_N pada r_Th, seperti yang dijelaskan sebelumnya.

Perhitungan IN

Kemudian terminal A dan B adalah sirkuit pendek, mengembalikan sumbernya ke tempatnya:

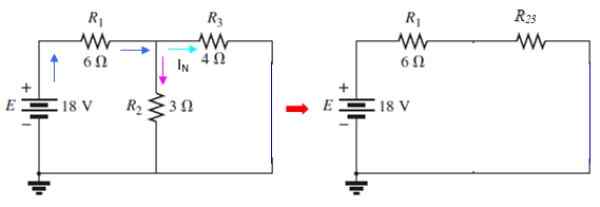Gambar 9. Sirkuit Arus Norton. Sumber: f. Zapata.

Saat ini melewati i₃ adalah saat ini i_N dicari, yang dapat ditentukan dengan metode mesh atau menggunakan seri dan paralel. Di sirkuit ini₂ dan r₃ Mereka paralel:

1/r₂₃ = (1/3)+ (1/4) Ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Perlawanan r₁ Seri dengan paralel ini, lalu:

R₁₂₃ = 6 + (12/7) Ω = 54/7 Ω

Arus yang keluar dari sumber (warna biru) dihitung oleh hukum Ohm:

V = i. R → I = V/R = 18 V/(54/7 Ω) = 7/3 a

Arus ini dibagi menjadi dua bagian: satu yang melintasi R₂ Dan satu lagi yang melintasi R₃. Namun, arus yang melintasi paralel R₂₃ Itu sama yang melewati r₁, seperti yang dapat dilihat di sirkuit perantara dari gambar tersebut. Tegangan di sana adalah:

V₂₃ = I.R₂₃ = (7/3) a .(12/7) Ω = 4 V

Kedua resistensi r₂ dan r₃ Mereka berada pada tegangan itu, karena mereka secara paralel, karenanya:

yo₃ = V₂₃ / R₃ = 4 V / 4 Ω = 1 a

Kami sudah memiliki Norton Current yang dicari, karena seperti yang dikatakan sebelumnya saya₃ = I_N, Jadi:

yo_N = 1 a

Setara norton

Semuanya siap untuk menggambar norton yang setara dengan sirkuit ini antara titik A dan B:

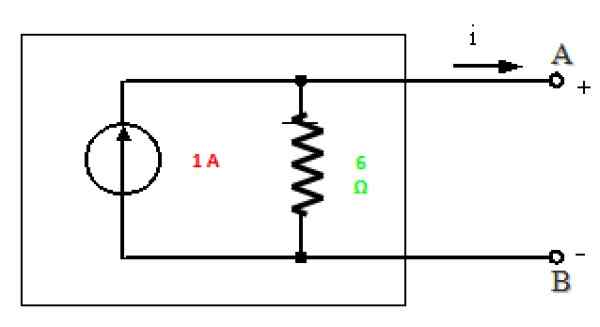Gambar 10. Norton setara dengan sirkuit pada Gambar 7. Sumber: f. Zapata.

Solusi b

Menemukan padanan Thévenin sangat sederhana, karena r_Th = R_N= 6 Ω dan seperti yang dijelaskan di bagian sebelumnya:

V_Th = I_N. R_N = 1 a . 6 Ω = 6 V

Sirkuit setara Thévenin adalah:

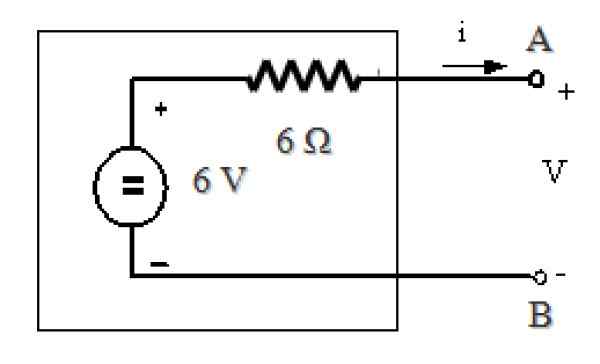Gambar 11. Setara dengan sirkuit Thevenin pada Gambar 7. Sumber: f. Zapata.

Referensi

1. Alexander, c. 2006. Yayasan Sirkuit Listrik. 3. Edisi. MC Graw Hill.
2. Boylestad, r. 2011. Pengantar Analisis Sirkuit. 2nd. Edisi. Pearson.
3. Dorf, r. 2006. Pengantar Sirkudan Listrik. 7. Edisi. John Wiley & Sons.
4. Edminister, J. seribu sembilan ratus sembilan puluh enam. Rangkaian listrik. Seri Schaum. 3. Edisi. MC Graw Hill.
5. Wikipedia. Teorema Norton . Pulih dari: itu.Wikipedia.org.