Penjelasan teori overlay, aplikasi, latihan diselesaikan

Dia Teorema Superposisi, Dalam sirkuit listrik, ia menetapkan bahwa tegangan antara dua titik, atau arus melalui mereka, adalah jumlah aljabar dari tegangan (atau arus jika itu masalahnya), karena masing -masing sumber, seolah -olah masing -masing bertindak dalam a cara independen.

Teorema ini memungkinkan menganalisis sirkuit linier yang mengandung lebih dari satu sumber independen, karena hanya perlu untuk menghitung kontribusi masing -masing secara terpisah.

Ketergantungan linier sangat menentukan bagi teorema. Sirkuit linier adalah bahwa responsnya berbanding lurus dengan entri.

Misalnya, hukum Ohm diterapkan pada resistensi listrik menetapkan itu V = i.R, Di mana V Itu adalah tegangan, R adalah perlawanan dan yo Ini adalah arus. Itu kemudian merupakan ketergantungan linier pada tegangan dan arus dalam resistensi.

Dalam sirkuit linier, prinsip superposisi diterapkan dengan mempertimbangkan hal berikut:

-Setiap sumber tegangan independen harus dipertimbangkan secara terpisah dan untuk ini perlu mematikan semua yang lain. Itu cukup untuk dimasukkan ke 0 V semua yang tidak dianalisis atau menggantinya dalam skema dengan sirkuit pendek.

-Jika sumbernya maka sirkuit harus dibuka.

-Ketika resistansi internal sumber arus dan tegangan dipertimbangkan, ini harus tetap di tempatnya, menjadi bagian dari sisa sirkuit.

-Jika ada sumber dependen, mereka harus seperti yang muncul di sirkuit.

[TOC]

Aplikasi

Teorema yang tumpang tindih digunakan untuk mendapatkan sirkuit yang lebih sederhana dan lebih mudah untuk ditangani. Tetapi harus diingat bahwa hanya berlaku untuk mereka yang memiliki respons linier, seperti yang dinyatakan di awal.

Maka tidak dapat digunakan secara langsung untuk menghitung daya misalnya, karena daya terkait dengan arus hingga:

P = i² R

Karena arus kuadrat, jawabannya tidak linier. Juga tidak berlaku untuk sirkuit magnetik di mana transformer campur tangan.

Dapat melayani Anda: listrik dinamis

Di sisi lain, teorema superposisi memberikan kesempatan untuk mengetahui efek yang dimiliki setiap sumber pada sirkuit. Dan tentu saja, melalui aplikasinya adalah mungkin untuk menyelesaikannya sepenuhnya, yaitu, untuk mengetahui arus dan voltase melalui setiap resistensi.

Teorema yang tumpang tindih juga dapat digunakan bersama dengan teorema sirkuit lain, misalnya bahwa dari Thévenin, untuk memecahkan konfigurasi yang lebih kompleks.

Dalam sirkuit arus bolak -balik, teorema juga berguna. Dalam hal ini, kami bekerja dengan impedansi alih -alih resistensi, selama respons total dari setiap frekuensi independen dapat dihitung.

Akhirnya, dalam sistem elektronik teorema ini berlaku untuk analisis arus langsung dan alternatif, secara terpisah.

Langkah -langkah untuk menerapkan teorema tumpang tindih

-Nonaktifkan semua sumber independen yang mengikuti instruksi yang diberikan di awal, kecuali yang akan dianalisis.

-Tentukan output, baik tegangan atau arus, yang menghasilkan sumber tunggal itu.

-Ulangi dua langkah yang dijelaskan untuk semua sumber lainnya.

-Hitung jumlah aljabar dari semua kontribusi yang ditemukan dalam langkah -langkah sebelumnya.

Latihan terpecahkan

Contoh -contoh diselesaikan di bawah ini mengklarifikasi penggunaan teorema di beberapa sirkuit sederhana.

- Contoh 1

Di sirkuit yang ditunjukkan pada gambar berikut, temukan arus yang melintasi setiap resistansi melalui teorema yang tumpang tindih.

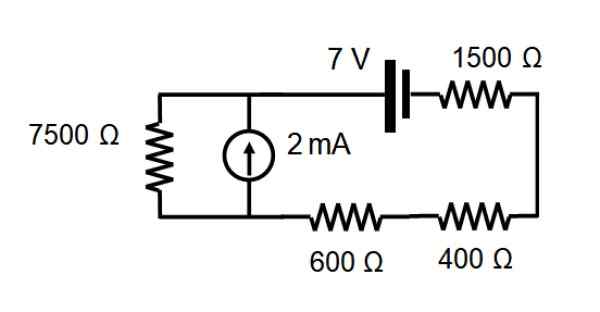
Larutan

Kontribusi Sumber Tegangan

Untuk memulai sumber saat ini dieliminasi, dengan mana sirkuit tetap seperti ini:

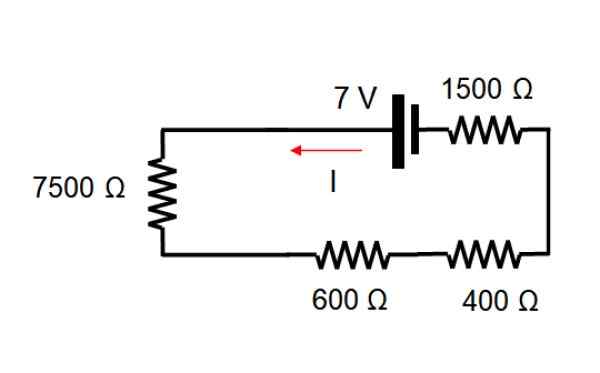
Resistansi yang setara adalah menambahkan nilai masing -masing resistensi, karena semuanya dalam seri:

7500 +600 +400 +1500 Ω = 10.000 Ω

Menerapkan Hukum Ohm V = i.R Dan membersihkan arus:

I = v / r = 7/10.000 a = 0.0007 a = 0.7 ma

Arus ini sama untuk semua perlawanan.

Dapat melayani Anda: Millikan Eksperimen: Prosedur, Penjelasan, Pentingnya

Kontribusi sumber saat ini

Sumber tegangan segera dihilangkan, hanya bekerja dengan sumber saat ini. Sirkuit yang dihasilkan ditunjukkan di bawah ini:

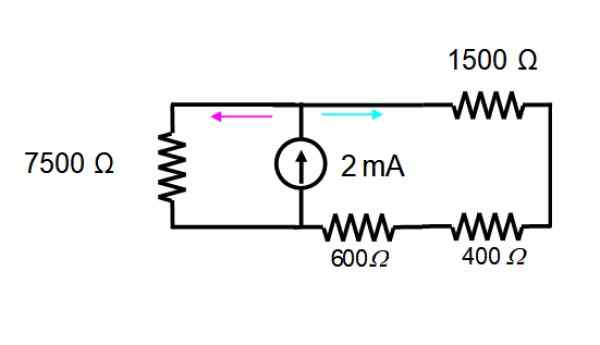
Resistensi dalam jala di sebelah kanan berada dalam seri dan dapat diganti dengan hanya satu:

600 +400 + 1500 Ω = 2500 Ω

Sirkuit yang dihasilkan seperti ini:

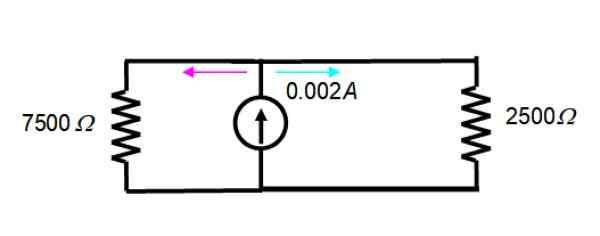
Arus 2 mA = 0.002 A dibagi antara dua resistensi gambar, oleh karena itu persamaan pembagi saat ini valid:

yo_X = (R_Persamaan/R_X)YO_T

Di mana yo_X adalah arus dalam resistensi R_X, R_Persamaan melambangkan resistensi yang setara dan yo_T adalah arus total. Penting untuk menemukan resistensi yang setara di antara mereka, mengetahui bahwa:

1/r_Persamaan = (1/ r₁) + (1/ r₂)

Karena itu:

1/r_Persamaan = (1/7500) + (1/2500) = 1/1875 → R_Persamaan = 1875 Ω

Untuk sirkuit lain ini, arus yang melewati resistansi 7500 Ω mengganti nilai dalam persamaan pembagian arus:

yo_{7500 Ω} = (1875/7500). 0.002 a = 0.0005 a = 0.5 ma

Sedangkan yang melewati resistensi 2500 Ω adalah:

yo_{2500 Ω} = 2 ma - 0.5 mA = 1.5 ma

Aplikasi Teorema Superposisi

Sekarang teorema yang tumpang tindih untuk setiap resistansi diterapkan, dimulai dengan 400 Ω:

yo_{400 Ω} = 1.5 ma - 0.7 mA = 0.8 ma

Penting: Untuk resistensi ini, arus dikurangi, karena mereka beredar ke arah yang berlawanan, seperti yang dapat dilihat dari pengamatan yang cermat dari gambar, di mana indera arus memiliki warna yang berbeda.

Arus yang sama ini sama dengan resistansi 1500 Ω dan 600 Ω, karena semuanya dalam seri.

Kemudian teorema diterapkan untuk menemukan arus melalui resistansi 7500 Ω:

yo_{7500 Ω} = 0.7 ma + 0.5 mA = 1.2 ma

Penting: Dalam kasus resistansi 7500 Ω, amati bahwa arus ditambahkan, karena di kedua sirkuit mereka bersirkulasi ke arah yang sama ketika melewati resistensi ini. Sekali lagi perlu untuk mengamati dengan hati -hati indera arus.

Dapat melayani Anda: Kesalahan relatif: rumus, bagaimana itu dihitung, latihan

- Latihan 2

Temukan arus dan tegangan melalui resistansi 12 Ω melalui teorema yang tumpang tindih.

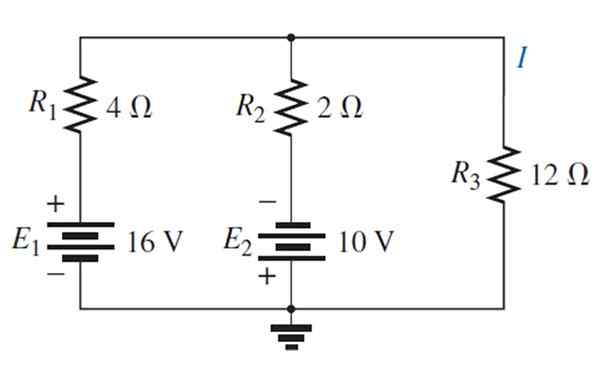
Larutan

Sumber E diganti₁ Dengan sirkuit pendek:

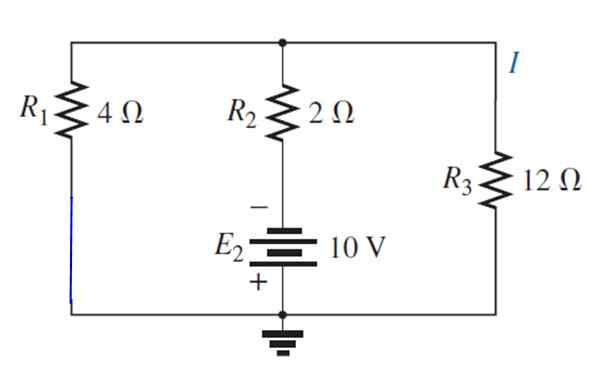
Sirkuit yang dihasilkan ditarik sebagai berikut, untuk dengan mudah memvisualisasikan resistor yang tetap paralel:

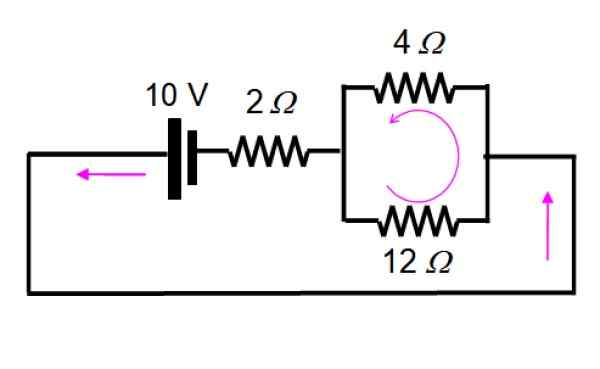
Dan sekarang diselesaikan dengan menerapkan seri dan paralel:

1/r_Persamaan = (1/12) + (1/4) = 1/3 → r_Persamaan = 3 Ω

Perlawanan ini pada gilirannya seri dengan itu 2 Ω, Oleh karena itu resistensi total 5 Ω. Total arus adalah:

I = v / r = 10 v / 5 Ω = 2 a

Arus ini dibagi sebagai:

yo_12Ω = (3/12) 2 a = 0.5 a

Oleh karena itu tegangannya adalah:

V_12Ω = 0.5 A × 12 Ω = 6 V

Sekarang sumbernya diaktifkan₁:

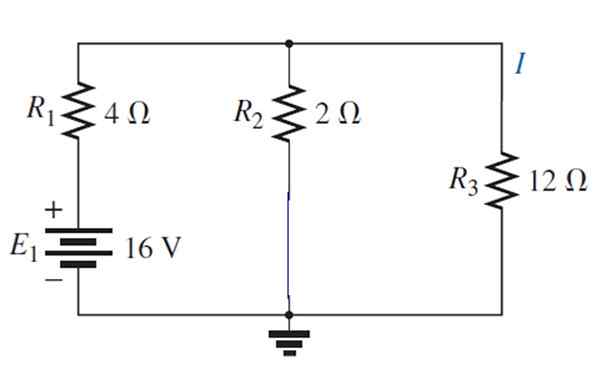
Sirkuit yang dihasilkan dapat ditarik dengan cara ini:

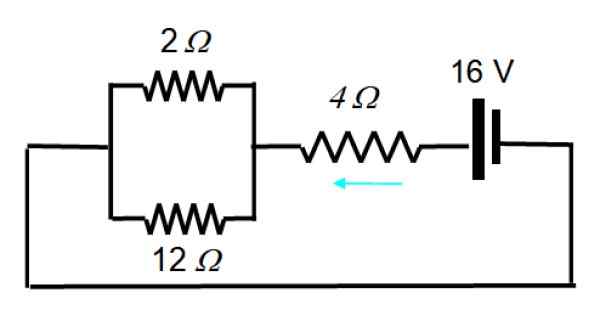
1/r_Persamaan = (1/12) + (1/2) = 7/12 → R_Persamaan = 12/7 Ω

Dan seri dengan 4 Ω Ini adalah resistensi yang setara 40/7 Ω. Dalam hal ini total arus adalah:

I = v/r = 16 V/(40/7) Ω = 14/5 a

Pembagi tegangan dengan nilai -nilai ini diterapkan lagi:

yo_12Ω = ((12/7)/12) (14/5) a = 0.4 a

Arus yang dihasilkan adalah: 0.lima puluh.4 A = 0.1 a. Perhatikan bahwa mereka telah dikurangi, karena arus setiap sumber membuat makna yang berbeda, seperti yang dapat dilihat di sirkuit asli.

Tegangan melalui resistensi adalah:

V_12Ω = 0.4 A × 12 Ω = 4.8 v

Akhirnya, tegangan total adalah: 6 V-4.8 V = 1.2 v

Referensi

1. Alexander, c. 2006. Yayasan Sirkuit Listrik. 3. Edisi. MC Graw Hill.
2. Boylestad, r. 2011. Pengantar Analisis Sirkuit. 2nd. Edisi. Pearson.
3. Dorf, r. 2006. Pengantar Sirkudan Listrik. 7. Edisi. John Wiley & Sons.
4. Edminister, J. seribu sembilan ratus sembilan puluh enam. Rangkaian listrik. Seri Schaum. 3. Edisi. MC Graw Hill
5. Wikipedia. Pembagi saat ini. Pulih dari: itu.Wikipedia.org.