Sifat matriks ortogonal, demonstrasi, contoh

Kamu memiliki satu Matriks ortogonal Ketika matriks tersebut dikalikan dengan transposnya menghasilkan matriks identitas. Jika kebalikan dari suatu matriks sama dengan yang ditransposkan maka matriks asli adalah ortogonal.

Matriks ortogonal adalah karakteristik bahwa jumlah baris sama dengan jumlah kolom. Selain itu, vektor baris adalah vektor unit ortogonal dan ruam vektor yang ditransposkan juga bersifat.

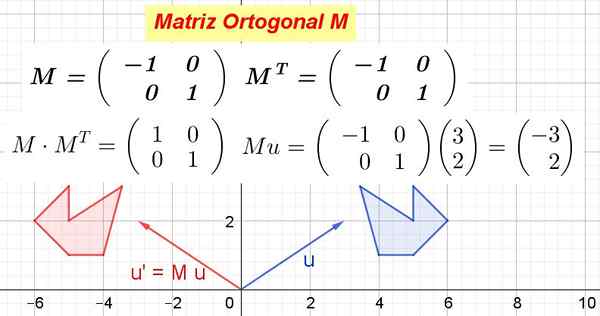Gambar 1. Contoh matriks ortogonal dan bagaimana mengubah objek geometris. (Disiapkan oleh Ricardo Pérez)

Ketika matriks ortogonal dikalikan dengan vektor ruang vektor menghasilkan a Transformasi isometrik, yaitu transformasi yang tidak mengubah jarak dan menjaga sudut.

Perwakilan khas matriks ortogonal adalah Matriks rotasi. Transformasi matriks ortogonal pada ruang vektor disebut Transformasi ortogonal.

Transformasi geometris rotasi dan refleksi titik yang diwakili oleh vektor -vektor kartesisnya dibuat dengan menerapkan matriks ortogonal pada vektor asli untuk mendapatkan koordinat vektor yang diubah. Karena alasan inilah matriks ortogonal banyak digunakan dalam pemrosesan grafik komputasi.

[TOC]

Properti

Array M Itu ortogonal jika dikalikan dengan transpose M^T matriks identitas menghasilkan yo. Demikian pula, produk transpos dari matriks ortogonal oleh matriks asli dari matriks identitas:

M m^T = M^T M = i

Sebagai konsekuensi dari pernyataan sebelumnya, transposa dari matriks ortogonal sama dengan matriks terbaliknya:

M^T = M^-1.

Set matriks dimensi ortogonal n x n Mereka membentuk kelompok ortogonal Atau (n). Dan bagian dari Atau (n) matriks ortogonal dengan menentukan +1 bentuk Kelompok Matriks Khususnya (N). Matriks kelompok Anda (n) Mereka adalah matriks yang menghasilkan transformasi rotasi linier, juga dikenal sebagai Grup rotasi.

Demonstrasi

Kami akan menunjukkan bahwa matriks adalah ortogonal jika, dan hanya jika, vektor baris (atau vektor kolom) ortogonal satu sama lain dan dari norma 1.

Dapat melayani Anda: Teorema Bayes

Asumsikan bahwa jajaran matriks ortogonal n x n adalah n n vektor ortonormal dimensi n. Jika dilambangkan dengan v1, v2,.. ., vN Vektor N terpenuhi:

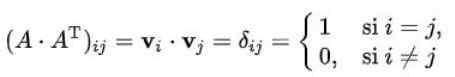
Di mana terbukti bahwa himpunan vektor baris adalah seperangkat vektor ortogonal dengan norma.

Contoh

Contoh 1

Tunjukkan bahwa matriks 2 x 2 yang dimiliki vektor di baris pertama V1= (-1 0) dan di baris kedua vektor V2= (0 1) adalah matriks ortogonal.

Larutan: Matriks dibangun M dan transpose dihitung M^T:

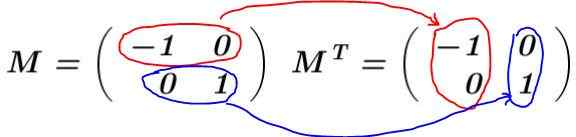
Dalam contoh ini, matriks M Ini adalah mobil yang ditransposkan, yaitu bahwa matriks dan transposnya identik. Itu berlipat ganda M untuk transpose M^T:

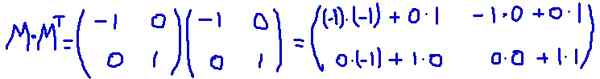
Itu diverifikasi itu M M^T Itu sama dengan matriks identitas:

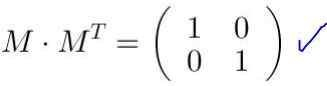
Saat matriks M Ini dikalikan dengan koordinat vektor atau titik, koordinat baru diperoleh yang sesuai dengan transformasi yang dibuat oleh matriks pada vektor atau titik.

Gambar 1 menunjukkan caranya M Mengubah vektor atau di dalam atau' Dan juga suka M Mengubah poligon biru menjadi poligon merah. Sebagai M Ini ortogonal, kemudian transformasi ortogonal, yang menjaga jarak dan sudut.

Contoh 2

Asumsikan bahwa Anda memiliki matriks 2 x 2 yang didefinisikan dalam reais yang diberikan oleh ekspresi berikut:

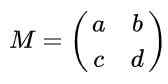
Temukan Nilai Nyata ke, B, C Dan D sehingga matriksnya M Jadilah matriks ortogonal.

Larutan: Menurut definisi, matriks adalah ortogonal jika dikalikan dengan transpose diperoleh sebagai hasilnya matriks identitas. Mengingat bahwa matriks yang ditransposkan diperoleh dari yang asli, pertukaran baris dengan kolom adalah kesetaraan berikut:

Itu dapat melayani Anda: domain dan kontradiksi suatu fungsi (dengan contoh)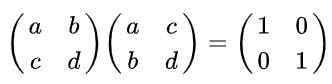

Melakukan multiplikasi matriks adalah:

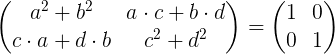
Menyamakan unsur -unsur matriks kiri dengan elemen matriks identitas di sebelah kanan, kami memperoleh sistem empat persamaan dengan empat yang tidak diketahui A, B, C dan D.

Kami mengusulkan untuk a, b, c dan d ekspresi berikut berdasarkan alasan trigonometri sinus dan cosinus:

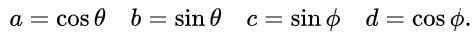
Dengan proposal ini dan karena identitas trigonometri mendasar, persamaan pertama dan ketiga dalam kesetaraan elemen matriks secara otomatis dipenuhi. Persamaan ketiga dan keempat adalah sama dan dalam kesetaraan matriks setelah mengganti nilai yang diusulkan adalah seperti ini:

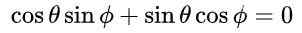
Yang mengarah ke solusi berikut:

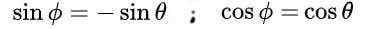
Akhirnya, solusi berikut diperoleh untuk matriks ortogonal M:

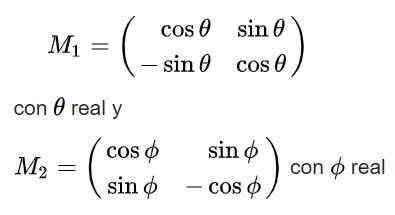
Perhatikan bahwa solusi pertama memiliki penentu +1 sehingga milik kelompoknya (2), sedangkan solusi kedua memiliki penentu -1 dan karenanya bukan milik kelompok ini.

Contoh 3

Mengingat matriks berikut, temukan nilai A dan B untuk memiliki matriks ortogonal.

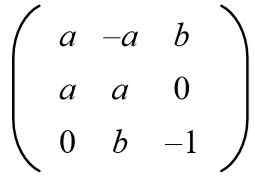
Larutan: Agar matriks tertentu menjadi ortogonal, produk dengan transpose harus menjadi matriks identitas. Kemudian, produk matriks dari matriks yang diberikan dengan matriks yang ditransposkan dibuat memberikan hasil berikut:

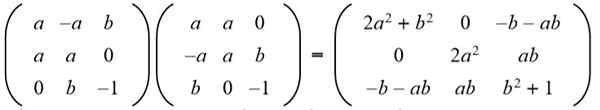
Selanjutnya, hasilnya cocok dengan matriks identitas 3 x 3:

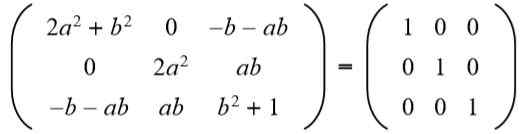
Di kolom ketiga baris kedua yang Anda miliki (A B = 0), Tetapi ke Itu tidak bisa nol, karena jika demikian, kesetaraan elemen baris kedua dan kolom kedua tidak akan terpenuhi. Lalu harus B = 0. Menggantikan B Untuk nilai 0 yang kita miliki:

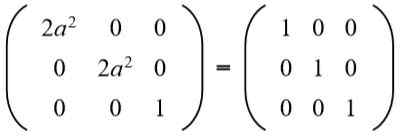
Kemudian persamaan diselesaikan: 2a^2 = 1, yang solusinya adalah: +½√2 dan -½√2.

Dapat melayani Anda: jenis sudut, karakteristik, dan contoh

Mengambil solusi positif untuk ke Ini menghasilkan matriks ortogonal berikut:

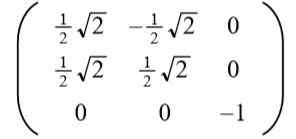
Pembaca dapat dengan mudah memverifikasi bahwa vektor baris (dan juga vektor kolom) adalah ortogonal dan unit, yaitu ortormal.

Contoh 4

Menunjukkan bahwa matriks KE siapa barisnya V1 = (0, -1 0), V2 = (1, 0, 0) Dan V3 = (0 0 -1) Itu adalah matriks ortogonal. Selain itu, temukan bagaimana vektor basis kanonik diubah I J K Ke vektor U1, U2 Dan U3.

Larutan: Harus diingat bahwa elemen (i, j) dari matriks dikalikan dengan transpose, adalah produk skalar dari vektor baris (i) oleh kolom (j) dari transpose. Selain itu, produk ini sama dengan Delta Kronecker jika matriksnya ortogonal:

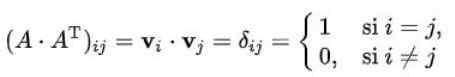
Dalam kasus kami, ini seperti ini:

V1 • V1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • V2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • V3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • V2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • V1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • V3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • V2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • V3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • V1 = 0x0 + 0x (-1) + (-1) x0 = 0

Dengan apa yang ditunjukkan bahwa itu adalah matriks ortogonal.

Di samping itu u1 = a = (0, 1, 0); U2 = a j = (-1, 0, 0) dan akhirnya U3 = a k = (0, 0, -1)

Referensi

1. Anthony Nicolaides (1994) Penentu & Matriks. Lulus publikasi.
2. Birkhoff dan Maclane. (1980). Aljabar Modern, Ed. Vicens-Vives, Madrid.
3. Casteleiro Villalba m.  (2004) Pengantar aljabar linier. Editorial ESIC.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Matematika: Panduan Kelangsungan Hidup Siswa. Cambridge University Press.
6. Richard J. Brown (2012) 30-detik Matematika: 50 teori yang paling banyak berkembang dalam matematika. Ivy Press Limited.
7. Wikipedia. Matriks ortogonal. Pulih dari: is.Wikipedia.com
8. Wikipedia. Matriks ortogonal. Diperoleh dari: di.Wikipedia.com