Teorema Thévenin Apa yang terdiri, aplikasi dan contoh
- 648
- 155
- Dewey Runolfsdottir
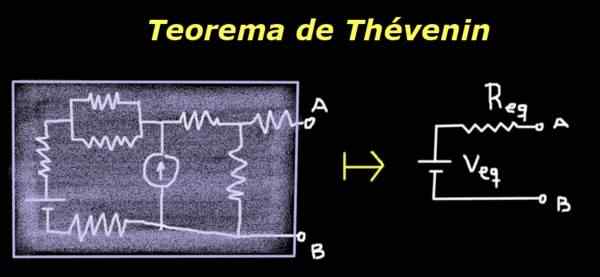
Dia Teorema Thévenin Ini menyatakan bahwa sirkuit dengan terminal A dan B dapat diganti dengan yang setara yang terdiri dari sumber dan resistansi seri, yang nilainya memberikan perbedaan potensial yang sama antara A dan B dan impedansi yang sama dengan sirkuit asli.
Teorema ini dirilis pada tahun 1883 oleh insinyur Prancis Léon Charles Thévenin, tetapi diklaim bahwa ia dinyatakan tiga puluh tahun sebelumnya oleh fisikawan Jerman Hermann von Helmholtz.
Gambar 1. Teorema Thévenin. Sumber: Made sendiri Kegunaannya terletak pada fakta bahwa, bahkan jika sirkuit asli kompleks atau tidak diketahui, untuk keperluan beban atau impedansi yang ditempatkan di antara terminal A dan B, sirkuit setara yang sederhana dari perilaku ini berperilaku dengan cara yang sama seperti aslinya yang asli dengan aslinya.
[TOC]
Bagaimana tegangan setara langkah demi langkah dihitung?
Tegangan atau perbedaan potensial dari sirkuit yang setara dapat diperoleh dengan cara berikut:
- Secara eksperimental
Memperoleh tegangan setara thévenin
Jika itu adalah perangkat atau peralatan yang ada dalam "kotak hitam", perbedaan potensial antara terminal A dan B dengan voltmeter atau osiloskop diukur. Sangat penting bahwa tidak ada beban atau impedansi antara terminal A dan B ditempatkan.
Voltmeter atau osiloskop tidak mewakili beban apa pun untuk terminal, karena kedua tim memiliki impedansi yang sangat besar (idealnya tak terbatas) dan seolah -olah terminal A dan B tanpa beban. Tegangan atau tegangan yang diperoleh dengan cara ini adalah ketegangan yang setara dari Thévenin.
Mendapatkan impedansi yang setara dari Thévenin
Untuk mendapatkan impedansi yang setara dari pengukuran eksperimental, resistansi yang diketahui antara terminal A dan B ditempatkan dan penurunan tegangan atau sinyal tegangan dengan osiloskop diukur.
Dari penurunan tegangan dalam resistansi yang diketahui di antara terminal, arus yang bersirkulasi melalui itu dapat diperoleh.
Produk arus yang diperoleh dengan resistansi setara ditambah penurunan tegangan yang diukur pada resistansi yang diketahui sama dengan tegangan setara dari temenin yang sebelumnya diperoleh. Dari kesetaraan ini, impedansi yang setara dari Thévenin dibersihkan.
- Memecahkan sirkuit
Perhitungan tegangan setara Thévenin
Pertama, beban atau impedansi terminal A dan B terputus.
Seperti yang diketahui sirkuit, Hukum Meshes atau Kirchhoff diterapkan untuk menemukan ketegangan di terminal. Ketegangan ini akan menjadi setara Thévenin.
Dapat melayani Anda: Gunung Olympus (Mars)Perhitungan impedansi yang setara Thévenin
Untuk mendapatkan impedansi yang setara, kami melanjutkan ke:
- Ganti sumber tegangan sirkuit asli dengan sirkuit pendek "impedansi nol" dan sumber sirkuit asli untuk "impedansi tak terbatas" terbuka.
- Kemudian impedansi yang setara dihitung mengikuti aturan impedansi seri dan impedansi secara paralel.
Aplikasi Teorema Thévenin (Bagian I)
Kami akan menerapkan teorema Thévenin untuk menyelesaikan beberapa sirkuit. Pada bagian pertama ini kami mempertimbangkan sirkuit yang hanya memiliki sumber dan resistensi tegangan.
Contoh 1 (Perhitungan tegangan setara langkah demi langkah)
Gambar 2 menunjukkan sirkuit yang ada dalam kotak surgawi yang masing -masing memiliki dua baterai gaya elektromotor V1 dan V2 dan resistensi R1 dan R2, sirkuit memiliki terminal A dan B yang dapat dihubungkan oleh beban yang dapat dihubungkan.
Gambar 2. Contoh 1 Teorema THévenin. Sumber: Made sendiri Tujuannya adalah untuk menemukan sirkuit setara thévenin, yaitu, menentukan nilai VT dan RT dari sirkuit yang setara. Terapkan nilai -nilai berikut: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω dan R = 1Ω.
Selangkah demi selangkah
Langkah 1
Kami akan menentukan tegangan di terminal A dan B ketika mereka tidak ditempatkan beban apapun.
Langkah 2
Sirkuit yang akan diselesaikan terdiri dari satu mesh yang melaluinya arus saya beredar yang telah kami ambil secara positif secara searah jarum jam.
Langkah 3
Kami bepergian dengan mesh dimulai dengan sudut kiri bawah. Rute mengarah ke persamaan berikut:
V1 - i*r1 - i*r2 - v2 = 0
Langkah 4
Kami menghapus arus mesh saya dan dapatkan:
I = (v1 -v2) / (r1 +r2) = (4v - 1v) / (3Ω +6Ω) = ⅓ a
Langkah 5
Dengan arus mesh kita dapat menentukan perbedaan tegangan atau tegangan antara A dan B, yaitu:
VAB = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Artinya tegangan setara Thevenin adalah: VT = 3V.
Langkah 6 (resistensi setara Thévenin)
Kami sekarang melanjutkan untuk menghitung resistensi setara Thévenin, yang dan seperti yang dikatakan sebelumnya, sumber tegangan digantikan oleh kabel.
Dalam hal ini, kami hanya memiliki dua perlawanan secara paralel, jadi resistensi setara Thévenin adalah:
Rt = (r1 * r2) / (r1 + r2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Contoh 1b (arus saat ini menggunakan setara Thévenin)
Hubungkan sebagai beban ke terminal A dan B A resistansi r = 1Ω ke sirkuit yang setara dan temukan arus yang bersirkulasi melalui beban tersebut.
Dapat melayani Anda: Gerakan Bujur Barat: Karakteristik, Jenis dan ContohLarutan
Ketika resistansi r terhubung ke sirkuit setara thevenin ada sirkuit sederhana yang terdiri dari sumber VT resistansi seri secara seri dengan resistansi r.
Kami akan menyebut arus yang beredar melalui beban r, sehingga persamaan mesh seperti ini:
VT - IC* RT - IC* R = 0
Dari mana ia diberikan IC yang diberikan oleh:
Ic = vt / (rt + r) = 3v / (2Ω + 1Ω) = 1 a
Verifikasi Teorema Thévenin
Untuk memverifikasi bahwa teorema Thévenin terpenuhi, hubungkan R ke sirkuit asli dan temukan arus yang beredar dengan R menerapkan hukum jerat ke sirkuit yang dihasilkan.
Sirkuit yang dihasilkan tetap dan persamaan meshnya seperti yang ditunjukkan pada gambar berikut:
Gambar 3. Arus mesh. (Elaborasi sendiri) Menambahkan persamaan mesh, dimungkinkan untuk menemukan I1 saat ini tergantung pada I2 saat ini. Kemudian diganti dalam persamaan mesh kedua dan ada persamaan dengan i2 sebagai satu -satunya yang tidak diketahui. Tabel berikut menunjukkan operasi.
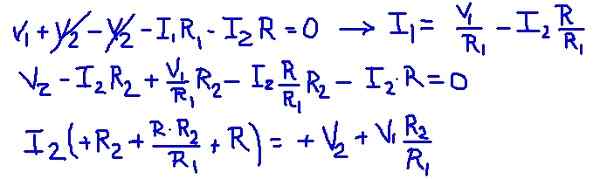Gambar 4. Detail Operasi. (Elaborasi sendiri) Kemudian nilai resistansi dan tegangan sumber diganti, mendapatkan nilai numerik dari arus mesh i2.
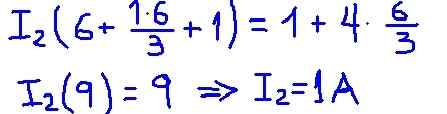Gambar 5. Detail Hasil. (Elaborasi sendiri) Aliran i2 mesh adalah arus yang beredar melalui resistansi beban R dan nilai yang ditemukan dari 1 A sepenuhnya bertepatan dengan apa yang sebelumnya ditemukan dengan sirkuit setara thévenin.
Penerapan Teorema Thévenin (Bagian II)
Pada bagian kedua ini, teorema Thévenin akan diterapkan di sirkuit yang memiliki sumber tegangan, sumber saat ini dan resistensi.
Contoh 2A (resistensi setara Thévenin)
Tujuannya adalah untuk menentukan sirkuit ekivalen dari thévenin yang sesuai dengan sirkuit dari gambar berikut, ketika terminal tanpa resistansi 1 ohmio, maka resistansi ditempatkan dan arus arus ditentukan oleh yang sama.
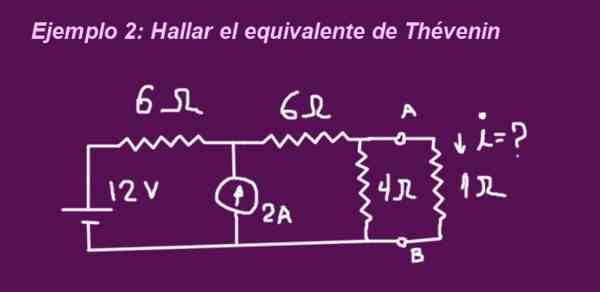Gambar 6. Contoh 2 Sirkuit. (Elaborasi sendiri) Larutan
Untuk menemukan resistansi yang setara, resistansi beban dihapus (dalam hal ini dari 1 ohmio). Selain itu, sumber tegangan digantikan oleh sirkuit pendek dan sumber arus dengan sirkuit terbuka.
Dengan cara ini, sirkuit yang akan dihitung resistansi setara adalah yang ditunjukkan di bawah ini:
Dapat melayani Anda: Boltzmann Constant: Sejarah, Persamaan, Perhitungan, Latihan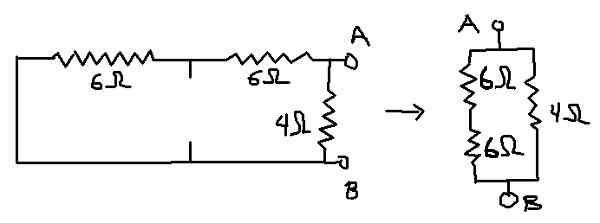
Gambar 7. Detail untuk Perhitungan Resistansi Setara (Elaborasi Sendiri) Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω yang merupakan resistansi setara thevenin (RTH).
Contoh 2B
Hitung tegangan setara Thévenin.
Larutan
Untuk menghitung tegangan setara thévenin, kami mempertimbangkan sirkuit berikut, di mana kami akan menempatkan arus di I1 dan I2 di cabang yang ditunjukkan pada gambar berikut:
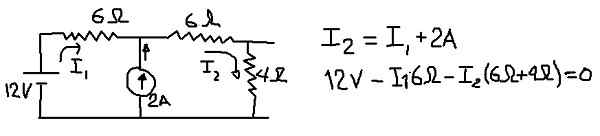Angka 8. Detail untuk Perhitungan Ketegangan Thévenin. (Elaborasi sendiri) Pada gambar sebelumnya persamaan node saat ini dan persamaan ketegangan ditunjukkan ketika mesh eksternal dilalui. Dari persamaan kedua I1 saat ini dibersihkan:
I1 = 2 - I2*(5/3)
Persamaan ini diganti dalam persamaan node:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> i2 = 12/8 = 1.5 a
Ini berarti bahwa penurunan ketegangan dalam resistansi 4 ohm adalah 6 volt.
Singkatnya, ketegangan Thévenin adalah VTH = 6 V.
Contoh 2C
Temukan sirkuit setara thevenin dan arus dalam resistansi beban.
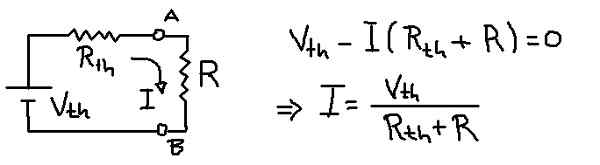Gambar 9. Arus beban dengan setara dengan thévenin. (Elaborasi sendiri) Larutan
Gambar sebelumnya menunjukkan sirkuit setara thévenin dengan resistansi beban r. Dari persamaan tegangan di mesh arus I yang beredar melalui resistansi beban r disimpulkan.
I = VTH / (RTH + R) = 6V / (3Ω + 1Ω) = 1.5 a
Penerapan Teorema Thévenin (Bagian III)
Pada bagian ketiga dari aplikasi teorema Thévenin ini, sirkuit arus bergantian berisi sumber tegangan bergantian, kondensor, induktansi dan resistansi dipertimbangkan.
Contoh 3
Tujuannya adalah untuk menemukan sirkuit Thévenin yang setara dari sirkuit berikut:
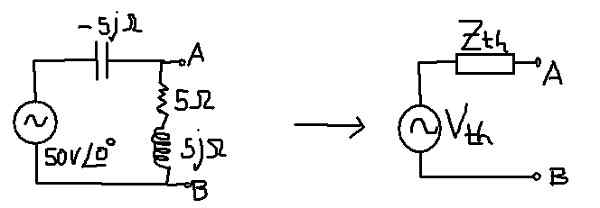Gambar 10. Thévenin di sirkuit arus bergantian. (Elaborasi sendiri) Larutan
Impedansi yang setara sesuai dengan kondensor secara paralel dengan kombinasi Seri Resistance dan Inductance.
Kebalikan dari impedansi yang setara diberikan oleh:
Zeq^-1 = (-5j)^-1 + (5 + 5j)^-1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3/ 10 J) MHO
Dan impedansi yang setara kemudian akan menjadi:
Zeq = (1 - 3 j) ohm
Arus kompleks saya dapat disimpulkan dari persamaan mesh:
50v∠0 - i (-5 j + 5 + 5j) = 50v∠0 - i*5 = 0 ===> i = 10a ∠0
Sekarang penurunan tegangan dalam resistansi plus induktansi dihitung, yaitu, tegangan VAB yang akan menjadi ketegangan setara dari thévenin:
Vab = i * (5 + 5 j) Ω = 10a ∠0 * 5Ω∠45º = 50V∠45º
Dengan kata lain
Referensi
- Tutorial Elektronik, Teorema Thevenin. Pulih dari: elektronik-tormales.WS
- Pertanyaan dan Jawaban Teori Jaringan. Teorema Thevenin. Pulih dari: sanfoundry.com
- Teorema Thevenin. Prosedur langkah demi langkah. Dipulihkan dari: Teknologi Listrik.org
- Teorema Thevenin. Contoh terpecahkan langkah demi langkah. Diperoleh dari: ElecticalSimple.Blogspot.com
- Lokakarya tentang Teorema THEVENIN DAN NORTON. Diperoleh dari: web.IIT.Edu
- Wikipedia. Teorema Thévenin. Pulih dari: wikipedia.com