Teorema Varignon

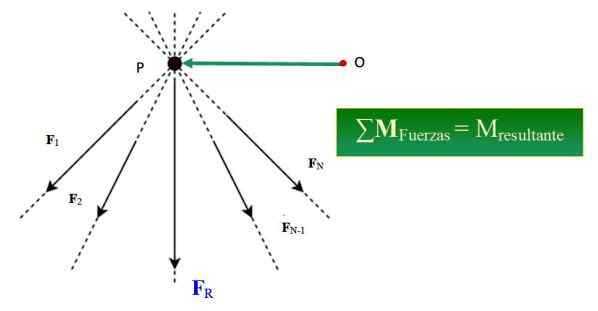
Gambar 1.- Teorema Varignon menegaskan bahwa jumlah momen kekuatan di sekitar titik tertentu setara dengan waktu hasil sehubungan dengan titik itu. Sumber: Wikimedia Commons/F. Zapata.

Apa itu Teorema Varignon?

Teorema Varignon, dalam mekanika, menyatakan bahwa jumlah momen yang dihasilkan oleh sistem kekuatan bersamaan sehubungan dengan titik tertentu, sama dengan momen gaya yang dihasilkan sehubungan dengan titik yang sama.

Karena alasan ini teorema ini juga dikenal sebagai Awal momen.

Sementara yang pertama menyatakan itu adalah orang Belanda Simon Stevin (1548-1620), pencipta paradoks hidrostatik, ahli matematika Prancis Pierre Varignon (1654-1722) adalah orang yang kemudian memberinya bentuk definitifnya.

Contoh bagaimana Teorema Varignon bekerja dalam mekanika adalah sebagai berikut: Misalkan sistem sederhana dari dua coplanares dan kekuatan bersamaan bertindak pada suatu titik F₁ Dan F₂, (Dilambangkan dengan huruf tebal untuk karakter vektornya). Kekuatan -kekuatan ini menimbulkan kekuatan jaring atau yang dihasilkan, disebut F_R.

Setiap gaya memberikan torsi atau momen sehubungan dengan titik atau, yang dihitung dengan produk vektor antara vektor posisi R_Op dan Strengh F, Di mana R_Op Itu diarahkan dari atau ke titik konkurensi P:

M_O1 = R_Op × F₁

M_O2 = R_Op × F₂

Mengingat F_R = F₁ + F₂, Jadi:

M_{SALAH SATU} = R_Op × F₁ + R_Op × F₂ = M_O1 + M_O2

tapi bagaimana caranya R_Op Maka, ini adalah faktor umum yang menerapkan properti distributif untuk produk silang:

M_{SALAH SATU} = R_Op × (F₁ + F₂) = R_Op × F_R                

Oleh karena itu, jumlah momen atau torsi masing -masing gaya sehubungan dengan titik atau setara dengan waktu gaya yang dihasilkan sehubungan dengan titik yang sama.

Pernyataan dan demonstrasi

Menjadi sistem n kekuatan bersamaan, dibentuk oleh F₁, F₂, F₃.. F_N, yang garis tindakannya dimaksudkan pada titik P (lihat Gambar 1), momen sistem kekuatan ini M_{SALAH SATU}, Tentang suatu titik atau diberikan oleh:

Dapat melayani Anda: keseimbangan yang tidak stabil: konsep dan contoh

M_{SALAH SATU} = R_Op × F₁ + R_Op × F₂ + R_Op × F₃ +.. R_Op × F_N = R_Op × (F₁ + F₂ + F₃ +.. F_N)

Demonstrasi

Untuk menunjukkan teorema, properti distributif produk vektor antara vektor dibuat.

Menjadi kekuatan F₁, F₂, F₃.. F_N diterapkan pada poin ke₁, KE₂, KE₃… KE_N dan bersamaan pada titik p. Momen yang dihasilkan dari sistem ini, sehubungan dengan suatu titik atau, disebut M_{SALAH SATU}, Ini adalah jumlah momen dari masing -masing kekuatan, sehubungan dengan titik itu:

M_{SALAH SATU} = ∑ R_Oai × F_yo

Dimana jumlahnya berubah dari i = 1 ke i = n, karena ada n pasukan. Karena ini adalah kekuatan bersamaan dan karena produk vektor antara vektor paralel adalah nol, kebetulan:

R_Pai × F_yo = 0

Dengan vektor nol dilambangkan 0.

Momen salah satu kekuatan tentang O, misalnya kekuatan F_yo diterapkan dalam a_yo, Itu ditulis seperti ini:

M_{saya dengar} = R_Oai × F_yo

Vektor posisi R_Oai  Itu dapat dinyatakan sebagai jumlah dari dua posisi vektor:

R_Oai = R_Op + R_Pai

Dengan cara ini, momen yang berkaitan dengan atau memaksa F_yo adalah:

M_{saya dengar} = (R_Op + R_Pai) × F_yo = (R_Op × F_yo) + (R_Pai × F_yo)

Tetapi istilah terakhir adalah nol, seperti yang dijelaskan di atas, karena R_Pai berada di garis aksi F_yo, Karena itu:

M_{saya dengar} = R_Op × F_yo

Mengetahui bahwa momen sistem sehubungan dengan titik atau merupakan jumlah dari semua momen individu dari setiap kekuatan sehubungan dengan titik itu, lalu:

M_{SALAH SATU} = ∑ M_{saya dengar} = ∑ R_Op × F_yo

Sebagai R_Op Itu konstan keluar dari jumlah:

M_{SALAH SATU} = R_Op × (∑ F_yo)

Tapi ∑ F_yo Itu hanyalah jaring atau kekuatan yang dihasilkan F_R, Oleh karena itu segera disimpulkan bahwa:

Dapat melayani Anda: Leyden Bottle: Bagian, Operasi, Eksperimen

M_{SALAH SATU} = R_Op × F_R

Contoh

Teorema Varignon memfasilitasi perhitungan momen kekuatan F Mengenai titik atau struktur yang ditunjukkan pada gambar, jika gaya dipecah menjadi komponen persegi panjang dan momen masing -masing dihitung:

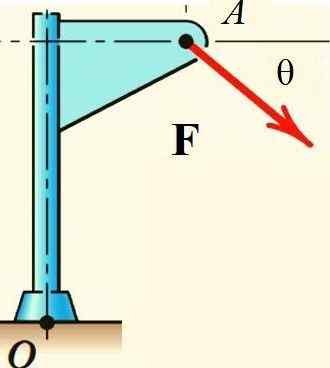Gambar 2.- Teorema Varignon berlaku untuk menghitung momen kekuatan di sekitar atau. Sumber: f. Zapata.

Aplikasi Teorema Varignon

Ketika kekuatan yang dihasilkan dari suatu sistem diketahui, teorema Varignon dapat diterapkan untuk menggantikan jumlah masing -masing momen yang dihasilkan oleh gaya yang menyusunnya pada saat hasil yang dihasilkan.

Jika sistem terdiri dari kekuatan pada bidang yang sama dan titik sehubungan dengan yang ingin Anda hitung momen milik bidang itu, momen yang dihasilkan tegak lurus.

Misalnya, jika semua kekuatan berada di bidang XY, momen tersebut diarahkan pada sumbu z dan hanya tetap menemukan besarnya dan maknanya, seperti kasus contoh yang dijelaskan di atas.

Dalam hal ini, teorema Varignon memungkinkan untuk menghitung momen yang dihasilkan dari sistem melalui penjumlahan. Ini sangat berguna dalam kasus sistem kekuatan tiga dimensi, yang arah momen yang dihasilkan tidak diketahui apriori.

Untuk menyelesaikan latihan ini, itu nyaman.

Olahraga diselesaikan

Dengan teorema Varignon, hitung momen gaya F di sekitar titik atau ditunjukkan pada gambar jika besarnya F adalah 725 N.

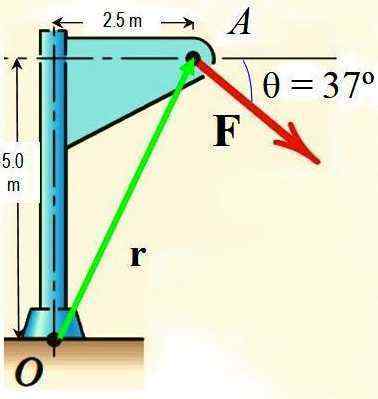Gambar 3.- Gambar untuk latihan diselesaikan. Sumber: f. Zapata.

Larutan

Untuk menerapkan teorema Varignon, paksa terurai F dalam dua komponen, yang momen masing -masing di sekitar atau dihitung dan ditambahkan untuk mendapatkan momen yang dihasilkan.

Dapat melayani Anda: tubuh yang kaku

F_X = 725 n ∙ cos 37 º = 579.0 n

F_Dan = - 725 n n ∙ sen 37 º = −436.3 n

Demikian pula, vektor posisi R diarahkan dari atau ke A memiliki komponen:

R_X = 2.5m

R_Dan = 5.0 m

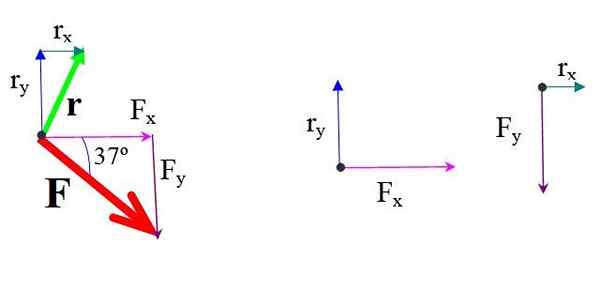Gambar 4.- Komponen kekuatan dan posisi. Sumber: f. Zapata.

Momen dari setiap komponen gaya sehubungan dengan atau mengalikan gaya dan jarak tegak lurus.

Kedua kekuatan cenderung memutar struktur dalam arah yang sama, yang dalam hal ini adalah indera skor, yang secara sewenang -wenang diberi tanda positif:

M_Sapi = F_X∙ r_Dan ∙ sin 90º = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_Dan∙ r_X ∙ sin (−90º) = −436.3 n ∙ 2.5 m ∙ (−1) = 1090.8 n ∙ m

Momen yang dihasilkan sehubungan dengan atau adalah:

M_{SALAH SATU} = M_Sapi + M_Oy = 3985.8 n ∙ m tegak lurus terhadap pesawat dan torsi.

Referensi

1. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley. 
2. Bir, f. 2010. Statis. Bukit McGraw. 9NA. Edisi.
3. Hibbeler, R. 1992. Mekanika untuk Insinyur. 6. Edisi. CECSA.
4. HK Engineering. Teorema Varignon. Dipulihkan dari: YouTube.com.
5. Wikipedia. Teorema Varignon (Mekanika). Diperoleh dari: di.Wikipedia.org.