Teorema Faktor Penjelasan, Contoh, Latihan

Dia Teorema Faktor menyatakan bahwa polinomial p (x) dapat dibagi dengan binomial bentuk (x - a) jika x = a adalah akar p (x), yaitu p (a) = 0. Dikatakan bahwa polinomial dapat dibagi di antara yang lain ketika residu atau istirahatnya adalah nol.

Polinomial adalah ekspresi bentuk:

P (x) = a_N X^N + ke_N-1 X^N-1 +... + a₁ x + a₀

Gambar 1. Teorema Faktor. Sumber: f. Zapata.

Di mana:

-n adalah tingkat polinomial, menjadi nomor integer terbesar yang menjadi variabel independen x naik,

-Nilai a_N, ke_N-1 ,... + a₁ , ke₀ Mereka adalah koefisien polinomial, yang umumnya bilangan real, tetapi mereka juga bisa menjadi bilangan kompleks.

Polinomial grade N dapat terurai sebagai produk bentuk binomial:

(X - r_yo)

Dimana r_yo Ini adalah root p (x) i-alkish:

P (x) = a_N (X - r₁) (X - r₂) ... (x - r_N)

Karena jumlah akar polinomial sama dengan tingkat yang sama.

[TOC]

Contoh

- Contoh 1

Pertimbangkan polinomial menurut kasus:

P (x) = 3⋅x² - 7⋅x + 2

Anda ingin tahu apakah polinomial ini dapat dibagi oleh binomial (x - 2). Jika teorema faktor digunakan, maka kita harus mengevaluasi p (x = 2) untuk mengetahui apakah nilai 2 adalah root atau tidak. Kami kemudian melanjutkan untuk mengevaluasi ekspresi:

P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.

Ternyata x = 2 adalah p (x) root, jadi menurut teorema faktor, binomial (x - 2) memang merupakan faktor p (x).

Mari beralih ke verifikasi langsung membuat divisi. Detail tentang bagaimana divisi dibuat ditunjukkan pada gambar berikut:

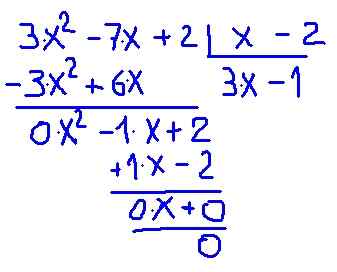Gambar 2.- Divisi Polinomial P (x) antara binomial X-2. Sumber: f. Zapata.

Diverifikasi bahwa hasil bagi antara p (x) dan (x -2) memberikan polinomial derajat kecil yang disebut hasil bagi C (x) = 3⋅x - 1 dengan residu 0.

Dapat melayani Anda: fungsi vektor

Kita dapat meringkas hasilnya sebagai berikut:

(3⋅x² - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0

Ekspresi sebelumnya dapat ditulis dengan cara lain, hanya mengingat bahwa dividen p (x) sama dengan produk pembagi (x -2) oleh hasil bagi (3⋅x - 1) ditambah residu (nol dalam kasus ini ):

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0

Dengan cara ini, polinomial P (x) (x), yaitu, tulis sebagai produk polinomial, polinomial asli: polinomial asli:

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1)

- Contoh 2

Menjadi q polinomial (x) = x³ - x + 2. Anda ingin tahu apakah itu dapat dibagi oleh binomial (x + 1).

Cara yang paling langsung adalah dengan menerapkan teorema faktor. Dalam hal ini Anda hanya perlu memverifikasi apakah x = -1 membatalkan atau tidak q polinomial (x).

Kami melanjutkan dengan mengganti:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Hasilnya berbeda dari nol, oleh karena itu teorema faktor memastikan bahwa q polinomial tidak dapat dibagi antara (x + 1), karena q (-1) ≠.

Sekarang pembagian Q (x) akan dibuat antara binomial (x + 1) sebagai metode verifikasi kesimpulan kami.

Pada kesempatan ini, divisi akan dilakukan melalui metode divisi sintetis, yang terdiri dari penempatan di baris atas kelas satu semua koefisien polinomial, termasuk yang hilang, karena mereka tidak memiliki koefisien nol koefisien.

Kemudian di kolom pertama istilah independen pembagi ditempatkan tetapi dengan tanda diubah, dalam kasus kami pembagi adalah (x + 1). Istilah independennya adalah 1, tetapi seperti pada kolom pertama ditempatkan tanda yang diubah, yaitu -1.

Gambar berikut menggambarkan bagaimana divisi sintetis dilakukan:

Dapat melayani Anda: persamaan polinomial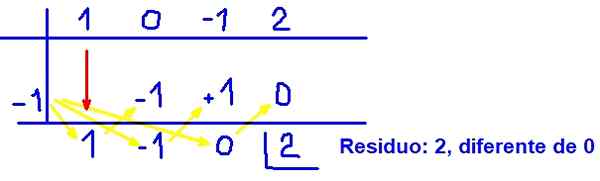Gambar 3. Contoh Divisi Sintetis Polinomial. Sumber: f. Zapata.

Dengan hasil ini terbukti bahwa (x + 1) itu bukan faktor polinomial q (x) = x³ - x + 2 Karena residu tidak nol.

Kesimpulan ini tidak terkejut, karena sudah diprediksi dengan teorema faktor. Perhatikan bahwa saat mengganti x = -1 dalam q (x) Apa yang diperoleh justru residu atau sisa divisi polinomial, karena q (-1) = residu = 2.

Tentu saja, Divisi memberikan informasi tambahan tentang hasil bagi C (x) = x² - X.

Mengingat bahwa dividen Q (x) sama dengan pembagi (x + 1) dengan rasio C (x) ditambah residu r = 2 kita memiliki perluasan q polinomial sebagai berikut:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

Perlu dicatat bahwa ekspresi ini bukan faktorisasi polinomial tersebut, karena ada penambahan istilah non -non -non -non -non -non -non.

Latihan

- Latihan 1

Temukan faktor polinomial

P (x) = x³ - 5 x² + 2 x + 8

Dan juga menulis faktorisasi Anda.

Larutan

Teorema faktor menunjukkan bahwa kita harus mencari akarnya ke dan kemudian temukan faktor (x - ke), Dalam hal ini, karena merupakan polinomial kelas tiga, harus ada tiga akar. 

Karena ini adalah polinomial dengan seluruh koefisien, akarnya harus menjadi salah satu pembagi istilah independen yang dalam hal ini adalah 8. Pembagi ini adalah:

± 1, ± 2, ± 4, ± 8.

Kita mulai dengan menjelajahi +1: p (+1) = 1³ - 5⋅ 1² + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6 yang berbeda dari 0, oleh karena itu +1 bukan root.

Kami menjelajahi -1:

P (-1) = (-1)³ - 5⋅ (-1)² + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0

Dari hasil disimpulkan bahwa -1 adalah akar p (x) y (x -( -1)) = (x + 1) adalah faktor polinomial.

Dapat melayani Anda: kotak minimum

Kita perlu menemukan dua faktor lagi:

Kami mencoba yang berikutnya +2:

P (+2) = (+2)³ - 5⋅ (+2)² + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Sekali lagi kami mendapat nol. Maka faktor lainnya adalah (x - 2).

Karena itu adalah polinomial kelas tiga, kita hanya perlu menemukan faktor. Sekarang kami mencoba nilai +4 untuk mengetahui jika polinomial membatalkan:

P (+4) = (+4)³ - 5⋅ (+4)² + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Dengan kata lain.

Anda tidak harus terus mencari, karena itu adalah polinomial kelas 3 yang memiliki tiga akar paling banyak. Dalam latihan ini semua akar ternyata nyata dan utuh.

Oleh karena itu P polinomial (x) adalah faktor seperti ini:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Latihan 2

Jadilah polinomial p⋅x³ - x + 2p. Tentukan nilai P untuk polinomial agar dapat dibagi dengan (x + 2).

Larutan

Kami menggunakan teorema faktor, yang menyatakan bahwa jika x = -2 membatalkan polinomial maka (x -( -2)) adalah faktor dari polinomial tersebut.

Kemudian X digantikan oleh (-2) dalam polinomial asli, disederhanakan dan sama dengan nol:

P⋅ (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Sekarang nilai P dibersihkan sehingga kesetaraan dipenuhi ke nol:

P = -2 / 10 = -⅕ 

Ini berarti polinomial itu: 

-⅕⋅x³ - X - ⅖

Itu dapat dibagi dengan (x + 2), atau apa yang setara: (x + 2) adalah salah satu faktornya.

Referensi

1. Baldor Aurelio. Aljabar. Grup Editorial Patria.
2. Demana, w. Precáculculo: grafik, numerik, edisi ke -7 aljabar. Pendidikan Pearson.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.