Matematika

Teselados Karakteristik, Jenis (Reguler, Tidak Teratur), Contoh

Teselados Karakteristik, Jenis (Reguler, Tidak Teratur), Contoh

Itu Tesselled Mereka adalah permukaan yang ditutupi oleh satu atau lebih figur yang disebut Tessels. Mereka ada di mana -mana: di jalanan dan bangunan dari semua jenis. Tessels atau ubin adalah potongan datar, biasanya poligon dengan salinan kongruen atau isometrik, yang ditempatkan mengikuti pola reguler. Dengan cara ini tidak ada ruang tanpa tertutup dan ubin atau mosaik tidak tumpang tindih. 

Dalam hal satu jenis mosaik yang dibentuk oleh poligon biasa digunakan maka ada a Tesseld biasa, Tetapi jika dua atau lebih jenis poligon biasa digunakan, maka itu adalah a Tesselled semi -reguler.

Gambar 1. Lantai lantai ubin tidak beraturan, karena persegi panjang adalah poligon non-reguler, bahkan saat kotak. Sumber: Pixabay.

Akhirnya ketika poligon yang membentuk Tesseldo tidak teratur, jadi itu adalah a Tesselled tidak teratur.

Jenis Tesseldo yang paling umum adalah yang dibentuk oleh mosaik persegi panjang dan khususnya persegi. Pada Gambar 1 kami memiliki contoh yang baik.

[TOC]

Sejarah Teselados

Tessellation telah digunakan selama ribuan tahun untuk menutupi lantai dan dinding istana dan kuil budaya dan agama yang berbeda.

Misalnya, peradaban Sumeria yang berkembang sekitar 3500 menjadi.C. Di sebelah selatan Mesopotamia, antara Sungai Efrat dan Tigris, mereka menggunakan Tesel dalam arsitektur mereka.

Gambar 2. Teselados Sumerios di pintu Istar. Sumber: Wikimedia Commons.

Tesels juga membangkitkan minat ahli matematika sepanjang masa: dimulai dengan Archimedes pada abad ketiga SM, diikuti oleh Johannes Kepler pada tahun 1619, Camille Jordan pada tahun 1880, hingga zaman kontemporer dengan Roger Penrose.

Itu dapat melayani Anda: fraksi setara dengan 3/5 (solusi dan penjelasan)

Penrose menciptakan tessellation non -periodik yang dikenal sebagai Tessellation Penrose. DANini Mereka hanyalah beberapa nama ilmuwan yang berkontribusi banyak tentang tessellation.

Tesel biasa

Teslate biasa dibuat dengan satu jenis poligon biasa. Di sisi lain, sehingga Tesseldo dapat dianggap biasa semua titik pesawat harus:

-Milik interior poligon

-Atau ke tepi dua poligon yang berdekatan 

-Akhirnya, itu bisa menjadi milik simpul umum dari setidaknya tiga poligon.

Dengan pembatasan di atas dapat ditunjukkan bahwa hanya segitiga sama sisi, kotak dan segi enam dapat membentuk tessel biasa.

Tata nama

Ada nomenklatur untuk menunjukkan taring yang terdiri dari daftar ke arah jarum jam dan dipisahkan oleh suatu titik, jumlah sisi poligon yang mengelilingi setiap node (atau simpul) dari tesselled, selalu dimulai dengan angka terkecil sisi.

Nomenklatur ini berlaku untuk Tesselves reguler dan semi -reguler. 

Contoh 1: Teselado Triangular

Gambar 3 menunjukkan ubin reguler segitiga. Perlu dicatat bahwa setiap simpul ubin segitiga adalah simpul umum dari enam segitiga sama sisi. 

Cara menunjukkan jenis tesseldo ini adalah 3.3.3.3.3.3, yang juga dilambangkan dengan 36.

Gambar 3. Teselado 3 Triangular Reguler.3.3.3.3.3. Sumber: Wikimedia Commons

Contoh 2: Square Tessel

Gambar 4 menunjukkan ubin biasa hanya terdiri dari kotak. Perlu dicatat bahwa setiap simpul ubin dikelilingi oleh empat kotak kongruen. Notasi yang berlaku untuk jenis tesselves persegi ini adalah: 4.4.4.4 o Bergantian 44

Gambar 4. Square Tesseld 4.4.4.4. Sumber: Wikimedia Commons.

Contoh 3: Tesseld heksagonal

Di tesselle heksagonal. Nomenklatur untuk tesselled heksagonal biasa adalah 6.6.6 o Bergantian 63.

Dapat melayani Anda: bagian kerucut: jenis, aplikasi, contoh Gambar 5. Hexagonal Tesseld 6.6.6. Sumber: Wikimedia Commons.

Tesselled semi -reguler

Tesel semi -reguler atau tesselled dari Archimedes terdiri dari dua atau lebih jenis poligon biasa. Setiap simpul dikelilingi oleh jenis -jenis poligon yang membentuk tessellated dalam urutan yang sama dan kondisi tepi yang sepenuhnya dibagikan dengan tetangga dipertahankan.

Ada delapan kerucut semi -reguler:

  1. 3.6.3.6 (tri-hexagonal tesselled)
  2. 3.3.3.3.6 (Hexagonal Teslate Romo)
  3. 3.3.3.4.4 (Teselado segitiga Elongado)
  4. 3.3.4.3.4 (Romo Square Tesselled)
  5. 3.4.6.4 (Rombi-tri-hexagonal Tesseld)
  6. 4.8.8 (Tesselled persegi terpotong)
  7. 3.12.12 (Tesseld heksagonal terpotong)
  8. 4.6.12 (Tesseld tri-hexagonal terpotong)

Beberapa contoh teslate semi -reguler ditunjukkan di bawah ini.

Contoh 4: Tixagonal Teselado

Ini adalah salah satu yang terdiri dari segitiga sama sisi reguler dalam Struktur 3.6.3.6, yang berarti bahwa simpul ubin dikelilingi (sampai menyelesaikan pengembalian) dengan segitiga, seekor segi enam, segitiga dan seekor segi enam. Gambar 6 menunjukkan tessel seperti itu.

Gambar 6. Tesseld Tri-Hexagonal (3.6.3.6) Ini adalah contoh semi -reguler Tesselled. Sumber: Wikimedia Commons.

Contoh 5: Hexagonal Tesseldo Romo

Seperti ubin contoh sebelumnya, ini juga terdiri dari segitiga dan segi enam, tetapi distribusinya di sekitar node adalah 3.3.3.3.6. Gambar 7 dengan jelas menggambarkan jenis tesselled ini.

Gambar 7. Hexagonal Tesseldo Romo terdiri dari segi enam yang dikelilingi oleh 16 segitiga dalam konfigurasi 3.3.3.3.6. Sumber: Wikimedia Commons.

Contoh 6: Tessel Rombi-Tri-Hexagonal

Ini adalah ubin yang terdiri dari segitiga, kotak, dan segi enam, dalam konfigurasi 3.4.6.4, yang ditunjukkan pada Gambar 8.

Angka 8. Tesselled semi -reguler terdiri dari segitiga, persegi dan segi enam dalam konfigurasi 3.4.6.4. Sumber: Wikimedia Commons.

Tesel tidak teratur

Mereka disebut hancur tidak beraturan dengan yang dibentuk oleh poligon yang tidak teratur, atau oleh poligon biasa tetapi yang tidak memenuhi kriteria bahwa simpul adalah simpul dari setidaknya tiga poligon.

Itu dapat melayani Anda: antiderivatif: rumus dan persamaan, contoh, latihan

Contoh 7

Gambar 9 menunjukkan contoh ubin tidak teratur, di mana semua poligon teratur dan kongruen. Ini tidak teratur karena simpul bukanlah simpul umum dari setidaknya tiga kotak dan ada juga kotak tetangga yang tidak sepenuhnya berbagi tepi.

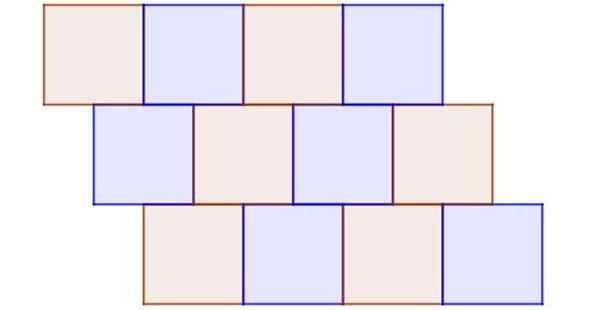Gambar 9. Bahkan ketika semua ubin adalah kotak kongruen, ini adalah contoh yang jelas dari tesselled yang tidak teratur. Sumber: f. Zapata.

Contoh 8

Jajaran genjang ini adalah permukaan yang rata, tetapi kecuali jika persegi tidak dapat membentuk tessel biasa.

Gambar 10. Tesseldo yang dibentuk oleh jajaran genjang tidak teratur, karena mosaiknya adalah poligon non -reguler. Sumber: f. Zapata.

Contoh 9

Heksagon non-reguler dengan simetri pusat mengatur permukaan datar, seperti yang ditunjukkan pada gambar berikut:

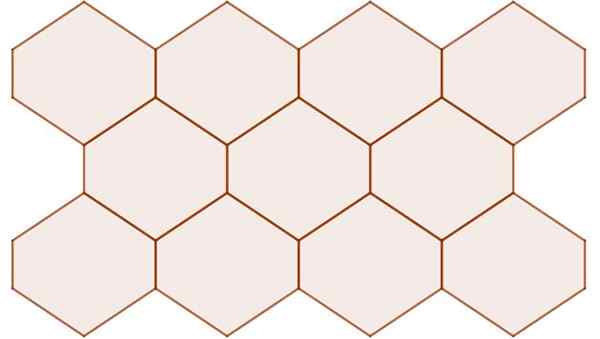Gambar 11. Hexagon dengan simetri pusat bahkan ketika mereka tidak biasa mereka mengatur pesawat. Sumber: f. Zapata.

Contoh 10: El Cairo Teselado

Ini adalah tessellation yang sangat menarik, terdiri dari pentagon dengan sisi dengan panjang yang sama tetapi dengan sudut yang tidak setara, dua di antaranya lurus dan tiga lainnya memiliki 120º masing -masing.

Namanya datang bahwa Tesseld ini ada di trotoar beberapa jalan di Kairo di Mesir. Gambar 12 menunjukkan Tesseldo dari Kairo.

Gambar 12. Kairo Tesseldo. Sumber: Wikimedia Commons.

Contoh 11: Teselado al-Andalus

Tesseldo Selama beberapa bagian Andalusia dan Afrika Utara ditandai dengan geometri dan epigrafi, selain unsur -unsur hias seperti vegetasi. 

Tesselled Palacios seperti Alhambra yang terdiri dari ubin yang dibentuk oleh potongan -potongan keramik dari banyak warna, dengan banyak bentuk (bukan yang tak terbatas) yang memicu plot geometris.

Gambar 13. Teselado Palacio de la Alhambra. Tartaglia / domain publik

Contoh 12: Teselado di Videogues

Juga dikenal sebagai Tesellation, ini adalah salah satu yang paling ledakan dalam video game. Ini adalah penciptaan tekstur untuk mensimulasikan tesseld dari berbagai skenario yang muncul di simulator.

Ini adalah refleksi yang jelas bahwa penutup ini terus berkembang dengan mentransfer perbatasan realitas.

Referensi

  1. Nikmati matematika. Tesel. Pulih dari: nikmatiMaticaticas.com
  2. Rubiños. Tesels menyelesaikan contoh. Pulih dari: matematika.Blogspot.com
  3. Weisstein, Eric W. "Deiregula Tessellation". Weisstein, Eric W, Ed. Mathworld. Penelitian Wolfram.
  4. Wikipedia. Tesselled. Pulih dari: is.Wikipedia.com
  5. Wikipedia. Tesseld biasa. Pulih dari: is.Wikipedia.com