Karakteristik segitiga Balacket, properti, rumus, area

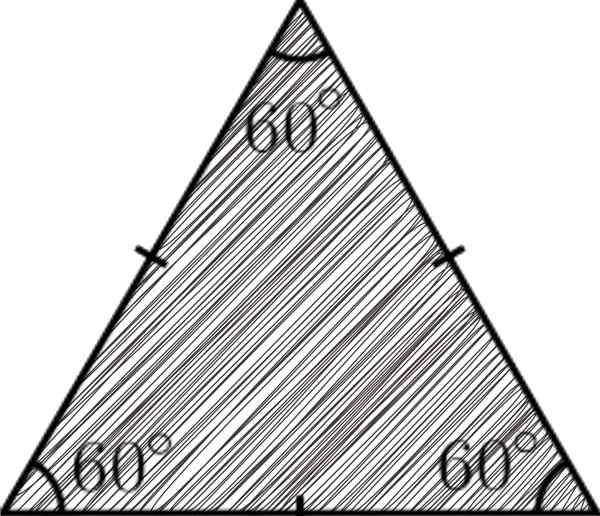
A segitiga sama sisi Ini adalah poligon tiga sisi, di mana semuanya sama; yaitu, mereka memiliki ukuran yang sama. Untuk karakteristik itu diberi nama sama sisi (sisi yang sama).

Segitiga adalah poligon dianggap sebagai yang paling sederhana dalam geometri, karena tiga sisi, tiga sudut dan tiga simpul terbentuk. Dalam kasus segitiga sama sisi, untuk memiliki sisi yang sama, itu menyiratkan bahwa tiga sudutnya juga akan.

Contoh segitiga sama sisi

[TOC]

Karakteristik segitiga keseimbangan

- Sisi yang sama

Segitiga sama sisi adalah figur datar dan tertutup, terdiri dari tiga garis garis. Segitiga diklasifikasikan berdasarkan karakteristiknya, dalam kaitannya dengan sisi dan sudutnya; Puilateral diklasifikasikan menggunakan ukuran sisi mereka sebagai parameter, karena ini persis sama, yaitu, mereka kongruen.

Segitiga sama sisi adalah kasus khusus dari segitiga samaan karena dua sisinya kongruen. Itulah sebabnya semua segitiga sama sisi juga merupakan Isosceles, tetapi tidak semua segitiga Isosceles akan menjadi sama sisi.

Dengan cara ini segitiga sama sisi memiliki sifat yang sama dari segitiga isosceles.

Segitiga sama sisi juga dapat diklasifikasikan oleh amplitudo sudut internal mereka sebagai segitiga akut ekuilateral, yang memiliki ketiga sisi dan tiga sudut internal dengan ukuran yang sama. Sudut akan akut, yaitu, mereka akan kurang dari 90^{salah satu}.

- Komponen

Segitiga secara umum memiliki beberapa baris dan titik yang menyusunnya. Mereka digunakan untuk menghitung area, sisi, sudut, median, bisector, mediatrix dan tinggi.

• Mediannya: Ini adalah garis yang pergi dari titik tengah di satu sisi dan mencapai titik yang berlawanan. Tiga media hadir pada titik yang disebut Baricentro atau Centroid.
• The Bisector: Ini adalah semi -benar yang membagi sudut simpul menjadi dua sudut dengan ukuran yang sama, sehingga dikenal sebagai sumbu simetri. Segitiga sama sisi memiliki tiga sumbu simetri. Dalam segitiga sama sisi, bisektor diambil dari titik sudut ke sisi yang berlawanan, memotongnya ke titik tengahnya. Anda berada di titik yang disebut Insenter.
• Mediatrix: Ini adalah segmen tegak lurus terhadap sisi segitiga yang berasal dari tengah ini. Ada tiga mediatik dalam segitiga dan mereka setuju pada titik yang disebut circumcentro.
• Tinggi: Ini adalah garis yang bergerak dari simpul ke sisi yang berlawanan dan juga garis ini tegak lurus ke sisi itu. Semua segitiga memiliki tiga ketinggian yang bertepatan pada suatu titik yang disebut Ortotenter.

Dalam grafik berikut kami mengamati segitiga scalene di mana beberapa komponen yang disebutkan di atas terperinci

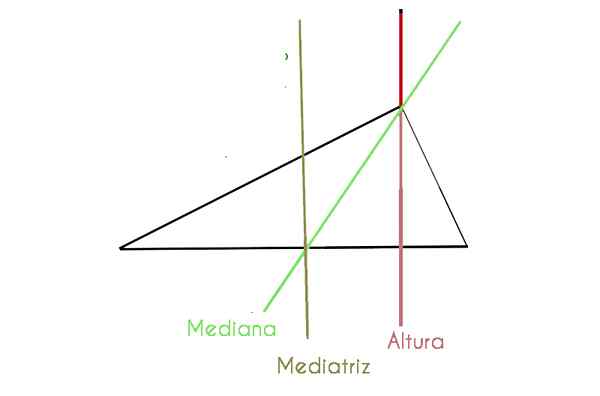Kita dapat dengan jelas melihat komponen, sesuatu yang lebih sulit di segitiga sama sisi, karena beberapa bertepatan. Kami menjelaskannya di bawah ini:

Para bisector, median dan mediatrix adalah kebetulan

Bisector membelah di sebelah segitiga menjadi dua bagian. Dalam segitiga sama sisi sisi itu akan dibagi menjadi dua bagian yang persis sama, yaitu segitiga akan dibagi menjadi dua segitiga persegi panjang kongruen.

Dengan demikian, bisector yang diambil dari sudut mana pun dari segitiga sama sama bertepatan dengan median dan mediatrix di sisi yang berlawanan dengan sudut itu.

Dapat melayani Anda: Hubungan Proporsionalitas: Konsep, Contoh dan Latihan

Contoh:

Gambar berikut menunjukkan segitiga ABC dengan mid d yang membagi salah satu sisi menjadi dua segmen AD dan BD.

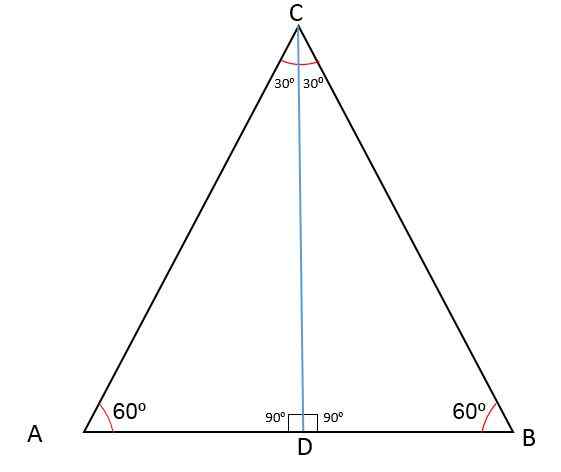
Saat menggambar garis dari titik D ke titik berlawanan, menurut definisi median CD diperoleh, yang relatif terhadap vertex C dan ke samping AB.

Karena segmen CD membagi segitiga ABC menjadi dua segitiga CDB dan CDA yang sama, itu berarti bahwa itu akan menjadi kasus kongruensi: sisi, sudut, sisi dan oleh karena itu CD juga akan menjadi BCD Bisector.

Saat menggambar segmen CD, sudut titik dibagi menjadi dua sudut yang sama dari 30^{salah satu}, Sudut titik A terus mengukur 60^{salah satu} Dan garis CD membentuk sudut 90^{salah satu} Mengenai titik tengah D.

Segmen CD membentuk sudut yang memiliki ukuran yang sama untuk segitiga ADC dan BDC, yaitu, mereka tambahan sedemikian rupa sehingga ukuran masing -masing adalah:

Med. (ADB) + Med. (ADC) = 180^{salah satu}

2 _* Med. (ADC) = 180^{salah satu}

Med. (ADC) = 180^{salah satu} ÷ 2

Med. (ADC) = 90^{salah satu}.

Maka, segmen CD juga merupakan mediatrix di sisi AB.

Bisektor dan tinggi badan adalah kebetulan

Saat bisector melacak dari simpul sudut ke titik tengah sisi yang berlawanan, ini membagi segitiga sama sisi menjadi dua segitiga kongruen yang kongruen.

Sedemikian rupa sehingga sudut 90 terbentuk^{salah satu} (lurus). Ini menunjukkan bahwa segmen garis ini benar -benar tegak lurus dengan sisi itu, dan menurut definisi garis itu akan menjadi ketinggian.

Dengan cara ini, pembagian dari setiap sudut segitiga sama sisi, bertepatan dengan tinggi relatif terhadap sisi yang berlawanan dari sudut itu.

Orocentro, Baricentro, Incentro dan Colecentro Coinsides

Karena ketinggian, median, bisector, dan mediatrix diwakili pada saat yang sama dengan segmen yang sama, dalam segitiga sama sisi, titik pertemuan segmen -segmen ini -orthocenter, baricenter, insenter, dan sunat -akan ditemukan pada titik yang sama:

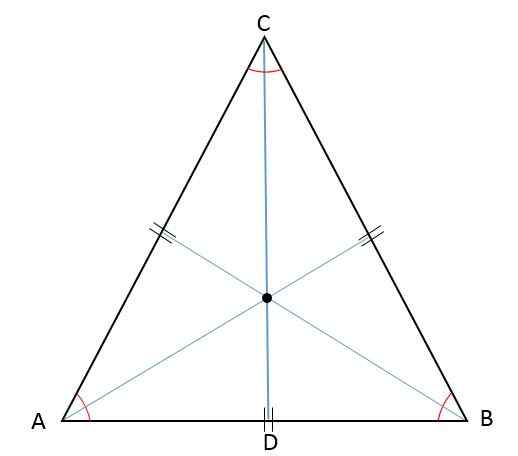
Properti

Properti utama dari segitiga sama sisi adalah bahwa mereka akan selalu menjadi segitiga isosceles, karena Isosceles dibentuk oleh dua sisi kongruen dan keseimbangan dengan tiga.

Dengan cara ini, segitiga sama sisi yang mewarisi semua sifat segitiga Isosceles:

Sudut internal

Jumlah sudut internal selalu sama dengan 180^{salah satu}, Dan karena semua sudutnya kongruen, sehingga masing -masing akan berukuran 60^{salah satu}.

Sudut eksternal

Jumlah sudut eksternal akan selalu sama dengan 360^{salah satu}, Oleh karena itu setiap sudut eksternal akan mengukur 120^{salah satu}. Itu karena sudut internal dan eksternal adalah pelengkap, yaitu, dengan menambahkannya, mereka akan selalu sama dengan 180^{salah satu}.

Jumlah sisi

Jumlah ukuran dua sisi harus selalu lebih besar dari ukuran sisi ketiga, yaitu, A + B> C, di mana A, B dan C adalah pengukuran di setiap sisi.

Sisi kongruen

Segitiga sama sisi memiliki tiga sisi dengan ukuran atau panjang yang sama; yaitu, mereka kongruen. Oleh karena itu, di item sebelumnya Anda harus = b = c.

Sudut yang kongruen

Segitiga sama sisi juga dikenal sebagai segitiga yang sama, karena tiga sudut internal mereka secara kongruen satu sama lain. Ini karena semua sisi mereka juga memiliki ukuran yang sama.

Itu dapat melayani Anda: variabel nominal: konsep dan contoh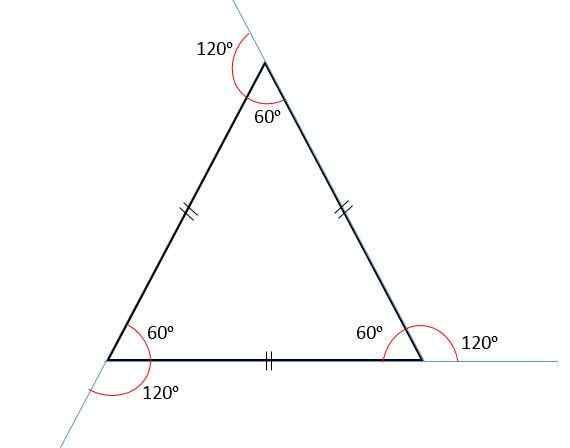

Cara menghitung perimeter?

Perimeter poligon dihitung dengan jumlah sisi. Seperti dalam hal ini segitiga sama sisi memiliki semua sisi dengan ukuran yang sama, perimeternya dihitung dengan rumus berikut:

P = 3 _* samping.

Cara menghitung ketinggian?

Karena tinggi adalah garis tegak lurus terhadap pangkalan, membaginya menjadi dua bagian yang sama dengan memanjang ke verteks yang berlawanan. Dengan demikian dua segitiga terbentuk persegi panjang yang sama.

Tinggi (h) mewakili kateto yang berlawanan (A), setengah dari sisi AC ke cateto yang berdekatan (b) dan sisi BC mewakili hipotenus (C).

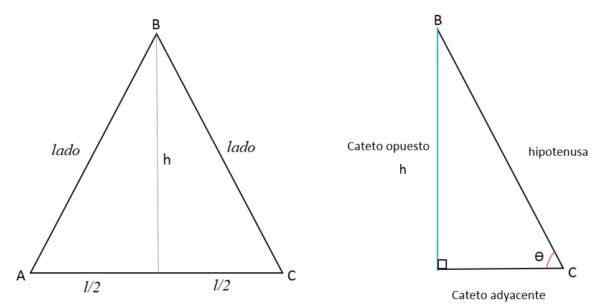
Menggunakan teorema Pythagoras, nilai ketinggian dapat ditentukan:

ke² + B² = c²

Di mana:

ke² = Tinggi (h).

B² = sisi b / 2.

C² = Sisi a.

Mengganti nilai -nilai itu dalam teorema Pythagoras, dan membersihkan ketinggian yang Anda miliki:

H² + ( L / 2)² = l²

H² +  l²/ 4 = l²

H² = l²  -  l²/ 4

H² = (4_*l² -  l²) / 4

H² =  3_*l² /4

√H² = √ (3_*l² /4)

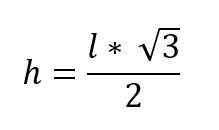
Jika sudut yang dibentuk oleh sisi kongruen, ketinggian (diwakili oleh kaki) diketahui, itu dapat dihitung dengan menerapkan alasan trigonometri.

Kategori disebut berlawanan atau berdekatan tergantung pada sudut yang diambil sebagai referensi.

Misalnya, pada gambar sebelumnya cateto h akan berlawanan dengan sudut C, tetapi berdekatan dengan sudut b:

Dengan demikian, tinggi dapat dihitung dengan:

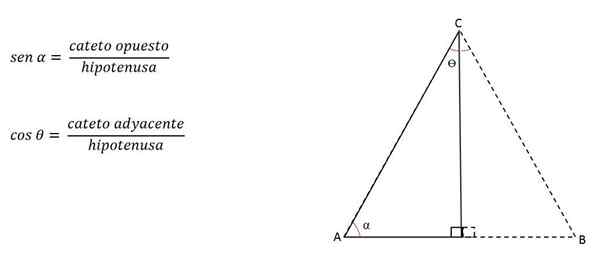
Cara Menghitung Sisi?

Ada kasus di mana ukuran sisi segitiga tidak diketahui, tetapi tinggi dan sudut yang terbentuk di simpul.

Untuk menentukan area dalam kasus ini, perlu menerapkan alasan trigonometri.

Mengetahui sudut salah satu simpulnya, kategori diidentifikasi dan alasan trigonometri yang sesuai digunakan:

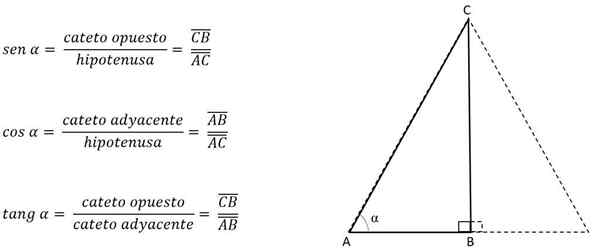
Dengan demikian, Cateto AB akan bertentangan dengan sudut C, tetapi berdekatan dengan sudut a. Tergantung pada sisi atau kaki yang sesuai dengan ketinggian, sisi lain dibersihkan untuk mendapatkan nilai ini, mengetahui bahwa dalam segitiga sama sisi ketiga sisi akan selalu memiliki ukuran yang sama.

Cara menghitung area tersebut?

Segitiga selalu dihitung dengan rumus yang sama, mengalikan pangkalan dengan tinggi dan membaginya dengan dua:

Area = (b _* H) ÷ 2

Mengetahui bahwa ketinggian diberikan oleh formula:

Latihan

- Latihan Pertama

Sisi dari segitiga sisi ABC mengukur masing -masing 20 cm. Hitung tinggi dan luas poligon itu.

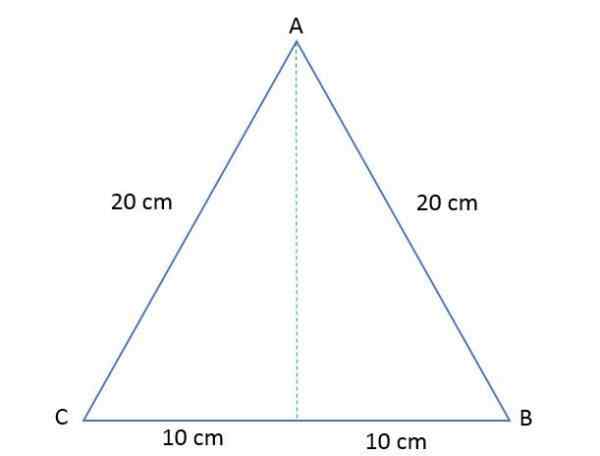
Larutan

Untuk menentukan luas segitiga sama sisi itu perlu untuk menghitung ketinggian, mengetahui bahwa ketika menggambarnya, ia membagi segitiga menjadi dua persegi panjang yang sama.

Dengan begitu Anda dapat menggunakan teorema Pythagoras untuk menemukannya:

ke² + B² = c²

Di mana:

A = 20/2 = 10 cm.

B = tinggi.

C = 20 cm.

Data diganti dalam teorema:

10² + B² = 20²

100 cm + B² = 400 cm

B² = (400 - 100) cm

B² = 300cm

B = √300 cm

B = 17,32 cm.

Yaitu, ketinggian segitiga sama dengan 17.32cm. Sekarang dimungkinkan untuk menghitung area segitiga yang diberikan dengan mengganti formula:

Area = (b _* H) ÷ 2

Area = (20 cm _* 17.32 cm) ÷ 2

Itu dapat melayani Anda: transformasi linier: properti, apa saja penggunaan, jenis, contoh

Area = 346.40 cm² ÷ 2

Area = 173,20 cm².

Cara lain yang lebih sederhana untuk menyelesaikan latihan adalah mengganti data dalam rumus langsung area, di mana nilai ketinggian juga ditemukan secara implisit:

- Latihan kedua

Di ladang yang memiliki bentuk segitiga sama sisi, bunga akan menanam. Jika perimeter medan itu sama dengan 450 m, hitung jumlah meter yang menempati bunga.

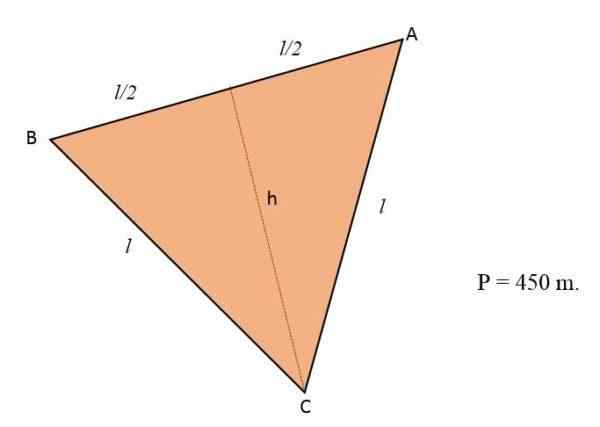
Larutan

Mengetahui bahwa perimeter segitiga sesuai dengan jumlah dari ketiga sisi dan ketika medan berbentuk seperti segitiga sama sisi, ketiga sisi ini akan memiliki ukuran atau panjang yang sama:

P = sisi + sisi + sisi = 3 _* l

3 _* l = 450 m.

L = 450 m ÷ 3

L = 150 m.

Sekarang hanya perlu untuk menghitung ketinggian segitiga itu.

Ketinggian membagi segitiga menjadi dua segitiga persegi panjang kongruen, di mana salah satu kategori mewakili ketinggian dan bagian lainnya dari pangkalan. Dengan teorema Pythagoras, ketinggian dapat ditentukan:

ke² + B² = c²

Di mana:

ke = 150 m ÷ 2 = 75 m.

C = 150 m.

B = Tinggi

Data diganti dalam teorema:

(75 m)² + B² = (150 m)²

5.625 m + B² = 22.500 m

B² = 22.500 m - 5.625 m

B² = 16.875 m

B = √16.875 m

B = 129,90 m.

Dengan demikian area yang akan ditempati bunga adalah:

Area = b * h ÷ 2

Area = (150 m _* 129,9 m) ÷ 2

Area = (19.485 m²) ÷ 2

Area = 9.742,5 m²

- Latihan ketiga

Segitiga Equilateral ABC dibagi dengan segmen garis yang beralih dari titik C ke titik tengah D, yang terletak di sisi yang berlawanan (AB). Segmen ini berukuran 62 meter. Hitung luas dan perimeter segitiga sama sisi itu.

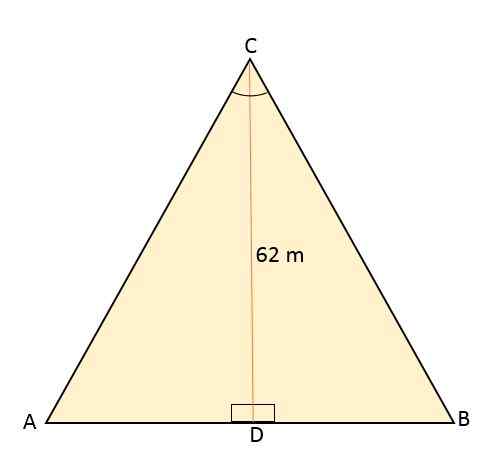
Larutan

Mengetahui bahwa segitiga sama sisi dibagi dengan segmen garis yang sesuai dengan ketinggian, sehingga membentuk dua persegi panjang kongruen, ini pada gilirannya juga membagi sudut Vertex C menjadi dua sudut dengan ukuran yang sama, 30^{salah satu} setiap.

Tingginya membentuk sudut 90^{salah satu} Sehubungan dengan segmen AB, dan sudut simpul untuk kemudian mengukur 60^{salah satu}.

Kemudian menggunakan sudut 30 sebagai referensi^{salah satu}, Tinggi CD ditetapkan sebagai cateto yang berdekatan dengan sudut dan BC sebagai hipotenusa.

Dari data ini, nilai salah satu sisi segitiga dapat ditentukan, menggunakan alasan trigonometri:

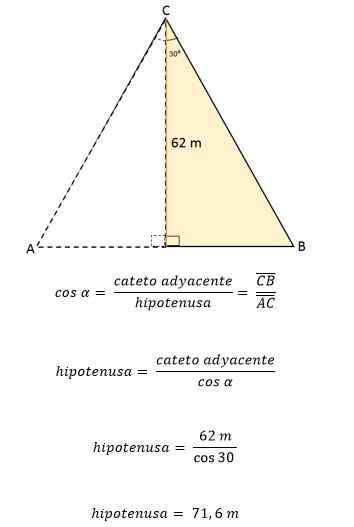
Seperti pada segitiga sama sisi, semua sisi memiliki ukuran atau panjang yang persis sama, itu berarti bahwa setiap sisi segitiga sisi ABC sama dengan 71,6 meter. Mengetahui hal itu, adalah mungkin untuk menentukan area Anda:

Area = b * h ÷ 2

Area = (71,6 m _* 62 m) ÷ 2

Area = 4.438.6 m² ÷ 2

Area = 2.219,3 m²

Perimeter diberikan dengan jumlah dari ketiga sisinya:

P = sisi + sisi + sisi = 3 _* l

P = 3_*l

P = 3 _* 71,6 m

P = 214.8 m.

Referensi

1. Álvaro rendón, ke. R. (2004). Gambar Teknis: Buku catatan aktivitas.
2. Arthur Goodman, L. H. ( seribu sembilan ratus sembilan puluh enam). Aljabar dan trigonometri dengan geometri analitik. Pendidikan Pearson.
3. Baldor, a. (1941). Aljabar. Havana: Budaya.
4. Barbosa, J. L. (2006). Geometri Euclidean datar. SBM. Rio de Janeiro, .
5. Coxford, a. (1971). Geometri pendekatan transformasi. AS: Laidlaw Brothers.
6. Euclid, r. P. (1886). Elemen geometri Euclid.
7. Héctor Trejo, J. S. (2006). Geometri dan Trigonometri.
8. León Fernández, G. S. (2007). Geometri terintegrasi. Lembaga Teknologi Metropolitan.
9. Sullivan, J. (2006). Aljabar dan Trigonometri. Pendidikan Pearson.