Tetradecágono

Apa itu tetradecágono?

Tetradecágono adalah sosok geometris yang datar dan tertutup dari 14 sisi, milik keluarga poligon. Itu juga dikenal dengan nama Tetrakaidecágono, Semua kata yang berasal dari kata -kata Yunani: "tetra" (cuatri), "kai" (lebih), "peluruhan" (sepuluh) dan "gon" (sudut), karena juga memiliki 14 sudut interior.

Gambar tersebut menunjukkan tetradagon biasa, yaitu, yang sisi dan sudut internal semuanya memiliki ukuran yang sama, menunjukkan karakteristik utama dari gambar ini.

Gambar 1.- Tetrade biasa dengan karakteristik utamanya. Sumber: f. Zapata.

Elemen Tetradecágono

• Sisi: Mereka disebut segmen 14 garis yang tertutup untuk membentuk gambar. Mereka semua dapat memiliki panjang yang sama, dalam hal ini poligon teratur, atau mereka bisa berbeda dan kemudian ada tetrade yang tidak teratur.
• Sudut: Mereka adalah titik persimpangan antara segmen berturut -turut dan tetradecágono memiliki 14 simpul.
• Tengah: Titik sama dari simpul.
• Radio: segmen yang menyatukan pusat dengan titik.
• Sudut internal: Ini dibentuk oleh bagian dalam sosok dan antara dua segmen berturut -turut atau berdekatan. Ukuran 154.286º untuk tetradecágon biasa, terlepas dari ukuran sisinya.
• Sudut eksternal: terbentuk di antara satu sisi dan perpanjangan salah satu sisi yang berdekatan. Terlepas dari panjang sampingnya, sudut ini berukuran 25.7143º untuk tetrade biasa.
• Sudut tengah: Orang yang memiliki simpulnya bertepatan dengan pusat poligon dan sisinya adalah dua radio berturut -turut.
• Diagonal: segmen yang menghubungkan dua simpul non -berturut -turut.

Bagaimana tetradecágono?

Poligon reguler dari sisi N yang dibangun dengan aturan dan kompas memiliki n dari bentuk 2^R P₁… P_k, menjadi p_yo Fermat primo bilangan berbeda, dan pada gilirannya bilangan prima Fermat berbentuk 2^N + 1.

Dapat melayani Anda: menunggu garis: formula dan persamaan, representasi, contoh

Tetradecágono memiliki n = 14 sisi, tetapi 14 = 7 × 2, yang bukan sepupu Fermat, karena mereka tidak dapat diekspresikan dengan cara yang ditunjukkan. Oleh karena itu poligon ini tidak mengakui konstruksi yang tepat dengan aturan dan kompas, tetapi konstruksi yang mendekati dengan sangat baik, melalui beberapa metode.

Metode umum untuk membangun poligon biasa

Berikut ini adalah metode umum (bukan satu -satunya) untuk membangun poligon biasa yang terdaftar di lingkar, termasuk tetrade biasa.

Ini terdiri dari membagi diameter vertikal dari lingkar ini menjadi sebanyak mungkin bagian yang sama dengan sisi memiliki poligon untuk menggambar. Dalam kasus tetradecágono mereka akan menjadi 14 bagian yang diberi nomor dalam gambar 2. Ini adalah langkah -langkahnya:

• Gambarlah diameter vertikal dari A ke B.
• Kemudian gambar semi -benar mulai dari titik A, buka kompas dengan pembukaan sewenang -wenang dan buat 14 divisi yang sama -sama berjarak. Semirrect dan pembagiannya bisa keluar dari lingkar.
• Bergabunglah dengan merek 14VA (dengan warna biru dalam gambar) di akhir semi -benar dengan titik B.
• Untuk terus bergabung dengan sisa tanda di semi -recreational dengan titik masing -masing pada diameter vertikal (titik hijau).
• Dengan ujung kompas dalam a dan pembukaan sama dengan ukuran diameter keliling sebuah busur ditarik. Dengan ukuran yang sama, tetapi mendukung ujung dalam B (titik 14 dari Gambar 2) lengkungan lain ditarik, yang dipotong dengan yang pertama pada titik V dan V 'ditunjukkan.

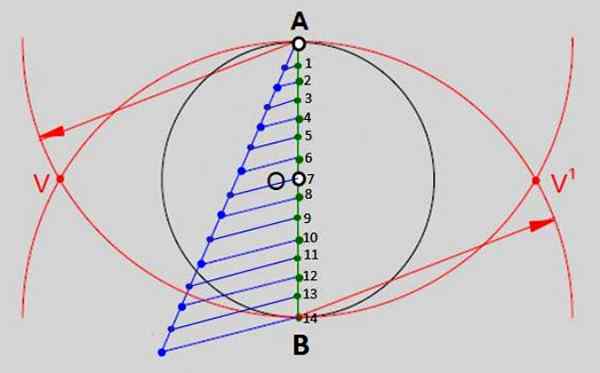Gambar 2.- Salah satu metode umum untuk membangun poligon reguler adalah membagi diameter keliling menjadi bagian yang sama dengan yang sama memiliki poligon. Dalam kasus tetradech biasa, ada 14 bagian yang sama. Sumber: f. Zapata.

• Sekarang, dengan aturan, gambar garis dari V 'ke titik 2 dan memperpanjangnya untuk memotong keliling pada titik C pada Gambar 3. Tandai titik persimpangan, yang akan menjadi salah satu simpul sosok.

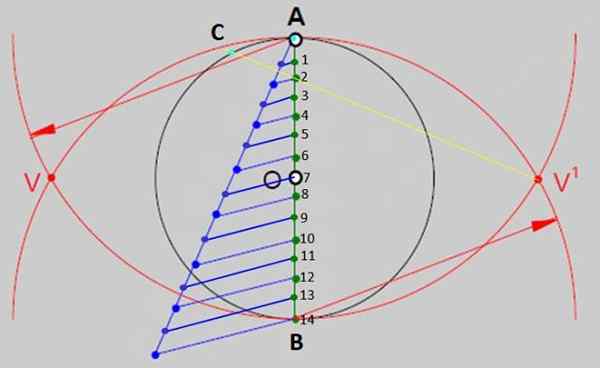Dapat melayani Anda: cabang statistik Gambar 3.- Segmen AC adalah ukuran sisi tetradecion yang dibangun. Sumber: f. Zapata.

• Buka kompas dalam jarak AC dan mendukung ujung dalam A atau C, menggambar lengkungan dengan ukuran yang sama di seluruh lingkar, dengan cara ini dibagi menjadi bagian yang kira -kira sama, persimpangan antara lengkungan dan keliling adalah simpul adalah simpul simpul tetradecágono.
• Dengan aturan, bergabunglah dengan simpul dengan segmen garis, membentuk sisi poligon.
• Hapus konstruksi tambahan dengan hati -hati.

Dalam animasi berikut, metode perkiraan lain ditampilkan, dengan aturan dan kompas:

Gambar 4.- Animasi yang menunjukkan bagaimana tetradecágon dibuat (kira -kira poligon biasa). Sumber: Wikimedia Commons.

Rumus untuk tetrade biasa

Rumus berikut ini berlaku untuk poligon biasa:

• Nomor Lembar: N
• Ukuran samping: a
• Apothem: l_KE
• Radio: r
• Perimeter: p
• Area: a
• Sudut internal: i
• Sudut Eksternal: E
• Diagonal: d

Sisi Apothem Dikenal

A = 2l_KE × tg (π/n)

Untuk n = 14:

A = 2l_KE × TG (π/14)

Sisi yang Dikenal Radio

A = 2r × sen (π/n)

Ya n = 14:

A = 2R × Sen (π/14)

Di sekeliling sisi yang dikenal

Perimeter adalah jumlah sisi. Ketika Tetradecágono biasa:

P = n⋅a = 14⋅a

Jika tetradecágono tidak teratur, semua sisi harus ditambahkan langsung untuk mendapatkan perimeter.

Area yang Dikenal Sisi

A = ¼ na² × cot (π/n)

Untuk n = 14:

A = ¼ (14th²) × cot (π/14) = (7/2) a² × cot (π/14)

Area yang dikenal

A = N⋅L_KE ² × tg (π/n)

Mengambil N = 14 Hasil:

A = 14L_KE ² × TG (π/14)

Area berdasarkan perimeter dan apothem

A = (p × l_KE)/2

Dapat melayani Anda: Teorema Bayes

Ukuran sudut dalam

 Ketika n = 14, sudut internal tetradecágono berukuran dalam derajat:

I = 12 × 180º /14 = 154.286º

Pengukuran sudut eksternal

E = 360º/n

Ketika n = 14 Anda memiliki:

E = 25.7143º

Diagonal

Rumus untuk menghitung jumlah diagonal yang ada dalam poligon apa pun, biasa atau tidak, adalah:

Untuk n = 14:

D = 14 × 11/2 = 77 Diagonals

Contoh

Contoh lain dari Tetradecágon

Poligon biasa muncul berulang kali dalam berbagai desain, seperti mata uang. Dalam kasus tetradagon biasa, ini muncul dalam koin peringatan Malaysia, mewakili sisi -sisinya untuk masing -masing dari empat belas negara bagian Konfederasi negara itu.

Cekung dan cembung tetradecágonos

Secara umum, poligon seperti tetradecágono dapat menjadi cembung atau cekung, dalam kasus pertama, ukuran sudut internal mereka tidak melebihi 180º. Tetradech biasa adalah cembung, seperti poligon biasa, karena sudut internalnya berukuran 154.286º.

Di sisi lain, di tetradech cekung, satu atau lebih sudut internalnya berukuran lebih dari 180º.

Contoh numerik

Diberikan tetradagon biasa yang sampingannya berukuran 5 cm, temukan:

a) Perimeter
b) pengukuran apothem
c) Panjang radio
d) area

Jawaban

a) Karena itu adalah poligon biasa, perimeternya adalah:

P = 14 × 5 cm = 70 cm.

b) Dari Persamaan A = 2L_KE × tg (π/14), di mana a = 5 cm, apothem l_KE:

L_KE = A / [2 × TG (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

C) Radio R dapat dihitung dengan A = 2R × Sen (π/14):

R = a / [2 × dosa (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Ada beberapa alternatif untuk area tersebut, misalnya a = (p × l_KE)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Geometri Arturo. Metode Umum untuk Menggambar Poligon Yang Terdaftar di Lingkar. Pulih dari youtube.com
3. Kalkulator sup. Kalkulator poligon biasa. Dipulihkan dari: calculatorOup.com.
4. Menggambar. Poligon biasa. Pulih dari: menggambar.com.
5. Requena, b. Poligon cekung. Pulih dari: universoformulas.com.
6. Wikipedia. Poligon yang dapat dibangun. Pulih dari: is.Wikipedia.org.