Jenis integral
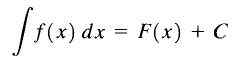
- 3882
- 1216
- Leland Robel
Itu Jenis integral bahwa kita berada dalam perhitungan adalah integral yang tidak terbatas dan integral yang ditentukan. Meskipun integral yang didefinisikan memiliki lebih banyak aplikasi daripada integral yang tidak terbatas, pertama -tama perlu untuk belajar menyelesaikan integral yang tidak terbatas.
Salah satu aplikasi paling menarik dari integral yang ditentukan adalah perhitungan volume revolusi yang padat. Kedua jenis integral memiliki sifat linieritas yang sama dan juga teknik integrasi tidak tergantung pada jenis integral.
Tetapi meskipun sangat mirip, ada perbedaan utama; Dalam tipe integral pertama hasilnya adalah fungsi (yang tidak spesifik) sedangkan pada tipe kedua hasilnya adalah angka.
Jenis dasar integral
Dunia integral sangat luas, tetapi dalam hal ini kita dapat membedakan dua jenis dasar integral, yang memiliki penerapan yang hebat dalam kehidupan sehari -hari.
1- Integral yang tidak terbatas
Jika f '(x) = f (x) untuk semua x dalam domain f, kami mengatakan bahwa f (x) adalah antiderivatif, primitif atau integral f (x).
Di sisi lain, mari kita perhatikan bahwa (f (x)+c) '= f' (x) = f (x), yang menyiratkan bahwa integral fungsi tidak unik, karena memberikan nilai yang berbeda pada konstanta C Kami akan mendapatkan antiderivatif yang berbeda.
Untuk alasan ini f (x)+C disebut integral tak terbatas dari f (x) dan c disebut konstan integrasi dan kami menulisnya sebagai berikut:
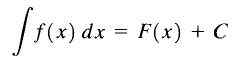 Integral yang tidak terbatas
Integral yang tidak terbatas Seperti yang bisa kita lihat, integral yang tidak terbatas dari fungsi f (x) adalah keluarga fungsi.
Misalnya, jika Anda ingin menghitung integral yang tidak terbatas dari fungsi f (x) = 3x², pertama antiderivatif f (x) harus ditemukan terlebih dahulu.
Dapat melayani Anda: trinomialMudah dicatat bahwa f (x) = x³ adalah antiderivatif, karena f '(x) = 3x². Oleh karena itu, dapat disimpulkan itu
∫f (x) dx = ∫3x²dx = x³+c.
2- integral yang didefinisikan
Misalkan y = f (x) fungsi nyata berlanjut dalam interval tertutup [a, b] dan menjadi f (x) antiderivatif f (x). Ini disebut integral yang ditentukan dari f (x) antara batas A dan B ke angka f (b) -f (a), dan menunjukkan sebagai berikut:
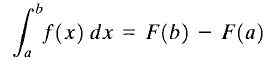 Teorema Perhitungan Dasar
Teorema Perhitungan Dasar Rumus yang ditunjukkan di atas lebih dikenal sebagai "Teorema Fundamental Perhitungan". Di sini "A" disebut batas bawah dan "B" disebut batas atas. Seperti yang dapat dilihat, integral yang pasti dari suatu fungsi adalah angka.
Dalam hal ini, jika integral yang ditentukan dari F (x) = 3x² dihitung dalam interval [0,3], angka akan diperoleh.
Untuk menentukan nomor ini kita memilih f (x) = x³ sebagai antiderivatif f (x) = 3x². Kemudian, kami menghitung f (3) -f (0) yang melempar kami sebagai hasilnya 27-0 = 27. Kesimpulannya, integral yang didefinisikan dari f (x) dalam interval [0,3] adalah 27.
Dapat dicatat bahwa jika g (x) = x³+3, maka g (x) dipilih, adalah antiderivatif f (x) berbeda dari f (x), tetapi ini tidak mempengaruhi hasilnya sebagai g (3) -g (0) = (27+3)-(3) = 27. Untuk alasan ini, dalam integral yang ditentukan, konstanta integrasi tidak muncul.
Salah satu aplikasi paling berguna yang dimiliki jenis integral ini adalah memungkinkan untuk menghitung area (volume) dari figur datar (dari revolusi yang solid), membangun fungsi dan batas integrasi yang memadai (dan sumbu rotasi).
Di antara integral yang didefinisikan, kita dapat menemukan berbagai ekstensi yang satu ini seperti garis integral, integral permukaan, integral yang tidak tepat, integral berganda, antara lain, semua dengan aplikasi yang sangat berguna dalam sains dan teknik.
Itu dapat melayani Anda: perbedaan antara lingkaran dan keliling (dengan contoh)Referensi
- Kishan, h. (2005). Kalkulus integral. Penerbit & Distributor Atlantik.
- Purcell, e. J., VARBERG, D., & Rigdon, s. DAN. (2007). Perhitungan (Edisi kesembilan.). Prentice Hall.

