Fitur pemotretan horizontal, formula dan persamaan, latihan

Dia Penembakan horizontal Ini adalah peluncuran proyektil dengan kecepatan horizontal dari ketinggian tertentu dan dibiarkan aksi gravitasi. Tanpa memperhitungkan resistensi udara, lintasan yang dijelaskan oleh ponsel akan memiliki bentuk busur parabola.

Proyeksi objek secara horizontal cukup umum. Proyektil dilemparkan dengan segala macam tujuan: dari batu -batu yang dengannya bendungan itu sedih di awal cerita, hingga yang dilakukan dalam olahraga bola dan diikuti oleh orang banyak.

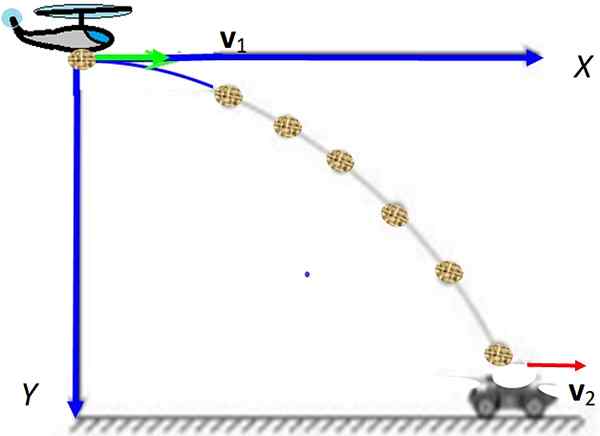
Gambar 1. Pemotretan horizontal dengan komponen kecepatan merah. Perhatikan bahwa komponen horizontal tetap konstan saat vertikal tumbuh. Sumber: Wikimedia Commons.

[TOC]

Karakteristik

Karakteristik utama pemotretan horizontal adalah:

-Kecepatan awal yang disediakan untuk proyektil tegak lurus terhadap gravitasi.

-Gerakan ini terjadi di pesawat, jadi dua koordinat diperlukan: X Dan Dan.

-Itu dilakukan dari ketinggian tertentu h di atas permukaan tanah.

-Waktu proyektil berlangsung di udara dipanggil waktu penerbangan.

-Faktor -faktor seperti resistensi udara atau fluktuasi tidak diperhitungkan dalam nilai G.

-Bentuk, ukuran, dan massa proyektil tidak mempengaruhi pergerakannya.

-Gerakan ini terurai menjadi dua gerakan simultan: satu vertikal di bawah aksi G; Yang lain, horizontal, dengan kecepatan konstan.

Rumus dan Persamaan

Persamaan sinematik untuk peluncuran horizontal diperoleh dari persamaan untuk jatuh bebas dan gerakan seragam bujursangkar yang seragam.

Dapat melayani Anda: energi internal

Seperti yang ditunjukkan oleh animasi pada Gambar 1, proyektil ini dilengkapi dengan kecepatan awal horizontal, dilambangkan sebagai v_{salah satu} = v_sapi yo (Teks cetak tebal menunjukkan bahwa itu adalah vektor).

Perlu dicatat bahwa kecepatan awal memiliki besarnya v_sapi dan diarahkan di sepanjang poros X, Apa arah vektor unit yo. Dalam animasi itu juga diperingatkan bahwa kecepatan awal tidak memiliki komponen vertikal, tetapi saat jatuh, komponen ini meningkat secara seragam, berkat aksi G, percepatan gravitasi.

Adapun komponen kecepatan horizontal, tetap konstan saat gerakan berlangsung.

Menurut apa yang telah dikatakan, posisi ditetapkan sebagai fungsi waktu, baik pada sumbu horizontal dan pada sumbu vertikal. Hak diambil sebagai +x sumbu, sedangkan turun adalah alamat -dan. Nilai gravitasi adalah G = -9.8 m/s² salah satu -32 kaki/s²:

x (t) = x_{salah satu} + v_sapi.t (posisi horizontal); v_sapi itu konstan

dan (t) = y_{salah satu} + v_Oy.T - ½ g.T² (posisi vertikal); v_Dan = v_Oy - G.T (kecepatan vertikal)

Posisi, Kecepatan, Waktu Penerbangan dan Kisaran Horizontal Maksimal

Persamaan disederhanakan jika mereka memilih posisi awal berikut: X_{salah satu} = 0, Dan_{salah satu} = 0 di tempat peluncuran. Di samping itu v_Oy = 0, karena ponsel diproyeksikan secara horizontal. Dengan pilihan ini, persamaan gerakan seperti ini:

x (t) = v_sapi.T; v_X = v_sapi

dan (t) = - ½ g.T²; v_Dan = - g.T

Ketika waktu tidak tersedia, persamaan yang menghubungkan kecepatan dan perpindahan bermanfaat. Ini berlaku untuk kecepatan vertikal, karena horizontal tetap konstan di seluruh gerakan:

Dapat melayani Anda: kalsium fluoride (caf2): struktur, sifat, penggunaan

v_Dan² = v_Oy² + 2.G .y = 2.G.Dan

Waktu penerbangan

Untuk menghitung Waktu penerbangan t_penerbangan, Misalkan ponsel diproyeksikan dari ketinggian H di lantai. Karena asal sistem referensi pada titik peluncuran telah dipilih, ketika mencapai tanah di posisinya -H. Mengganti ini dalam persamaan 2) diperoleh:

-H = - ½ g.T²_penerbangan

T_penerbangan = (2H/g)^½

Kisaran maksimum

Dia Jangkauan horizontal Kali ini diperoleh dengan mengganti x (t):

X_Max = v_sapi. (2H/g)^½

Latihan terpecahkan

-Latihan diselesaikan 1

Helikopter terbang secara horizontal, mempertahankan ketinggian konstan 580 m saat melepaskan sebuah kotak yang berisi makanan di kamp pengungsi. Kotak itu mendarat pada jarak horizontal 150 m dari titik peluncurannya. Temukan: a) Waktu penerbangan kotak.

b) kecepatan helikopter.

c) Seberapa cepat kotak disentuh?

Larutan

a) Tinggi h dari mana makanan dilepaskan adalah h = 500 m. Dengan data ini saat mengganti Anda mendapatkan:

T_penerbangan = (2H/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) Helikopter membawa kecepatan awal horizontal v_sapi paket dan karena salah satu data X_Max:

X_Max = v_sapi. (2H/g)^½ ® v_sapi = x_Max /(2H/g)^½= x_Max / T_penerbangan = 150 m/ 10.9 s = 13.8 m/s

c) Kecepatan proyektil kapan saja adalah:

v_Dan = -g.T = -9.8 m/ s² x 10.9 s = -106.82 m/s = - 384.6 km/jam

Tanda negatif menunjukkan bahwa ponsel bergerak ke bawah.

-Latihan diselesaikan 2

Dari pesawat yang terbang secara horizontal pada ketinggian H = 500 m Dan 200 km/jam Paket jatuh yang harus jatuh pada kendaraan terbuka yang berbaris 18 km/jam di jalan. Di posisi mana pesawat harus membiarkan paket jatuh ke dalam kendaraan? Jangan memperhitungkan ketahanan udara atau kecepatan angin.

Dapat melayani Anda: analisis dimensiGambar 2. Skema untuk latihan diselesaikan 2. Sumber: disiapkan oleh f. Zapata.

Larutan

Lebih mudah untuk terlebih dahulu meneruskan semua unit ke sistem internasional:

18 km/jam = 6 m/s

200 km /jam = 55 m /s

Ada dua ponsel: pesawat (1) dan kendaraan (2) dan perlu untuk memilih sistem koordinat untuk menemukan keduanya. Lebih mudah untuk melakukannya di titik awal paket di pesawat. Paket ini diproyeksikan secara horizontal dengan kecepatan yang dibawa oleh pesawat: v₁, Saat kendaraan bergerak ke v₂ seharusnya konstan.

-Pesawat

Posisi awal: x = 0; y = 0

Kecepatan awal = v₁ (horisontal)

Persamaan posisi: dan (t) = -½g.T²  ; x (t) = v₁.T

-Kendaraan

Posisi awal: x = 0, y = -h

Kecepatan awal = v₂  (konstan)

x (t) = x_{salah satu} + v₂. T

Waktu penerbangan paket berlangsung adalah:

T_penerbangan = (2H/g)^½ = (2 × 500/9.8)^½S = 10.1 s

Pada saat ini, paket tersebut telah mengalami perpindahan horizontal dari:

X_Max = v_sapi . (2H/g)^½= 55 m/s x 10.1 s = 556 m.

Pada saat ini, kendaraan juga bergerak secara horizontal:

x (t) = v₁.T = 6 m/s x10.1 s = 60.6 m

Jika pesawat segera melepaskan paket bahwa kendaraan melihat transit di bawahnya, itu tidak akan bisa jatuh langsung ke dalamnya. Agar hal itu terjadi, dia harus membuangnya ke belakang:

D = 556 m - 60.6 m = 495.4 m.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 74-84.
2. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).117 - 164.
3. Gerak Proyektil. Pulih dari: Phys.Librettexts.org.
4. Rex, a. 2011. Dasar -dasar fisika. Pearson. 53-58.
5. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit McGraw. 126-131.