Karakteristik tembakan parabola oblicual, formula, persamaan, contoh

Dia Tembakan parabola oblicual Ini adalah kasus khusus dari gerakan jatuh bebas di mana kecepatan awal proyektil membentuk sudut tertentu dengan horizontal, menghasilkan jalur parabola.

Jatuh bebas adalah kasus gerakan dengan akselerasi konstan, di mana akselerasi adalah gravitasi, yang selalu mengarah ke bawah secara vertikal dan memiliki besarnya 9,8 m/s^2. Itu tidak tergantung pada adonan proyektil, seperti yang ditunjukkan Galileo Galilei pada 1604.

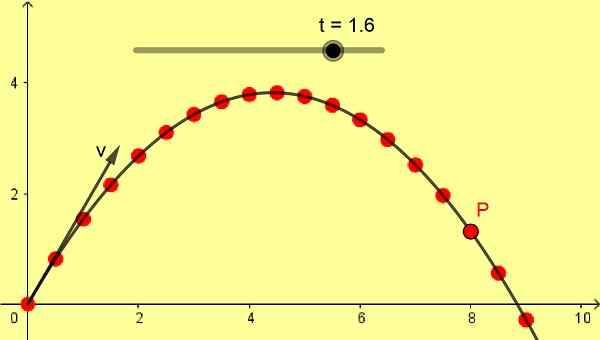Gambar 1. Tembakan parabola oblicual. (Elaborasi sendiri)

Jika kecepatan proyektil awal vertikal, jatuh bebas memiliki lintasan lurus dan vertikal, tetapi jika kecepatan awal maka miring lintasan jatuh bebas adalah kurva parabola, juga ditunjukkan oleh Galileo.

Contoh gerakan parabola adalah lintasan yang mengikuti bisbol, peluru yang ditembakkan oleh meriam dan jet air yang keluar dari selang.

Gambar 1 menunjukkan bidikan parabola miring 10 m/s dengan sudut 60º. Skala dalam meter dan posisi P berturut -turut diambil dengan perbedaan 0,1 detik mulai dari momen awal 0 detik.

[TOC]

Rumus

Pergerakan partikel sepenuhnya dijelaskan jika posisinya diketahui, kecepatannya dan akselerasinya sebagai fungsi waktu.

Gerakan parabola yang dihasilkan dari tembakan miring adalah superposisi gerakan horizontal pada kecepatan konstan, ditambah gerakan vertikal dengan akselerasi konstan sama dengan percepatan gravitasi.

Rumus yang berlaku untuk tembakan parabola miring adalah yang sesuai dengan gerakan dengan akselerasi konstan a = g, Perhatikan bahwa tebal telah digunakan untuk menunjukkan bahwa akselerasi adalah jumlah vektor.

Dapat melayani Anda: satelit alami

Posisi dan kecepatan 

Dalam gerakan akselerasi yang konstan, posisi secara matematis tergantung pada waktu dengan cara kuadratik.

Jika kita menunjukkan R(T) Posisi waktu T, Rsalah satu Posisi instan awal, vsalah satu Kecepatan awal, G percepatan dan t = 0 sebagai momen awal formula yang memberikan posisi untuk setiap momen waktu T adalah:

R(t) = R_{salah satu} + v_{salah satu} T + ½ G T²

Tebal dalam ekspresi sebelumnya menunjukkan bahwa itu adalah persamaan vektor.

Kecepatan sebagai fungsi waktu diperoleh dari mengambil turunan sehubungan dengan t posisi dan hasilnya adalah:

v(t) = v_{salah satu} + G T

Dan untuk mendapatkan akselerasi sebagai fungsi waktu, kecepatan berasal dari T yang dihasilkan:

ke(t) = G

Ketika waktu tidak tersedia, ada hubungan antara kecepatan dan posisi, yang diberikan oleh:

v² = vsalah satu² - 2 g (dan - saya)

Persamaan

Selanjutnya kita akan menemukan persamaan yang berlaku untuk tembakan parabola miring dalam bentuk Cartesian.

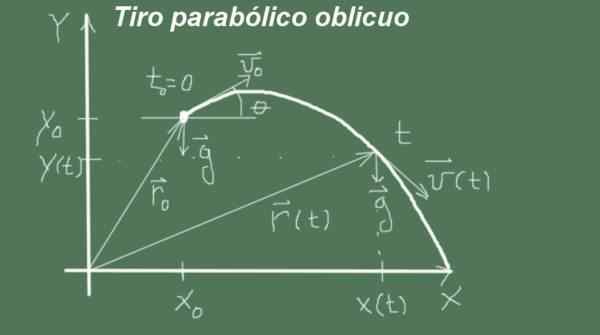
Gambar 2. Variabel dan parameter tembakan parabola miring. (Elaborasi sendiri)

Gerakan dimulai saat ini t = 0 Dengan posisi awal (Xo, saya) dan kecepatan besarnya vsalah satu dan sudut θ, artinya vektor kecepatan awal (vsalah satu cosθ, vsalah satu senθ). Gerakan berlalu dengan akselerasi 

G = (0, -g).

Persamaan Parametrik

Jika rumus vektor yang memberikan posisi sebagai fungsi waktu diterapkan dan komponen dikelompokkan dan disamakan, persamaan yang diberikan oleh koordinat posisi untuk setiap saat waktu t akan diperoleh.

x (t) = x_{salah satu} + v_sapi T 

dan (t) = y_{salah satu} + v_Oy t -½ g t²

Demikian pula, persamaan dimiliki untuk komponen kecepatan sebagai fungsi waktu.

Itu dapat melayani Anda: upaya normal: apa yang terdiri dari, bagaimana itu dihitung, contoh

v_X(t) = v_sapi

v_Dan(t) = v_Oy - g t 

Di mana: v_sapi = vsalah satu cosθ; v_Oy = vsalah satu Senθ

Persamaan lintasan

y = a x^2 + b x + c

A = -g/(2 Vsapi^2)

B = (vOy/vsapi + g xsalah satu/vsapi^2)

C = (dansalah satu - vOy Xsalah satu / vsapi)

Contoh 

Contoh 1

Jawab pertanyaan berikut:

a) Mengapa dalam masalah penembakan parabola biasanya membenci efek gesekan dengan udara?

b) Apakah bentuk objek dalam bidikan parabola?

Jawaban

a) Agar pergerakan proyektil menjadi parabola, penting bahwa gaya gesekan udara jauh lebih rendah daripada bobot objek yang diluncurkan. 

Jika bola gabus atau bahan cahaya dilemparkan, gaya gesekan sebanding dengan berat dan lintasannya tidak dapat mendekati parabola.

Sebaliknya, jika itu adalah benda berat seperti batu, gaya gesekan dapat diabaikan dibandingkan dengan berat batu dan lintasannya dekat dengan parabola.

b) bentuk objek yang diluncurkan juga relevan. Jika plata bidang dalam bentuk avionncito diluncurkan, pergerakannya tidak akan bebas atau parabola, karena bentuknya mendukung ketahanan udara.

Di sisi lain, jika lembar kertas yang sama kompak dalam bentuk bola, gerakan yang dihasilkan sangat mirip dengan parabola.

Contoh 2

Proyektil diluncurkan dari lantai horizontal dengan cepat 10 m/s dan 60º sudut. Ini adalah data yang sama dengan yang dikembangkan Gambar 1. Dengan data ini saya temukan:

a) momen di mana ia mencapai ketinggian maksimum.

Dapat melayani Anda: apa sifat termal dan apa itu? (Dengan contoh)

b) Tinggi maksimum.

c) kecepatan pada ketinggian maksimum.

d) Posisi dan kecepatan pada 1,6 detik.

e) Saat dia bermain tanah lagi.

f) Lingkup horizontal.

Solusi untuk)

Kecepatan vertikal tergantung pada waktunya

v_Dan(t) = v_Oy - G t = v_{salah satu} Senθ - G T = 10 sen60º - 9.8 t = 8.66 - 9.8 t 

Pada saat ketinggian maksimum tercapai, kecepatan vertikal adalah nol untuk instan.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Solusi b)

Tinggi maksimum diberikan oleh koordinat Dan Untuk saat di mana ketinggian itu tercapai:

dan (0.88S) = Yo saya akan t --½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Oleh karena itu ketinggian maksimum adalah 3.83 m.

Solusi C)

Kecepatan pada ketinggian maksimum horizontal:

v_X(t) = v_sapi = v_{salah satu} cosθ = 10 cos60º = 5 m/s 

D) Solusi

Posisi di 1.6 s adalah:

X (1.6) = 5*1.6 = 8.0 m

dan 1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m

Solusi e)

Ketika koordinat menyentuh dan dibatalkan, lalu:

dan (t) = 8.66*t --½ 9.8 t2 = 0 ⇒ t = 1,77 s

Solusi f)

Lingkup horizontal adalah koordinat x tepat pada saat yang memainkan tanah:

X (1.77) = 5*1.77 = 8.85 m

Contoh 3

Temukan persamaan lintasan dengan Contoh 2 Data.

Larutan 

Persamaan parametrik lintasan adalah:

x (t) = 5*t

dan (t) = 8.66*t --½ 9.8 t^2

Dan persamaan Cartesian diperoleh dengan membersihkan t yang pertama dan mengganti di yang kedua

y = 8.66*(x/5) --½ 9.8 (x/5)^2

Menyederhanakan:

y = 1,73 x - 0,20 x^2 

Referensi

1. P. P. Teodorescu (2007). "Kinematics". Sistem Mekanik, Model Klasik: Mekanika Partikel. Peloncat.
2. Resnick, Halliday & Krane (2002). Volume Fisika 1. CECSA, Meksiko.
3. Thomas Wallace Wright (1896). Elemen mekanik termasuk kinematika, kinetika dan statika. E dan fn spon.
4. Wikipedia. Gerakan parabola. Pulih dari es.Wikipedia.org.
5. Wikipedia. Gerak Proyektil.Diterima dari.Wikipedia.org.