Transformasi isometrik

Itu Transformasi isometrik Mereka adalah perubahan posisi atau orientasi dari gambar tertentu yang tidak mengubah bentuk atau ukurannya. Transformasi ini diklasifikasikan menjadi tiga jenis: terjemahan, rotasi dan refleksi (isometri). Secara umum, transformasi geometris memungkinkan untuk membuat angka baru dari yang diberikan lainnya.

Transformasi menjadi sosok geometris berarti bahwa, dalam beberapa hal, itu mengalami beberapa perubahan; Artinya, itu diubah. Menurut rasa aslinya dan serupa di bidang, transformasi geometris dapat diklasifikasikan menjadi tiga jenis: isometrik, isomorfik dan anamorfik.

Karakteristik transformasi isometrik

- Transformasi isometrik terjadi ketika besaran segmen dan sudut antara sosok asli dan sosok yang diubah dipertahankan.

- Dalam jenis transformasi ini, bentuk atau ukuran gambar tidak diubah (mereka kongruen), itu hanya perubahan posisi ini, baik dalam orientasi atau dalam arti. Dengan cara ini, angka awal dan final akan serupa dan secara geometris kongruen.

- Isometri mengacu pada kesetaraan; yaitu, angka geometris itu akan menjadi isometrik jika mereka memiliki bentuk dan ukuran yang sama.

- Dalam transformasi isometrik, satu -satunya hal yang dapat diamati adalah perubahan posisi di pesawat, gerakan kaku terjadi berkat sosok yang ditularkan dari posisi awal ke final. Angka ini disebut homolog (serupa) dari yang asli.

- Ada tiga jenis gerakan yang mengklasifikasikan transformasi isometrik: terjemahan, rotasi dan refleksi atau simetri.

Jenis transformasi isometrik

Dengan terjemahan

Adalah isometri yang memungkinkan untuk menggusur dalam garis lurus semua titik pesawat dalam arah dan jarak tertentu.

Ketika suatu gambar diubah oleh terjemahan, ia tidak mengubah orientasinya dalam kaitannya dengan posisi awal, juga tidak kehilangan langkah -langkah internalnya, ukuran sudut dan sampingnya. Jenis perpindahan ini ditentukan oleh tiga parameter:

• Alamat, yang bisa horizontal, vertikal atau miring.
• Arah, yang bisa ke kiri, kanan, ke atas atau ke bawah.
• Jarak atau besarnya, yang merupakan panjang yang berasal dari posisi awal ke final dari setiap titik yang bergerak.

Dapat melayani Anda: Curtosis: Definisi, Jenis, Rumus, untuk apa, misalnya

Agar transformasi isometrik karena terjemahan, ia harus memenuhi kondisi berikut:

• Sosok harus selalu menyimpan semua dimensinya, baik linier maupun sudut.
• Gambar tersebut tidak mengubah posisinya sehubungan dengan sumbu horizontal; yaitu, sudutnya tidak pernah bervariasi.
• Terjemahan akan selalu dirangkum dalam satu, terlepas dari jumlah terjemahan yang dibuat.

Di bidang di mana pusat adalah titik atau, dengan koordinat (0,0), terjemahan ditentukan oleh vektor t (a, b), yang menunjukkan perpindahan titik awal. Artinya:

P (x, y) + t (a, b) = p '(x + a, y + b)

Misalnya, jika ke titik koordinat p (8, -2) terjemahan t (-4, 7) diterapkan, diperoleh:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

Pada gambar berikut (kiri) Anda dapat melihat bagaimana titik C bergerak bertepatan dengan D. Dia melakukannya secara vertikal, artinya naik dan jarak atau magnitude CD adalah 8 meter. Di gambar kanan terjemahan segitiga diamati:

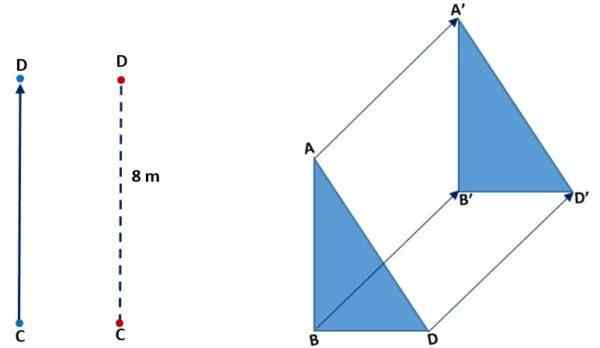
Dengan rotasi

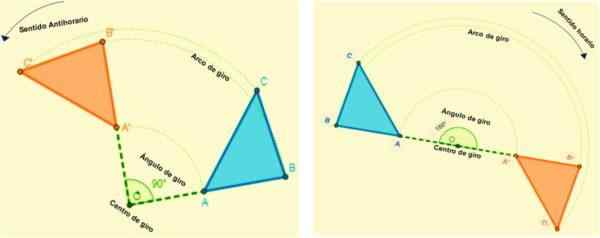
Adalah isometri yang memungkinkan sosok itu mengubah semua titik pesawat. Setiap titik berputar mengikuti busur yang memiliki sudut konstan dan titik tetap (pusat belok) ditentukan.

Artinya, semua rotasi akan ditentukan oleh rotasi dan pusat sudut beloknya. Saat sosok ditransformasikan oleh rotasi, ia mempertahankan ukuran sudut dan sampingnya.

Rotasi terjadi pada arah tertentu, positif ketika belokan anti -horary (bertentangan dengan bagaimana tangan jam berputar) dan negatif ketika belokannya dalam arah searah jarum jam.

Jika titik (x, y) diputar sehubungan dengan asal -yaitu, pusat rotasinya adalah (0,0) -, pada sudut 90^{salah satu} 360^{salah satu} Koordinat poin adalah:

Dapat melayani Anda: cabang statistik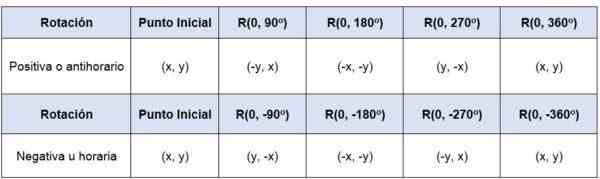

Dalam kasus di mana rotasi tidak memiliki pusat pada titik asal, asal sistem koordinat ke asal yang diberikan baru harus ditransfer, untuk memutar gambar yang memiliki asal pusat tersebut.

Misalnya, jika titik p (-5,2) rotasi 90 diterapkan^{salah satu}, Sekitar asal dan dalam arti positif koordinat barunya adalah (-2,5).

Dengan refleksi atau simetri

Adalah transformasi yang menginvestasikan poin dan angka pesawat. Investasi ini dapat sehubungan dengan suatu titik atau juga dapat sehubungan dengan suatu garis.

Dengan kata lain, dalam jenis transformasi ini setiap titik dalam gambar asli dikaitkan dengan titik lain (gambar) dari sosok homolog, sehingga titik dan gambarnya berada pada jarak yang sama dari garis yang disebut sumbu simetri.

Dengan demikian, bagian kiri gambar akan menjadi cerminan dari sisi kanan, tanpa mengubah bentuk atau dimensinya. Simetri mengubah gambar yang sama tetapi secara terbalik, seperti yang dapat dilihat pada gambar berikut:

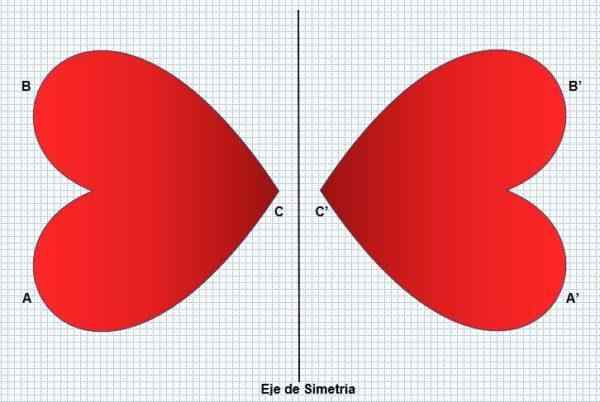
Simetri hadir dalam banyak aspek, seperti beberapa tanaman (bunga matahari), hewan (merak) dan fenomena alam (kepingan salju). Manusia mencerminkannya di wajahnya, yang dianggap sebagai faktor kecantikan. Refleksi atau simetri dapat dari dua jenis:

Simetri Tengah

Transformasi yang terjadi sehubungan dengan suatu titik, di mana gambar dapat mengubah orientasinya. Setiap titik dalam gambar asli dan gambarnya berada pada jarak yang sama dari suatu titik atau, disebut pusat simetri. Simetri adalah pusat saat:

• Baik titik maupun citra serta pusatnya termasuk dalam garis yang sama.
• Dengan rotasi 180^{salah satu} dari pusat atau gambar yang sama dengan yang asli diperoleh.
• Stroke dari gambar awal sejajar dengan sapuan sosok yang terbentuk.
• Arti dari angka tersebut tidak berubah, itu akan selalu dalam jadwal.

Dapat melayani Anda: berapa banyak yang harus Anda tambahkan ke 3/4 untuk mendapatkan 6/7?

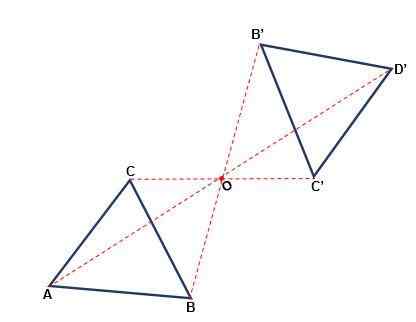Simetri aksial

Transformasi ini terjadi sehubungan dengan sumbu simetri, di mana setiap titik dalam gambar awal dikaitkan dengan titik lain dalam gambar dan ini berada pada jarak yang sama dengan sumbu simetri. Simetri adalah aksial saat:

• Segmen yang bergabung dengan suatu titik dengan gambarnya tegak lurus terhadap sumbu simetrinya.
• Angka -angka mengubah maknanya mengenai pergantian atau arah waktu.
• Dengan membagi gambar dengan garis pusat (sumbu simetri), salah satu bagian yang dihasilkan bertepatan sepenuhnya dengan bagian yang lain.

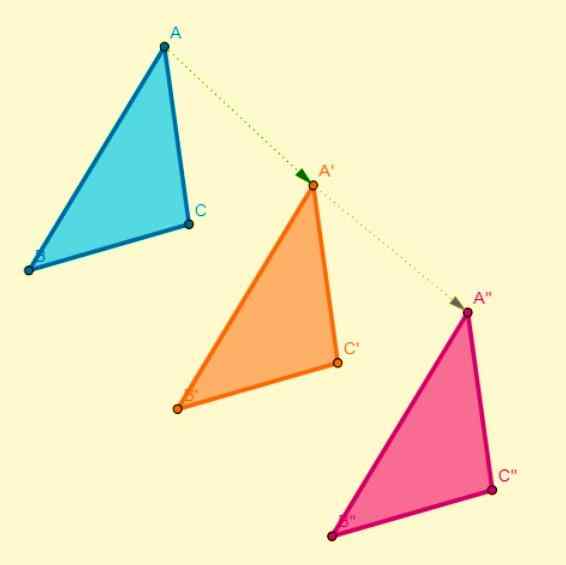
Komposisi

Komposisi transformasi isometrik mengacu pada aplikasi berurutan dari transformasi isometrik pada gambar yang sama.

Komposisi terjemahan

Komposisi dua terjemahan menghasilkan terjemahan lain. Saat dilakukan pada bidang, pada sumbu horizontal (x) hanya koordinat dari sumbu tersebut berubah, sedangkan koordinat sumbu vertikal (Y) tetap sama, dan sebaliknya.

Komposisi rotasi

Komposisi dua putaran dengan pusat yang sama menghasilkan belokan lain, yang memiliki pusat yang sama dan yang amplitudo akan menjadi jumlah amplitudo dari dua belokan.

Jika pusat belokan memiliki pusat yang berbeda, potongan dua segmen titik yang sama akan menjadi pusat rotasi.

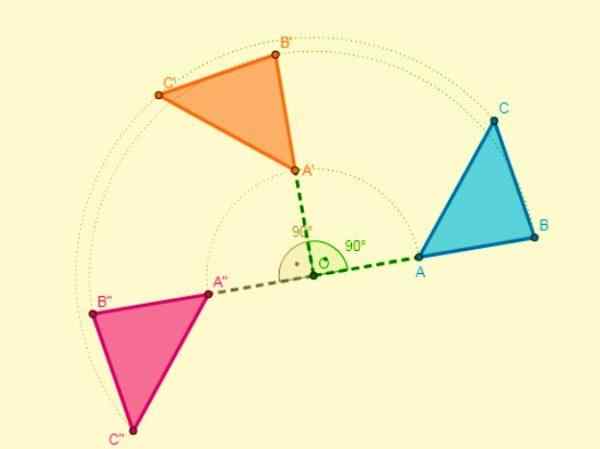
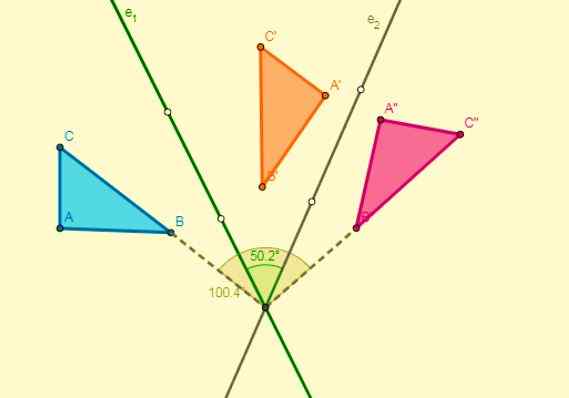
Komposisi simetri

Dalam hal ini, komposisi akan tergantung pada bagaimana itu diterapkan:

• Jika simetri yang sama diterapkan dua kali, hasilnya akan menjadi identitas.
• Jika dua simetri diterapkan sehubungan dengan dua sumbu paralel, hasilnya akan diterjemahkan, dan perpindahannya adalah dua kali jarak sumbu tersebut:

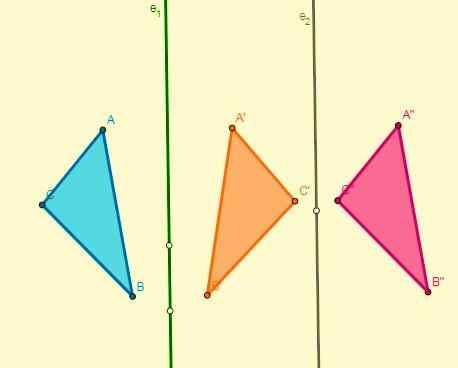
• Jika dua simetri diterapkan sehubungan dengan dua sumbu yang dipotong pada titik O (tengah), rotasi dengan pusat akan diperoleh dan sudutnya akan dua kali sudut yang terbentuk sumbu: