Fourier Transform Properties, Aplikasi, Contoh

Itu Transformasi Fourier Ini adalah metode kecukupan analitik yang berorientasi pada fungsi yang dapat diintegruk milik keluarga TRansformed komprehensif. Itu terdiri dari redefinisi fungsi F (t) dalam hal cos (t) dan sen (t).

Identitas trigonometri fungsi -fungsi ini, bersama dengan derivasi dan karakteristik antidivasi, berfungsi untuk mendefinisikan transformasi Fourier melalui fungsi kompleks berikut:

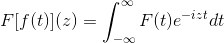
Yang terpenuhi sementara ekspresi masuk akal, yaitu, ketika integral yang tidak tepat konvergen. Secara aljabar dikatakan bahwa transformasi Fourier adalah homeomorfisme linier.

Fungsi apa pun yang dapat dikerjakan dengan transformasi Fourier harus menyajikan nol di luar parameter yang ditentukan.

[TOC]

Properti

Sumber: Pexels

Transformasi Fourier memenuhi properti berikut:

Adanya

Untuk memverifikasi keberadaan transformasi Fourier menjadi fungsi F (t) yang didefinisikan dalam bangsawan R, 2 aksioma berikut harus dipenuhi:

1. f (t) terus menerus berkeping -keping untuk semuanya R
2. f (t) dapat diintegrasikan R

Linearitas transformasi Fourier

Biarkan m (t) dan n (t) dua dua fungsi dengan fourier yang ditentukan diubah, dengan konstanta a dan b apapun.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Yang juga bergantung pada linearitas integral dari nama yang sama.

Fourier berubah dari turunan

Anda memiliki fungsi F  yang kontinu dan terintegran di semua reais, di mana:

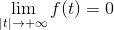
Dan turunannya F (f ') Itu kontinu dan didefinisikan pada potongan -potongan dalam segala hal R

Transformasi Fourier dari turunan ditentukan oleh integrasi oleh bagian -bagian, dengan ekspresi berikut:

F [f '(t)] (z) = IZF [f (t)] (z)

Dalam turunan yang lebih tinggi, itu akan diterapkan dengan cara yang homolog, di mana untuk semua n 1 Anda harus:

F [F ^N'(t)] (z) = (IZ)^NF [f (t)] (z)

Diferensiasi transformasi Fourier

Anda memiliki fungsi F  yang kontinu dan terintegran di semua reais, di mana:

I (d/dz)F [f (t)] (z) = F  [T .  f (t)] (z)

Fourier berubah dari terjemahan

Untuk semua θ yang termasuk dalam satu set dan T Itu milik set S ', Anda harus:

F [ τ_ke θ] =  Dan^-Iay F [ θ]                                 F [ τ_keT ] =  Dan^-IAX  F [ T]   

Dengan  τ_ke  bekerja sebagai operator terjemahan pada vektor untuk.

Terjemahan transformasi Fourier

Untuk semua θ yang termasuk dalam satu set dan T Itu milik set S ', Anda harus:

τ_ke F [θ] =  F [Dan^-IAX.θ]                                τ_ke F [t ] =  F [Dan^-Iay . T]

Dapat melayani Anda: hypercubo: definisi, dimensi, koordinat, dibuka

Untuk semua ke yang termasuk dalam R

Transformasi Fourier dari grup skala

Untuk semua θ yang milik satu set. T itu milik set S '

λ milik R - 0  Kamu harus:

F [θ (λx)] = (1 / | λ |) F [θ] (Dan/λ)                 

F [T (λx)] = (1 / | λ |) F [T] (dan/λ)

Ya F Ini adalah fungsi kontinu dan murni yang dapat diintegrasikan, di mana a> 0. Jadi:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

Untuk menunjukkan hasil ini, kita dapat melanjutkan dengan perubahan variabel.

Saat t → + lalu s = at → + ∞

Saat t → - lalu s = at → - ∞

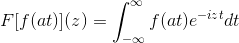
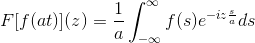
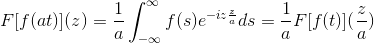
Simetri

Untuk mempelajari simetri transformasi Fourier.

Anda memiliki θ dan Δ milik S. Dari sana dapat disimpulkan bahwa:

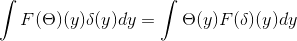
Memperoleh

1 / (2π)^D  F [θ ], F [Δ] Identitas parseval

1 / (2π)^D/2  || F [θ ] ||_L²_R^D     Formula Plancherel

Fourier berubah dari suatu produk menjadi konvolusi

Mengejar tujuan serupa yang dalam transformasi Laplace, konvolusi fungsi mengacu pada produk di antara transformasi Fourier -nya.

Ini memiliki F dan G sebagai 2 fungsi terbatas, didefinisikan dan sepenuhnya diintegrasikan:

F (f *g) = f (f) . F (g)

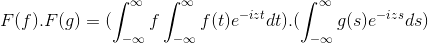
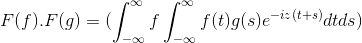
Kemudian saat membuat perubahan variabel

t + s = x; Integral ganda integral ganda dilanjutkan

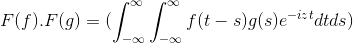
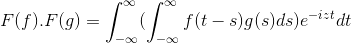
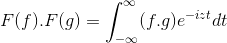
F (f) . F (g) = f (f . G)

Kontinuitas dan jatuh dalam tak terbatas

Untuk semua θ itu milik R, f [ θ] mematuhi kriteria fungsi kontinu terbatas di R^D.

Juga F [ θ] (y) → 0 di C si | y | → ∞

Sejarah

Konsep matematika ini disajikan oleh Joseph B. Fourier pada tahun 1811 saat mengembangkan perjanjian tentang Penyebaran panas. Itu dengan cepat diadopsi oleh berbagai cabang sains dan teknik.

Itu ditetapkan sebagai alat kerja utama dalam studi persamaan dengan turunan parsial, membandingkan bahkan dengan hubungan kerja antara Laplace mengubah persamaan diferensial biasa.

Untuk apa transformasi Fourier?

Ini terutama berfungsi untuk persamaan yang signifikan, sementara mengubah ekspresi yang diturunkan menjadi elemen listrik, yang menunjukkan ekspresi diferensial dalam bentuk polinomial yang dapat diintegruk.

Dalam optimasi, modulasi dan pemodelan hasilnya bertindak sebagai ekspresi standar, menjadi sumber daya yang sering untuk rekayasa setelah beberapa generasi.

Seri Fourier

Mereka didefinisikan seri dalam hal cosen dan payudara; Mereka berfungsi untuk memfasilitasi pekerjaan dengan fungsi periodik umum. Ketika diterapkan mereka adalah bagian dari teknik resolusi persamaan diferensial parsial dan biasa.

Itu dapat melayani Anda: fungsi variabel nyata nyata dan representasi grafisnya

Seri Fourier bahkan lebih umum daripada seri Taylor, karena mereka mengembangkan fungsi diskontinua periodik yang tidak memiliki representasi dalam seri Taylor.

Bentuk lain dari seri Fourier

Untuk secara analitis memahami transformasi Fourier itu penting.

-Seri Fourier pada fungsi periode 2L

Berkali-kali perlu untuk mengadaptasi struktur seri Fourier, ke fungsi periodik yang periodenya adalah p = 2l> 0 dalam interval [-l, l].

-Seri Fourier dalam fungsi genap dan aneh

Interval [-π, π] dipertimbangkan yang menawarkan keuntungan saat mengambil keuntungan dari karakteristik simetris fungsi.

Jika f adalah torsi, seri Fourier didirikan sebagai serangkaian cosenos.

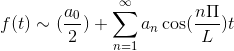
Jika f aneh, seri Fourier ditetapkan sebagai serangkaian payudara.

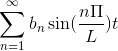
-Notasi kompleks dari seri Fourier

Jika Anda memiliki fungsi f (t), yang memenuhi semua persyaratan yang dikembangkan dari seri Fourier, dimungkinkan untuk menunjukkannya dalam interval [-t, t] menggunakan notasi kompleksnya:

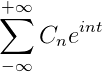
Aplikasi

Sumber: Pexels

Perhitungan solusi mendasar

Transformasi Fourier adalah alat yang ampuh dalam studi persamaan diferensial parsial tipe linier dengan koefisien konstan. Berlaku untuk fungsi dengan domain yang tidak terbatas sama.

Seperti Transformasi Laplace, transformasi Fourier mengubah fungsi turunan parsial, menjadi persamaan diferensial biasa lebih mudah untuk beroperasi.

Masalah Cauchy untuk persamaan panas menyajikan bidang penerapan transformasi Fourier yang sering Dirichlet panas atau inti inti.

Mengenai perhitungan solusi fundamental, kasus -kasus berikut disajikan di tempat yang umum untuk menemukan transformasi Fourier:

-Persamaan Laplace

-Persamaan panas

-Persamaan Schrödinger

-Persamaan Gelombang

Teori sinyal

Alasan umum untuk penerapan transformasi Fourier di cabang ini sebagian besar disebabkan oleh dekomposisi khas sinyal sebagai tumpang tindih tak terbatas dari sinyal yang lebih mudah diobati.

Ini bisa berupa gelombang suara atau gelombang elektromagnetik, transformasi Fourier mengekspresikannya dalam gelombang sederhana tumpang tindih. Representasi ini cukup sering dalam rekayasa listrik.

Dapat melayani Anda: garis vertikal

Di sisi lain, mereka adalah contoh penerapan transformasi Fourier di bidang teori sinyal:

-Masalah identifikasi sistem. Mapan f dan g

-Masalah dengan konsistensi sinyal output

-Masalah dengan pemfilteran sinyal

Contoh

Contoh 1

Tentukan transformasi Fourier untuk ekspresi berikut:

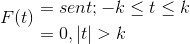
Kami juga dapat mewakili itu sebagai berikut:

F (t) = Dosa (t) [h_{(T + k)} - H_{(T - k)} ]

Denyut nadi persegi panjang didefinisikan:

p (t) = h_{(T + k)} - H_{(T - k)}

Transformasi Fourier diterapkan pada ekspresi berikutnya yang menyerupai teorema modulasi.

f (t) = p (t) sin (t)

Di mana: F [w] = (1/2) i [p (w + 1) - p (w - 1)]

Dan transformasi Fourier didefinisikan oleh:

F [w] =  (1/2) I [(2/2W+1) Sen (k (w+1)) - (2/2w+1) Sen (k (w-1))]

Contoh 2

Tentukan transformasi Fourier untuk ekspresi:

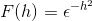Menurut definisi kami mengekspresikan transformasi sebagai berikut

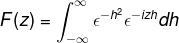
Karena f (h) adalah fungsi yang rata, itu dapat ditegaskan itu

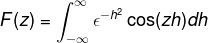Turun di dalam integral sehubungan dengan Z, ekspresi dapat ditulis ulang. Langkah ini signifikan dalam pekerjaan dengan persamaan diferensial.

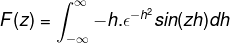
Integrasi oleh bagian diterapkan dengan memilih variabel dan perbedaannya sebagai berikut

u = sin (zh) du = z cos (zh) dh

dv = h (e^-H)²                       V = (e^-H)² / 2

Menggantinya

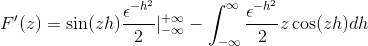
Setelah mengevaluasi di bawah teorema perhitungan mendasar

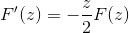
Menerapkan pengetahuan sebelumnya yang terkait dengan persamaan diferensial dari urutan pertama, ekspresi dilambangkan sebagai

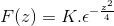
Untuk mendapatkan k yang kami evaluasi 

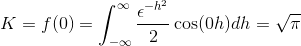
Akhirnya, transformasi Fourier didefinisikan sebagai

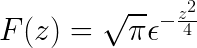
Latihan yang diusulkan

• Tentukan ekspresi transformasi Fourier
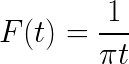
• Selesaikan integral yang tidak tepat berikut menggunakan kesetaraan Pareseval
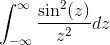
• Dapatkan transformasi ekspresi w/(1+w²)

Referensi

1. Duoandikoetxea zuazo, j., Analisis Fourier. Addison- Wesley Iberoamericana, Universitas Otonomi Madrid, 1995.
2. Singa, J. L., Analisis Matematika dan Metode Numerik untuk Sains dan Teknologi. Springer-Verlag, 1990.
3. Lieb, e. H., Kernel Gaussian hanya memiliki maksimal Gaussian. Menciptakan. Matematika. 102, 179-208, 1990.
4. Dym, h., McKean, h. P., Seri Fourier dan Integral. Academic Press, New York, 1972.
5. Schwartz, l., Distribusi Théorie des. Ed. Hermann, Paris, 1966.