Fourier Discreet Transformed Properties, Aplikasi, Contoh

Itu Fourier Discreet diubah Ini adalah metode numerik yang digunakan untuk mendefinisikan sampel yang terkait dengan frekuensi spektral yang membentuk sinyal. Mempelajari fungsi -fungsi berkala dalam parameter tertutup, melempar sebagai akibatnya sinyal bijaksana lainnya.

Untuk mendapatkan transformasi bijaksana furier dari titik n, pada sinyal bijaksana, 2 kondisi berikut pada urutan harus dipenuhi X [n]

 x [n] = 0   N n - 1

Memenuhi persyaratan ini, transformasi diskrit Fourier dapat didefinisikan sebagai

Tdf

Transformasi Discreet Fourier dapat didefinisikan sebagai pengambilan sampel pada titik N dari transformasi Fourier.

[TOC]

Interpretasi transformasi Discreet Fourier

Sumber: Pexels

Ada 2 sudut pandang dari mana hasil yang diperoleh pada urutan x dapat ditafsirkan_S[n] Melalui transformasi Discreet Fourier.

-Yang pertama sesuai dengan koefisien spektral, sudah diketahui dengan seri Fourier. Itu diamati dalam sinyal periodik diskrit, dengan sampel bertepatan dengan urutan x_S[N].

-Yang kedua adalah tentang spektrum sinyal aperiadic yang bijaksana, dengan sampel yang sesuai dengan urutan x_S[N].

Transformasi Discreet adalah pendekatan untuk spektrum sinyal analog asli. Fasenya tergantung pada momen pengambilan sampel, sedangkan besarnya tergantung pada interval pengambilan sampel.

Properti

Fondasi aljabar struktur merupakan dasar logis dari bagian berikut.

Linearitas

C . S_N → c . F[S_k]; Jika urutan dikalikan dengan skalar, transformnya juga akan terjadi.

T_N + V_N = F [t_k]+F [v_k]; Transformasi jumlah sama dengan jumlah yang ditransformasikan.

Dualitas

F [s_N] → (1/n) s_-K; Jika transformasi Discreet dari Fourier ditarik kembali ke ekspresi yang sudah diubah, ekspresi yang sama diperoleh, pendakian di N terbalik sehubungan dengan sumbu vertikal.

Lilitan

Mengejar tujuan serupa yang dalam transformasi Laplace, konvolusi fungsi mengacu pada produk di antara transformasi Fourier -nya. Konvolusi ini juga berlaku untuk zaman diskrit dan bertanggung jawab atas banyak prosedur modern.

X_N * R_N → f [x_N] .F [r_N]; Transformasi konvolusi sama dengan produk yang diubah.

X_N . R_N→ f [x_N] * F [r_N]; Transformasi suatu produk sama dengan konvolusi yang ditransformasikan.

Pemindahan

X_N-m → f [x_k] e ^{-I (2π/n) km} ; Jika suksesi ditunda dalam sampel M, pengaruhnya terhadap transformasi yang bijaksana akan menjadi modifikasi sudut yang ditentukan oleh (2π/n) km.

Dapat melayani Anda: mengapa aljabar penting dalam situasi kehidupan sehari -hari tertentu?

Simetri terkonjugasi

X_T [-K] = x*_T[k] = x_T [N - k]

Modulasi

W^-nm_N . x [n] ↔ x_T[K - m]

Produk

x [n] y [n] ↔ (1/n) x_T[k]*dan_T[K]

Simetri

X [-n] ↔ x_T[-K] = x*_T[K]

Mengkonjugasikan

x*[n] ↔ x*_T[-K]

Persamaan Parseval 

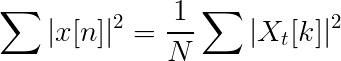
Persamaan dan perbedaan dengan transformasi Fourier

Sehubungan dengan transformasi konvensional Fourier, ia memiliki beberapa persamaan dan perbedaan. Transformasi Fourier mengubah urutan menjadi garis kontinu. Dengan cara ini dikatakan bahwa hasil dari variabel Fourier adalah fungsi variabel nyata yang kompleks.

Transformasi Discreet Fourier, tidak seperti, menerima sinyal bijaksana dan mengubahnya menjadi tanda diam -diam lainnya, yaitu urutan.

Apa penggunaan transformasi Discreet Fourier?

Mereka terutama berfungsi untuk persamaan yang signifikan, sambil mengubah ekspresi yang diturunkan menjadi elemen listrik. Menunjukkan ekspresi diferensial dalam bentuk polinomial yang dapat diintegrasikan.

Dalam optimasi, modulasi dan pemodelan hasilnya bertindak sebagai ekspresi standar, menjadi sumber daya yang sering untuk rekayasa setelah beberapa generasi.

Sumber: Pixabay

Sejarah

Konsep matematika ini disajikan oleh Joseph B. Fourier pada tahun 1811, saat mengembangkan perjanjian tentang Penyebaran panas. Itu dengan cepat diadopsi oleh berbagai cabang sains dan teknik.

Itu ditetapkan sebagai alat kerja utama dalam studi persamaan dengan turunan parsial, membandingkan bahkan dengan hubungan kerja antara Laplace mengubah persamaan diferensial biasa.

Fungsi apa pun yang dapat dikerjakan dengan transformasi Fourier harus menyajikan nol di luar parameter yang ditentukan.

Fourier Discreet diubah dan terbalik

Transformasi diam -diam diperoleh melalui ekspresi:

Setelah urutan bijaksana x [n]

Kebalikan dari transformasi Discreet Fourier didefinisikan melalui ekspresi:

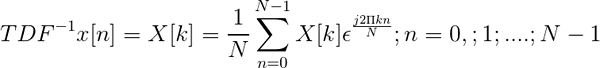TDF terbalik

Ini memungkinkan begitu Discreet diubah, tentukan urutan dalam domain waktu x [n].

Perhiasan

Proses parameterisasi yang sesuai dengan transformasi diskrit Fourier terletak pada Cub. Untuk mengerjakan transformasi, kita harus membatasi urutan waktu. Dalam banyak kasus, sinyal yang dimaksud tidak memiliki batasan ini.

Suksesi yang tidak memenuhi kriteria ukuran untuk diterapkan pada transformasi bijaksana, dapat dikalikan dengan fungsi "jendela" v [n], mendefinisikan perilaku suksesi dalam parameter yang dikendalikan.

Dapat melayani Anda: permutasi melingkar: demonstrasi, contoh, latihan terselesaikan

X [n] . V [n]

Lebar spektrum akan tergantung pada lebar jendela. Seiring meningkatnya lebar jendela, yang diubah yang dihitung akan lebih sempit.

Aplikasi

Perhitungan solusi mendasar

Transformasi Discreet Fourier adalah alat yang ampuh dalam mempelajari suksesi diskrit.

Transformasi Discreet Fourier mengubah fungsi variabel kontinu, menjadi transformasi variabel diskrit.

Masalah Cauchy untuk Persamaan Panas menyajikan bidang penerapan transformasi Discreet Fourier. Dimana fungsinya dihasilkan Dirichlet panas atau inti inti, yang berlaku untuk pengambilan sampel nilai dalam parameter yang ditentukan.

Teori sinyal

Alasan umum untuk penerapan transformasi diskrit Fourier dalam cabang ini sebagian besar disebabkan oleh dekomposisi khas sinyal sebagai tumpang tindih tak terbatas dari sinyal yang lebih mudah diobati.

Ini bisa berupa gelombang suara atau gelombang elektromagnetik, transformasi diskrit Fourier mengekspresikannya dalam gelombang sederhana tumpang tindih. Representasi ini cukup sering dalam rekayasa listrik.

Seri Fourier

Mereka didefinisikan seri dalam hal cosenos dan payudara. Mereka berfungsi untuk memfasilitasi pekerjaan dengan fungsi periodik umum. Ketika diterapkan mereka adalah bagian dari teknik resolusi persamaan diferensial parsial dan biasa.

Seri Fourier bahkan lebih umum daripada seri Taylor, karena mereka mengembangkan fungsi diskontinua periodik yang tidak memiliki representasi dalam seri Taylor.

Bentuk lain dari seri Fourier

Untuk secara analitis memahami transformasi Fourier, itu penting.

-Seri Fourier pada fungsi periode 2L:

Berkali-kali perlu untuk mengadaptasi struktur seri Fourier, ke fungsi periodik yang periodenya adalah p = 2l> 0 dalam interval [-l, l].

-Seri Fourier dalam fungsi genap dan aneh

Interval [-π, π] dipertimbangkan yang menawarkan keuntungan saat mengambil keuntungan dari karakteristik simetris fungsi.

Dapat melayani Anda: Himpunan terbatas: properti, contoh, latihan terpecahkan

Jika f adalah torsi, seri Fourier didirikan sebagai serangkaian cosenos.

Jika f aneh, seri Fourier ditetapkan sebagai serangkaian payudara.

-Notasi kompleks dari seri Fourier

Jika Anda memiliki fungsi f (t), yang memenuhi semua persyaratan dari seri Fourier, dimungkinkan untuk menunjukkannya dalam interval [-t, t] menggunakan notasi kompleksnya: 

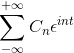
Contoh

Mengenai perhitungan solusi mendasar, contoh -contoh berikut disajikan:

Persamaan Laplace

Persamaan panas

Persamaan Schrödinger

Persamaan Gelombang

Di sisi lain, ada contoh penerapan transformasi diskrit Fourier di bidang teori sinyal:

-Masalah identifikasi sistem. Mapan f dan g

-Masalah dengan konsistensi sinyal output

-Masalah dengan pemfilteran sinyal

Latihan

Latihan 1

Hitung transformasi Discreet Fourier untuk suksesi berikut.

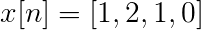
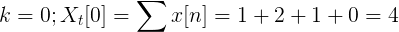
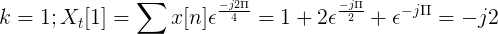
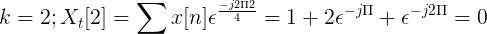
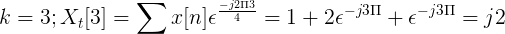
X [n] TDF dapat didefinisikan sebagai:

X_T[k] = 4, -j2, 0, j2 untuk k = 0, 1, 2, 3

Latihan 2

Itu ingin menentukan melalui algoritma digital sinyal spektral yang ditentukan oleh ekspresi x (t) = e^-T. Di mana koefisien permintaan frekuensi maksimum adalah f_M= 1Hz. Harmonik sesuai dengan F = 0.3 Hz. Kesalahannya dibatasi hingga kurang dari 5%. Menghitung F_S , D dan n.

Dengan mempertimbangkan teorema pengambilan sampel F_S = 2f_M = 2 Hz

Resolusi frekuensi F₀ = 0.1 Hz, di mana d = 1/0,1 = 10s diperoleh

0.3 Hz adalah frekuensi yang sesuai dengan indeks k = 3, di mana n = 3 × 8 = 24 sampel. Menunjukkan itu F_S = N/d = 24/10 = 2.4> 2

Karena tujuannya adalah untuk mencapai nilai yang paling tidak mungkin untuk n, nilai -nilai berikut dapat dianggap sebagai solusi:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33S

K = 1

N = 1 × 8 = 8

Referensi

1. Menguasai Transformasi Fourier Discrete dalam satu, dua atau beberapa dimensi: jebakan dan artefak. Isaac Amidor. Springer Science & Business Media, 19 Jul. 2013
2. DFT: Manual Pemilik untuk Transformasi Fourier Discrete. William L. Briggs, Van Emden Henson. Siam, 1 Januari. sembilan belas sembilan puluh lima
3. Pemrosesan Sinyal Digital: Teori dan Praktek. D. Sundararajan. World Scientific, 2003
4. Mengubah dan algoritma cepat untuk analisis dan representasi sinyal. Guoan Bi, Yonghong Zeng. Media Sains & Bisnis Springer, 6 Desember. 2012
5. Transformasi Fourier Diskrit dan Berkelanjutan: Analisis, Aplikasi dan Algoritma Cepat. Eleanor Chu. CRC Press, 19. 2008