Properti Escaleno Trapezio, Rumus dan Persamaan, Contoh

A rekstok gantung sisi tak sama panjang Ini adalah poligon empat -sisi, dua di antaranya sejajar satu sama lain, dan dengan empat sudut interior dari ukuran yang berbeda.

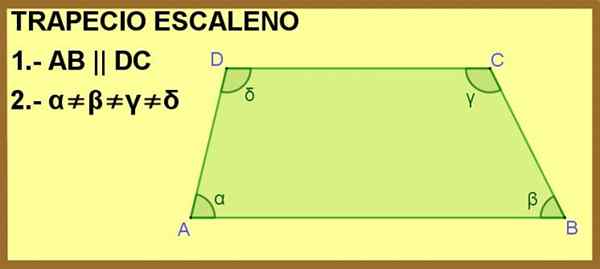
ABCD Quadrilateral ditampilkan, di mana sisi AB dan DC sejajar satu sama lain. Dengan ini, itu cukup untuk menjadikannya trapeze, tetapi selain itu, sudut interior α, β, γ dan Δ semuanya berbeda, oleh karena itu trapesiumnya adalah Escalano.

Gambar 1. ABCD Quadrilateral adalah trapeze untuk kondisi 1 dan scalene untuk kondisi 2. Sumber: f. Zapata.

[TOC]

Elemen trapect scaleno

Di bawah elemen paling khas:

-Basis dan sisi: Sisi paralel trapesium adalah pangkalannya dan dua sisi non -paralel adalah sisi.

Dalam trapezio scalene, basisnya memiliki panjang yang berbeda dan sisi juga. Namun, trapesium scalene dapat memiliki sisi panjang yang sama dengan dasar.

-Median: Itu adalah segmen yang bergabung dengan titik tengah sisi.

-Diagonal: Diagonal dari trapeze adalah segmen yang bergabung dengan dua simpul yang berlawanan. Trapeze, seperti setiap segi empat, memiliki dua diagonal. Di scalene trapezio mereka memiliki panjang yang berbeda.

Trapesium lainnya

Selain escaleno trapezio, ada trapesium khusus lainnya: trapesium persegi panjang dan trapesium isosceles.

Trapeze adalah persegi panjang ketika salah satu sudutnya lurus, sedangkan trapezio isosceles memiliki sisi dengan panjang yang sama.

Bentuk trapesium memiliki banyak aplikasi di tingkat desain dan industri, seperti dalam konfigurasi sayap pesawat, bentuk benda sehari -hari seperti tabel, cadangan kursi, wadah, dompet, cetakan tekstil dan banyak lagi.

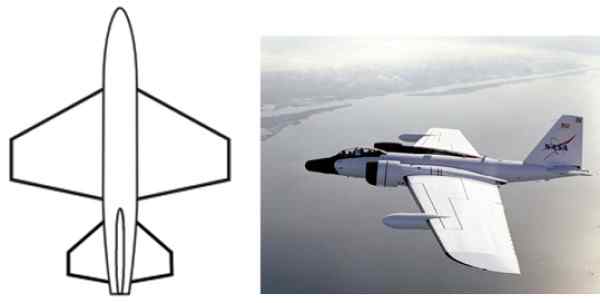Gambar 2. Bentuk trapesium adalah umum dalam konfigurasi pesawat Alar. Sumber: Wikimedia Commons.

Properti

Selanjutnya, sifat -sifat trapesium pendakian terdaftar, banyak di antaranya luas untuk jenis trapesium lainnya. Berikut ini, ketika Anda berbicara tentang "Trapezio", properti akan berlaku untuk segala jenis, termasuk Scalene.

1. Median trapesium, yaitu segmen yang menyatukan titik tengah dari sisi non -paralelnya, sejajar dengan pangkalan mana pun.

2.- Median trapesium memiliki panjang yang merupakan semi -soum pangkalannya dan memotong diagonalnya di titik tengah.

3.- Diagonal sebuah trapeze berpotongan pada titik yang membaginya menjadi dua bagian yang sebanding dengan rasio basis.

4.- Jumlah kotak diagonal trapeze sama dengan jumlah kotak dari sisinya ditambah produk ganda dari pangkalannya.

5.- Segmen yang bergabung dengan titik -titik pertengahan -diagonal memiliki panjang yang sama dengan semi -referensi pangkalan.

Dapat melayani Anda: fungsi suntikan: apa yang terdiri dari, untuk apa dan contohnya

6.- Sudut yang berdekatan dengan samping adalah tambahan.

7.- Dalam trapeze scalene, panjang diagonalnya berbeda.

8.- Trapeze memiliki lingkar terdaftar hanya jika jumlah pangkalannya sama dengan jumlah sisinya.

9.- Jika trapeze memiliki lingkar terdaftar, maka sudut dengan simpul di tengah lingkar dan sisi yang melewati ujung lateral trapeze lurus.

10.- Trapeze escaleno tidak memiliki keliling terbatas, satu -satunya jenis trapeze yang jika ada adalah isosceles.

Rumus dan Persamaan

Hubungan trapeze pendakian berikut dirujuk ke gambar berikut ini.

1.- Jika ae = ed dan bf = fc → ef || AB dan EF || Dc.

2.- EF = (ab + dc)/2 yaitu: m = (a + c)/2.

3.- Di = ib = D₁ /2 dan ag = gc = d₂ /2.

4.- Dj / jb = (c / a) Demikian pula cj / ja = (c / a).

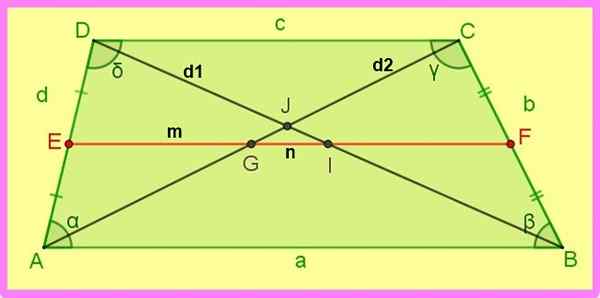Gambar 3. Median dan diagonal trapesium scalene. Sumber: f. Zapata.

5.- Db² + Ac² = Iklan² + Bc² + 2 ab ∙ dc 

Setara:

D₁² + D₂² = d² + B² + 2 A ∙ C

6.- GI = (AB - DC)/2

Artinya:

n = (a - c)/2

7.- α + Δ = 180⁰ dan β + γ = 180⁰

8.- Jika α ≠ β ≠ γ ≠ Δ maka d1 ≠ d2.

9.- Gambar 4 menunjukkan trapesium scalene yang memiliki keliling terdaftar, dalam hal ini dipenuhi bahwa:

A + c = d + b

10.- Dalam ABCD Escalene Trapezoid dengan pusat terdaftar dari pusat atau berikut ini juga terpenuhi:

∡Aod = ∡Boc = 90⁰

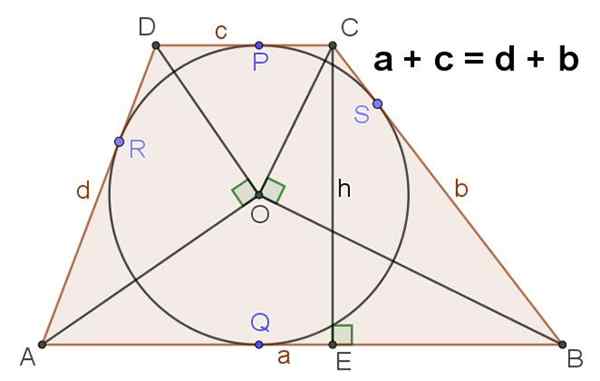Gambar 4. Jika dalam trapeze diverifikasi bahwa jumlah pangkalannya sama dengan jumlah sisi, maka ada keliling yang tertulis dalam hal yang sama. Sumber: f. Zapata.

Tinggi

Ketinggian trapeze didefinisikan sebagai segmen yang berubah dari titik dasar tegak lurus ke basis yang berlawanan (atau ekstensi).

Semua ketinggian trapeze memiliki ukuran yang sama, jadi sebagian besar waktu ketinggian kata mengacu pada pengukurannya. Singkatnya, tinggi adalah jarak atau pemisahan antara pangkalan.

Tinggi H dapat ditentukan jika panjang sisi dan salah satu sudut yang berdekatan dengan sisi diketahui:

H = d sin (α) = d sin (γ) = b sin (β) = b sin (δ)

Median

Ukuran median m dari trapesium adalah semi -bodi pangkalan:

M = (a + b)/2

Diagonal

D₁ = √ [a² + D² - 2 ∙ a ∙ d ∙ cos (α)]

D₂= √ [a² + B² - 2 ∙ A ∙ B ∙ cos (β)]

Itu juga dapat dihitung jika hanya panjang trapesium yang diketahui:

D₁ = √ [b² + A ∙ C - A (b² - D²)/(a - c)]

D₂ = √ [D² + A ∙ C - A (D² - B²)/(a - c)]

Perimeter

Perimeter adalah panjang total kontur, yaitu, jumlah dari semua sisinya:

Dapat melayani Anda: variabel acak diskrit

P = A + B + C + D

Daerah

Area trapesium adalah semi -body dari pangkalannya dikalikan dengan tinggi:

A = h ∙ (a + b)/2

Ini juga dapat dihitung jika median M dan tinggi diketahui:

A = m ∙ h

Jika hanya panjang sisi trapesium yang diketahui, area tersebut dapat ditentukan oleh formula Herón untuk trapesium:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]

Di mana s adalah semi -perimeter: s = (a+b+c+d)/2.

Hubungan lain untuk pendakian pendakian

Potongan median dengan diagonal dan paralel yang melewati persimpangan diagonal, menimbulkan hubungan lain.

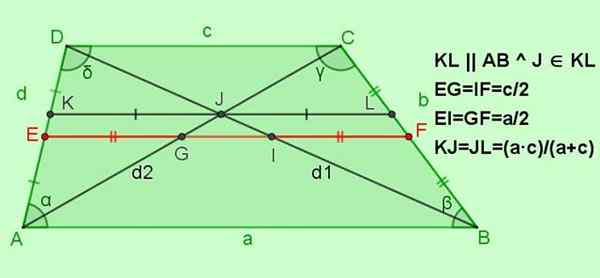Gambar 5. Hubungan lain untuk pendakian pendakian. Sumber: f. Zapata.

-Hubungan untuk median EF

EF = (A+C)/2; Misalnya = if = c/2; Ei = gf = a/2

-Hubungan untuk segmen paralel ke pangkalan KL, dan itu melewati titik Persimpangan j dari diagonal

Ya KL || Ab || Dc dengan j ∈ Kl, lalu kJ = jl = (a ∙ c)/(a+c)

Konstruksi trapesium scalene dengan aturan dan kompas

Mengingat basis panjangnya ke Dan C, menjadi A> C dan dengan sisi panjang B dan D, makhluk b> d, Kami melanjutkan mengikuti langkah -langkah ini (lihat Gambar 6):

1.- Dengan aturan, segmen AB terbesar ditarik.

2.- Dari SE dan AB, titik P ditandai sehingga ap = c.

3.- Dengan kompas dengan C dan Radio D Center, busur ditarik.

4.- Itu dibuat tengah di B dengan Radio B menggambar busur yang menafsirkan busur yang disusun pada langkah sebelumnya. Kami menyebutnya titik persimpangan.

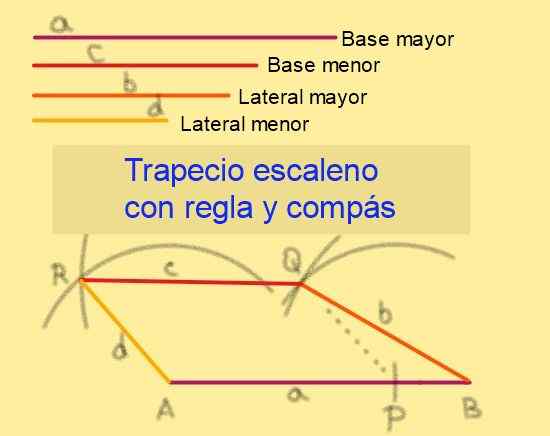Gambar 6. Konstruksi Escaleno Trapecio diberikan sisi. Sumber: f. Zapata.

5.- Dengan pusat dalam menggambar busur jari -jari.

6.- Dengan pusat untuk menggambar busur jari -jari yang dicegat ke busur yang disusun pada langkah sebelumnya. Itu akan disebut r ke titik pemotongan.

7.- Segmen BQ, QR dan RA ditarik dengan aturan.

8.- ABQR Quadrilateral adalah trapesium scalene, karena APQR adalah jajaran genjang, yang menjamin bahwa AB || Qr.

Contoh

Panjang berikut diberikan dalam cm: 7, 3, 4 dan 6.

a) Tentukan apakah dengan mereka Anda dapat membangun trapeze skalen yang dapat membatasi lingkar.

b) Temukan perimeter, area, panjang diagonal dan ketinggian trapeze tersebut, serta jari -jari keliling terdaftar.

- Solusi untuk

Menggunakan segmen panjang 7 dan 3 sebagai basis dan panjang 4 dan 6 sebagai sisi, trapesium skalen dapat dibangun menggunakan prosedur yang dijelaskan pada bagian sebelumnya.

Kita perlu memeriksa apakah memiliki lingkar terdaftar, tetapi mengingat properti (9):

Dapat melayani Anda: prisma heksagonal

Trapeze memiliki lingkar terdaftar hanya jika jumlah pangkalannya sama dengan jumlah sisinya.

Kami memang melihat itu:

7 + 3 = 4 + 6 = 10

Kemudian kondisi keliling tertulis terpenuhi.

- Solusi b

Perimeter

Perimeter P diperoleh dengan menambahkan sisi. Sebagai pangkalan total 10 dan sisi juga, perimeter adalah:

P = 20 cm

Daerah

Untuk menentukan area tersebut, hanya diketahui sisi -sisinya, hubungan itu diterapkan:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]

Di mana s adalah semi -persper

S = (A+B+C+D)/2.

Dalam kasus kami, semi -perimeter bernilai s = 10 cm. Setelah mengganti nilai masing -masing:

A = 7 cm; B = 6 cm; C = 3 cm; D = 4 cm

Tersisa:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Tinggi

Tinggi H terkait dengan area A melalui ekspresi berikut:

A = (a+c) ∙ h/2, di mana tinggi dapat diperoleh dengan clearance:

H = 2a / (a+c) = 2 * 19.84 / 10 = 3.968 cm.

Radio Lingkar Terdaftar

Radius keliling terdaftar bernilai setengah dari tinggi:

R = h/2 = 1.984 cm

Diagonal

Akhirnya ada panjang diagonal:

D₁ = √ [b² + A ∙ C - A (b² - D²)/(a - c)]

D₂ = √ [D² + A ∙ C - A (D² - B²)/(a - c)]

Mengganti nilainya dengan benar adalah:

D₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

D₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

Yaitu: D₁ = 4,69 cm dan d₂ = 8.49 cm

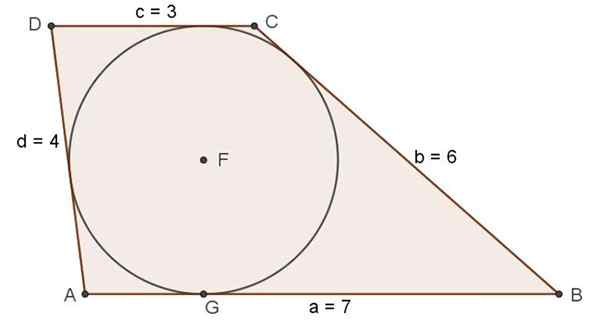Gambar 7. Scalene trapezio yang memenuhi syarat keberadaan keliling terdaftar. Sumber: f. Zapata.

Olahraga diselesaikan

Tentukan sudut interior trapesium dasar AB = A = 7, CD = C = 3 dan lateral BC = B = 6, DA = D = 4.

Larutan

Teorema kosinus dapat diterapkan untuk menentukan sudut. Sebagai contoh, sudut ∠A = α ditentukan dari segitiga ABD dengan ab = a = 7, bd = d2 = 8.49 dan da = d = 4.

Teorema kosinus yang diterapkan pada segitiga ini tetap seperti ini:

D₂² = a² + D² - 2 ∙ a ∙ d ∙ cos (α), yaitu:

72 = 49+16-56 ∙ cos (α).

Saat membersihkan, kosinus sudut α diperoleh:

Cos (α) = -1/8

Artinya α = arccos (-1/8) = 97.18⁰.

Dengan cara yang sama sudut lain diperoleh, menjadi nilai -nilainya:

β = 41.41⁰; γ = 138.59⁰ dan akhirnya δ = 82.82⁰.

Referensi

1. C. DAN. KE. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Grup Editorial Patria.
3. Freed, k. (2007). Temukan poligon. Perusahaan Pendidikan Benchmark.
4. Hendrik, v. (2013). Poligon umum. Birkhäuser.
5. Iger. (S.F.). Matematika semester pertama Tacaná. Iger.
6. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematika: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
8. Patiño, m. (2006). Matematika 5. Progreso editorial.
9. Wikipedia. Rekstok gantung. Pulih dari: is.Wikipedia.com