Karakteristik Lintasan Fisik, Jenis, Contoh dan Latihan

Itu Lintasan dalam fisika Kurva yang menggambarkan ponsel saat melewati titik -titik berturut -turut selama gerakannya. Karena ini dapat mengadopsi varian yang tak terhitung jumlahnya, sehingga mereka juga akan menjadi lintasan yang dapat diikuti oleh ponsel.

Untuk pergi dari satu tempat ke tempat lain, seseorang dapat mengambil jalan yang berbeda dan cara yang berbeda: berjalan kaki melalui trotoar di jalanan dan jalan, atau tiba dengan mobil atau sepeda motor di jalan raya. Selama perjalanan melalui hutan, pejalan kaki dapat mengikuti lintasan rumit yang mencakup belokan, memanjat atau menjatuhkan dan sampai dia melewati beberapa kali melalui titik yang sama.

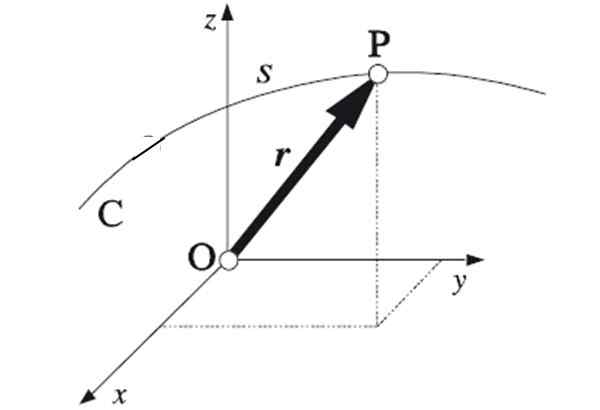Gambar 1. Bergabung dengan titik -titik ekstrem dari setiap vektor posisi lintasan diikuti oleh partikel diperoleh. Sumber: Algarabia [domain publik]

Jika titik -titik di mana ponsel bepergian mengikuti garis lurus, lintasan akan menjadi bujur. Ini adalah lintasan paling sederhana, untuk menjadi satu -dimensional. Menentukan posisi membutuhkan koordinat tunggal.

Tetapi ponsel dapat mengikuti lintasan lengkung, bisa ditutup atau dibuka. Dalam kasus ini, pemantauan posisi membutuhkan dua atau tiga koordinat. Ini adalah gerakan di bidang dan ruang masing -masing. Ini ada hubungannya dengan tautan: Membatasi kondisi material gerakan. Beberapa contoh adalah:

- Orbit yang menggambarkan planet -planet di sekitar matahari adalah lintasan berbentuk elips tertutup. Meskipun, dalam beberapa kasus, mereka dapat mendekati lingkaran, seperti dalam kasus bumi.

- Bola yang ditendang kiper dalam tendangan gawang mengikuti lintasan parabola.

- Sebuah burung dalam penerbangan menggambarkan lintasan lengkung di ruang angkasa, karena selain bergerak di pesawat, itu bisa naik atau lebih rendah pada keinginan.

Lintasan fisika dapat diekspresikan secara matematis ketika posisi seluler diketahui kapan saja. Menjadi R Vektor posisi, yang pada gilirannya memiliki koordinat X, Dan Dan z Dalam kasus paling umum dari gerakan tiga dimensi. Mengetahui fungsinya R (T) Lintasan akan sepenuhnya ditentukan.

[TOC]

Teman-teman

Secara umum, lintasan bisa menjadi kurva yang agak rumit, terutama jika Anda ingin mengekspresikan secara matematis. Oleh karena itu, ia dimulai dengan model paling sederhana, di mana ponsel bepergian dengan garis lurus atau di pesawat, yang bisa menjadi lantai atau yang lain cocok:

Gerakan dalam satu, dua dan tiga dimensi

Lintasan yang paling banyak dipelajari adalah:

- Seperti garis lurus, Saat bepergian dengan garis horizontal, vertikal atau miring. Bola yang dilemparkan secara vertikal ke atas lintasan ini atau objek yang tergelincir ke bawah oleh pesawat miring juga. Mereka adalah satu gerakan -dimensi, koordinat tunggal sudah cukup untuk menentukan posisinya sepenuhnya.

- Parabola, di mana ponsel menggambarkan busur parabola. Ini sering, karena objek apa pun yang diluncurkan secara miring di bawah aksi gravitasi (sebuah proyektil) mengikuti lintasan ini. Untuk menentukan posisi seluler, Anda harus memberikan dua koordinat: X Dan Dan.

- Bundar, terjadi ketika partikel bergerak mengikuti lingkar. Itu juga umum di alam dan praktik sehari -hari. Banyak benda sehari -hari mengikuti lintasan melingkar seperti ban, potongan mesin dan satelit di orbit, untuk memberikan beberapa contoh.

Dapat melayani Anda: Vektor Equipocent: Definisi, Notasi, Latihan

- Berbentuk bulat panjang, Objek bergerak mengikuti elips. Seperti yang dinyatakan di awal, lintasan yang diikuti planet -planet di orbit di sekitar matahari.

- Hiperbolis, Objek astronomi di bawah aksi gaya pusat (gravitasi), dapat mengikuti lintasan elips (tertutup) atau hiperbolik (terbuka), ini lebih jarang daripada yang pertama.

- Spiral, o gerakan spiral, seperti burung yang naik dalam arus termal.

- Goyangan atau pendular, Ponsel menggambarkan busur dalam gerakan perjalanan pulang pergi.

Contoh

Lintasan yang dijelaskan di bagian sebelumnya sangat berguna untuk dengan cepat mendapatkan gambaran tentang bagaimana pergerakan suatu objek. Bagaimanapun, perlu untuk mengklarifikasi bahwa lintasan ponsel tergantung pada lokasi pengamat. Ini berarti bahwa peristiwa yang sama dapat dilihat dengan cara yang berbeda, sesuai dengan di mana masing -masing berada.

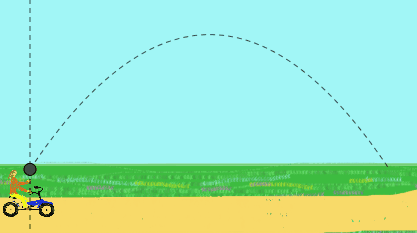
Misalnya seorang gadis pedal dengan kecepatan konstan dan melempar bola ke atas. Dia mengamati bahwa bola menggambarkan lintasan bujursangkar. 

Namun, untuk seorang pengamat yang berdiri di jalan yang melihatnya, bola akan memiliki gerakan parabola. Baginya, bola awalnya dilemparkan dengan kecepatan miring, hasil dari kecepatan di atas tangan gadis itu ditambah kecepatan sepeda.

Gambar 2. Animasi ini menunjukkan peluncuran vertikal bola yang dibuat oleh seorang gadis yang menggunakan sepeda, seperti yang dia lihat (lintasan bujursangkar) dan saat Anda melihat seorang pengamat (lintasan parabola). (Disiapkan oleh f. Zapata).

Lintasan ponsel dengan cara yang eksplisit, implisit dan parametrik

- Eksplisit, secara langsung menentukan kurva atau tempat geometris yang diberikan oleh persamaan dan (x)

- Implisit, di mana kurva dinyatakan sebagai f (x, y, z) = 0

-Parametrik, Dengan cara ini koordinat x, dan y z terjadi tergantung pada parameter yang, secara umum, dipilih seiring waktu T. Dalam hal ini, lintasan terdiri dari fungsi: x (t), dan T) Dan z (t).

Selanjutnya, dua lintasan yang sangat dipelajari dirinci dalam sinematik: lintasan parabola dan lintasan melingkar.

Diluncurkan dalam ruang hampa

Objek (proyektil) dilemparkan membentuk sudut A dengan horizontal dan dengan kecepatan awal v_{salah satu} seperti yang ditunjukkan gambar. Resistensi udara tidak diperhitungkan. Gerakan ini dapat diperlakukan sebagai dua gerakan independen dan simultan: satu horizontal dengan konstan dan kecepatan vertikal lainnya di bawah aksi gravitasi.

x (t) = x_{salah satu} +v_sapi.T

dan (t) = y_{salah satu} +v_Oy.T -½g.T²

Persamaan ini adalah Persamaan Parametrik peluncuran proyektil. Seperti dijelaskan di atas, mereka memiliki parameter umum T, apa itu waktu.

Di segitiga sosok kanan berikut ini dapat dilihat:

v_sapi = v_{salah satu} cos θ_yo

v_Oy = v_{salah satu} dosa θ_yo

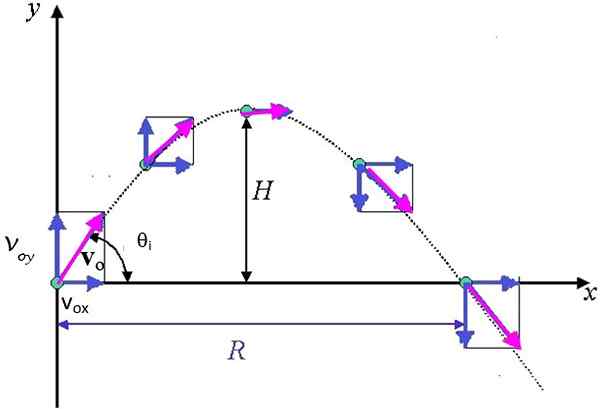Gambar 3. Lintasan parabola diikuti oleh proyektil, yang menunjukkan komponen vektor kecepatan. H adalah maksimum dan tinggi R adalah jangkauan horizontal maksimum. Sumber: AYUSH12GUPTA [CC BY-SA 4.0 (https: // createveCommons.Org/lisensi/by-sa/4.0)]

Dengan mengganti persamaan ini yang berisi sudut peluncuran dalam persamaan parametrik itu:

Dapat melayani Anda: difraksi suara: apa itu, contoh, aplikasi

x (t) = x_{salah satu} +v_{salah satu} cos θ_yo.T

dan (t) = y_{salah satu} +v_{salah satu}. dosa θ_yo.T -½g.T²

Persamaan Lintasan Parabola

Persamaan eksplisit lintasan adalah membersihkan T dari persamaan untuk x (t) dan mengganti dalam persamaan y (t) (t). Untuk memfasilitasi pekerjaan aljabar, dapat diasumsikan bahwa asal (0,0) berada pada titik peluncuran dan dengan cara ini x_{salah satu} = y_{salah satu} = 0.

Setelah menyederhanakan parameter "T“Itu telah dihilangkan dan persamaan yang tersisa adalah dan tergantung pada x: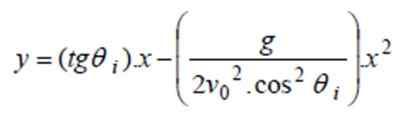

Ini adalah persamaan lintasan di Bentuk eksplisit.

Lintasan melingkar

Lintasan melingkar diberikan oleh:

(X - x_{salah satu})² + (dan dan_{salah satu})² = R²

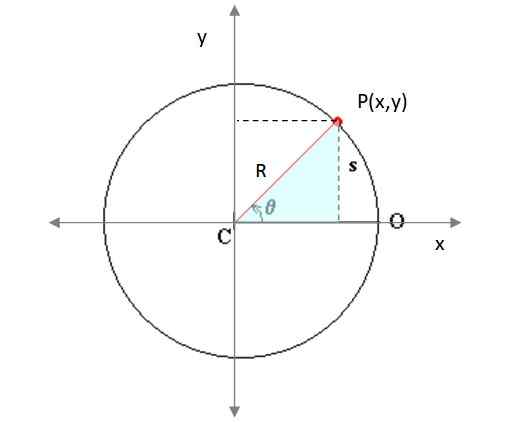Gambar 4. Partikel bergerak dalam lintasan melingkar di bidang. Sumber: dimodifikasi oleh f. Sepatu Wikimedia Commons.

Di sini x_{salah satu} dan dan_{salah satu} Mereka mewakili pusat keliling yang dijelaskan oleh ponsel dan r adalah jari -jari yang sama. P (x, y) adalah titik lintasan. Dari segitiga persegi panjang teduh (Gambar 3) diperingatkan bahwa:

x = r. cos θ

y = r. dosa θ

Parameter, dalam hal ini, adalah sudut sapuan θ, disebut perpindahan sudut. Dalam kasus tertentu bahwa kecepatan sudut Ω (sudut disapu per unit waktu) adalah konstan, dapat ditegaskan bahwa:

θ = θ_{salah satu} + ΩT

Dimana θ_{salah satu} Ini adalah posisi sudut awal partikel, yang jika diambil sebagai 0, dikurangi menjadi:

θ = ΩT

Dalam hal ini, waktu kembali ke persamaan parametrik seperti:

x = r.cos ΩT

y = r. sin ΩT

Vektor unit yo Dan J Mereka sangat nyaman untuk menulis fungsi posisi suatu objek R (T). Mereka menunjukkan arah pada sumbu X dan pada poros Dan masing -masing. Dalam istilahnya, posisi partikel yang menggambarkan gerakan melingkar yang seragam adalah:

R (t) = r.cos ΩT yo + R. sin ΩT J

Latihan terpecahkan

Latihan diselesaikan 1

Meriam dapat menembakkan peluru dengan kecepatan 200 m/s dan sudut 40º sehubungan dengan horizontal. Jika peluncuran dilakukan di medan datar dan perlawanan udara dihina, temukan:

a) Persamaan lintasan dan (x) ..

b) persamaan parametrik x (t) Dan dan T).

c) Jangkauan horizontal dan waktu proyektil berlangsung di udara.

d) Tinggi di mana proyektil terletak ketika x = 12.000 m

Solusi untuk)

a) Untuk menemukan lintasan, nilai -nilai yang diberikan dalam persamaan y (x) dari bagian sebelumnya diganti:

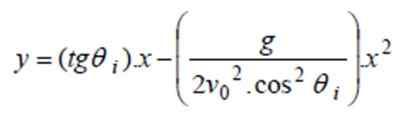
dan (x) = TG 40º. X - 9.8/(2 '400². cos²40º) X² ⇒  dan (x) = 0.8391 x - 0.0000522x²

Solusi b)

b) Titik peluncuran dipilih pada asal sistem koordinat (0,0):

x (t) = x_{salah satu} +v_sapi.T = 400'Cos 40º.T = 306.42. T.

dan (t) = y_{salah satu} +v_Oy.T -½g.T²= 400 'Sen 40º.T - 0.5 '9.8'T²= 257.12 t - 4.9.T²

Solusi C)

c) Untuk menemukan waktu proyektil berlangsung di udara, selesai dan (t) = 0, Menjadi peluncuran dilakukan di medan datar:

Dapat melayani Anda: apa itu kekasaran relatif dan absolut?

0 = 257.12.T - 4.9.T²

T = 257.12/4.9 s = 52.473 s

Lingkup maksimum horizontal mengganti nilai ini x (t):

X_Max = 306.42'52.47 m = 16077.7 m

Cara lain untuk menemukan x_Max Itu langsung melakukan y = 0 dalam persamaan lintasan:

0 = 0.8391 x_Max - 0.0000522 x²_Max

x = 0.8391 /0.0000522 m = 16078.5m

Ada perbedaan kecil karena pembulatan desimal.

D) Solusi

d) Untuk mengetahui ketinggian ketika x = 12000 m nilai ini diganti langsung dalam persamaan lintasan:

dan (12000) = 0.8391'12000 - 0.0000522'12000² M = 2552.4 m

Latihan diselesaikan 2

Fungsi posisi suatu objek diberikan oleh:

R (t) = 3t yo + (4 -5t²) J M

Menemukan:

a) Persamaan untuk lintasan. Kurva apa itu?

b) posisi awal dan posisi saat t = 2 detik.

c) perpindahan yang dilakukan setelah t = 2 detik.

Larutan

a) Fungsi posisi telah diberikan dalam hal vektor unit yo Dan J, yang masing -masing menentukan alamat pada sumbu X Dan Dan, Karena itu:

x (t) = 3t

dan T) = 4 -5t²

Persamaan lintasan dan (x) Dia sedang membersihkan T dari x (t) dan mengganti dan T):

T = x/3

dan (x) = 4 -5. (x/3)² = 4 - 5x²/9 (perumpamaan)

b) Posisi awal adalah: R (2) = 4 J M ; Posisi masuk T = 2 detik adalah R (2) = 6 yo -16 J M

c) perpindahan DR Ini adalah pengurangan dari dua vektor posisi:

ΔR = R (2) - R (2) = 6 yo -16 J- 4 J = 6 yo - dua puluh J M

Latihan diselesaikan 3

Bumi memiliki jari -jari r = 6300 km dan diketahui bahwa periode rotasi gerakannya di sekitar porosnya adalah suatu hari nanti. Menemukan:

a) Persamaan lintasan titik di permukaan bumi dan fungsi posisinya.

b) kecepatan dan percepatan titik tersebut.

Solusi untuk)

a) Fungsi posisi untuk titik mana pun di orbit melingkar adalah:

R (t) = r.cos ΩT yo + R.sin ΩT J

Anda memiliki jari -jari Bumi R, tetapi bukan kecepatan sudut Ω, namun dapat dihitung dari periode tersebut, mengetahui bahwa untuk gerakan melingkar, valid untuk mengatakan bahwa:

Ω = 2π × Frekuensi = 2π / periode

Periode pergerakan adalah: 1 hari = 24 jam = 1440 menit = 86400 detik, oleh karena itu: oleh karena itu:

Ω =  2π / 86400 s = 0.000023148 ​​s^-1

Mengganti fungsi posisi:

R (t) = r.cos ΩT yo + R. sin ΩT J = 6300 (cos 0.000023148t yo + Dosa 0.000023148t J) Km

Jalur dalam bentuk parametrik adalah:

x (t) = 6300. cos 0.000023148t

dan (t) = 6300. Dosa 0.000023148t

Solusi b)

b) Untuk gerakan melingkar, besarnya kecepatan linier v titik terkait dengan kecepatan sudut W melalui:

v = ΩR = 0.000023148 ​​s^-1'6300 km = 0.1458 km/s = 145.8 m/s

Bahkan menjadi gerakan yang konstan 145.8 m/s, Ada akselerasi yang menunjuk ke pusat orbit melingkar, bertanggung jawab untuk menjaga titik tetap pada rotasi. Itu adalah percepatan sentripetal ke_C, diberikan oleh:

ke_C = v² / R = (145.8 m/s)² / 6300 × 10³ m = 0.00337 m/s².

Referensi

1. Giancoli, d. Fisika. (2006). Prinsip dengan aplikasi. 6^th Prentice Hall. 22-25.
2. Kirkpatrick, l. 2007. Fisika: Pandangan Dunia. 6^ta Edisi Singkat. Pembelajaran Cengage. 23 - 27.
3. Resnick, r. (1999). Fisik. Volume 1. Edisi ketiga dalam bahasa Spanyol. Meksiko. Perusahaan Editorial Kontinental S.KE. dari c.V. 21-22.
4. Rex, a. (2011). Dasar -dasar fisika. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Fisika Universitas dengan Fisika Modern. 14^th. Ed. Volume1. 50 - 53.
6. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7^ma. Edisi. Meksiko. Editor Pembelajaran Cengage. 23-25.
7. Serway, r., Vulle, c. (2011). Dasar -dasar fisika. 9^na Ed. Pembelajaran Cengage. 43 - 55.
8. Wilson, J. (2011). Fisika 10. Pendidikan Pearson. 133 - 149.