Segitiga sama kaki

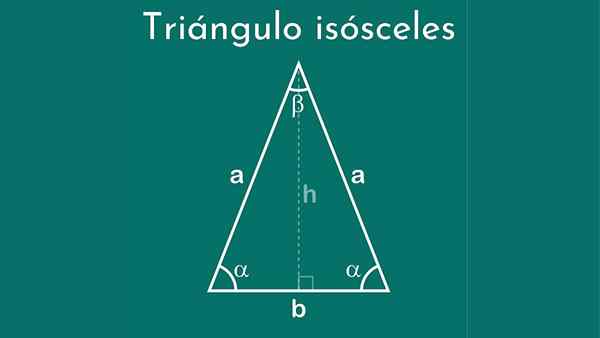
Segitiga Isosceles memiliki dua sisi yang sama dan satu berbeda

Apa itu Segitiga Isosceles?

A segitiga sama kaki Ini adalah poligon tiga sisi, di mana dua dari mereka memiliki ukuran yang sama dan sisi ketiga ukuran yang berbeda. Sisi terakhir ini disebut dasar. Karena karakteristik ini nama ini diberikan, yang dalam bahasa Yunani berarti "kaki yang sama".

Segitiga adalah poligon dianggap sebagai yang paling sederhana dalam geometri, karena mereka dibentuk oleh tiga sisi, tiga sudut dan tiga simpul. Mereka adalah orang -orang yang memiliki sedikit sisi dan sudut sehubungan dengan poligon lainnya, namun penggunaannya sangat luas.

Karakteristik Segitiga Isosceles

Segitiga Isosceles diklasifikasikan menggunakan ukuran sisinya sebagai parameter, karena dua sisinya kongruen, yaitu, mereka memiliki panjang yang sama.

Menurut amplitudo sudut internal, segitiga isosceles diklasifikasikan sebagai:

• Segitiga persegi panjang Isosceles: Dua sisinya sama. Salah satu sudutnya lurus (90^{salah satu}) Dan yang lainnya sama (45^{salah satu} setiap)
• Segitiga tumpul isosceles: Dua sisinya sama. Salah satu sudutnya tumpul (> 90^{salah satu}).
• Segitiga Acutangle Isosceles: Dua sisinya sama. Semua sudutnya akut (< 90^{salah satu}), Di mana dua memiliki ukuran yang sama.

Komponen

• Mediannya: Ini adalah garis yang pergi dari titik tengah di satu sisi dan mencapai titik yang berlawanan. Tiga media hadir pada titik yang disebut Baricentro atau Centroid.
• The Bisector: Ini adalah semi -right yang membagi sudut setiap titik menjadi dua sudut dengan ukuran yang sama. Itulah mengapa ia dikenal sebagai sumbu simetri, dan jenis segitiga ini hanya memiliki satu.
• Mediatrix: Ini adalah segmen tegak lurus terhadap sisi segitiga, yang berasal dari tengah ini. Ada tiga mediatik dalam segitiga dan menghadiri titik yang disebut circumcentro.
• Tinggi: Ini adalah garis yang bergerak dari simpul ke sisi yang berlawanan dan juga garis ini tegak lurus ke sisi itu. Semua segitiga memiliki tiga ketinggian, yang bertepatan pada titik yang disebut ortocenter.

Properti Segitiga Isosceles

Segitiga Isosceles didefinisikan atau diidentifikasi karena mereka memiliki beberapa sifat yang mewakili mereka, berasal dari teorema yang diusulkan oleh ahli matematika hebat:

Sudut internal

Jumlah sudut internal selalu sama dengan 180^{salah satu}.

Jumlah sisi

Jumlah ukuran dua sisi harus selalu lebih besar dari ukuran sisi ketiga, a + b> c.

Sisi kongruen

Segitiga Isosceles memiliki dua sisi dengan ukuran atau panjang yang sama; yaitu, mereka kongruen, dan sisi ketiga berbeda dari ini.

Sudut yang kongruen

Segitiga Isosceles juga dikenal sebagai segitiga isoangulous, karena mereka memiliki dua sudut yang memiliki ukuran yang sama (kongruen). Ini terletak di dasar segitiga, bertentangan dengan sisi yang memiliki panjang yang sama.

Dapat melayani Anda: prisma trapesium

Karena itu, teorema yang menetapkan itu:

"Jika segitiga memiliki dua sisi kongruen, sudut yang menentang pihak -pihak itu juga akan kongruen". Oleh karena itu, jika segitiga adalah Isosceles, sudut pangkalannya adalah kongruen.

Contoh:

Pada gambar berikut, segitiga ABC diamati. Saat menggambar bisectornya dari titik sudut B ke pangkalan, segitiga dibagi menjadi dua segitiga BDA dan BDC:

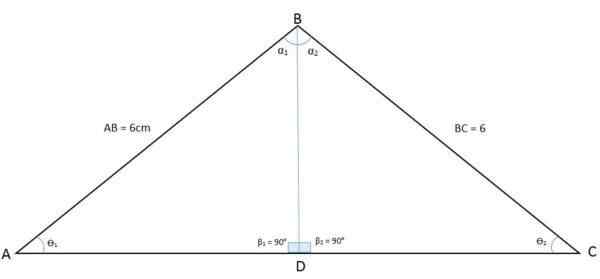Bisector yang membelah menjadi dua segitiga yang sama dengan segitiga suasana

Dengan cara ini, sudut Vertex B juga dibagi menjadi dua sudut yang sama. Bistor sekarang menjadi sisi umum (BD) antara dua segitiga baru, sedangkan sisi AB dan BC adalah sisi kongruen. Ini adalah kasus sisi, sudut, sisi (lal).

Itu menunjukkan bahwa sudut simpul A dan C memiliki ukuran yang sama, serta dapat ditunjukkan bahwa karena segitiga BDA dan BDC kongruen, sisi AD dan DC juga merupakan.

Tinggi, median, mediatrix dan bisector adalah kebetulan

Garis yang ditarik dari simpul yang berlawanan dengan pangkalan ke titik tengah dasar segitiga isosceles, pada saat yang sama tinggi, median dan mediatrix, serta bisektor relatif terhadap sudut yang berlawanan dari pangkalan.

Semua segmen ini bertepatan dalam yang mewakili mereka.

Contoh:

Pada gambar berikut ini segitiga ABC diamati dengan titik M medium yang membagi basis menjadi dua segmen BM dan CM.

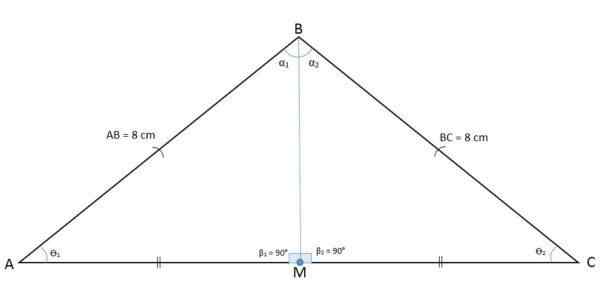Tinggi, median, mediatrix dan bisector adalah kebetulan

Saat menggambar segmen dari titik M ke titik berlawanan, menurut definisi median AM diperoleh, yang relatif terhadap simpul A dan ke sisi BC.

Karena segmen AM membagi segitiga ABC menjadi dua segitiga yang sama AMB dan AMC, itu berarti bahwa kasus sisi, sudut, sisi, dan oleh karena itu AM juga akan menjadi bisector Bâc.

Itulah sebabnya bisector akan selalu sama dengan median dan sebaliknya.

Segmen AM membentuk sudut yang memiliki ukuran yang sama untuk segitiga AMB dan AMC; Artinya, mereka tambahan, sehingga ukuran masing -masing adalah:

Med. (Amb) + med. (AMC) = 180^{salah satu}

2 _* Med. (AMC) = 180^{salah satu}

Med. (AMC) = 180^{salah satu} ÷ 2

Med. (AMC) = 90^{salah satu}

Dapat diketahui bahwa sudut yang dibentuk oleh segmen AM mengenai dasar segitiga lurus, menunjukkan bahwa segmen ini benar -benar tegak lurus terhadap pangkalan.

Oleh karena itu mewakili ketinggian dan mediatrix, mengetahui bahwa m adalah titik tengah.

Oleh karena itu, garis AM:

• Mewakili ketinggian bc.
• Adalah ukuran sedang.
• Itu terkandung dalam mediatrix BC.
• Itu adalah bisector dari sudut titik â

Ketinggian relatif

Ketinggian yang relatif terhadap sisi yang sama memiliki ukuran yang sama juga.

Dapat melayani Anda: angka sempurna: cara mengidentifikasi mereka dan contoh

Karena segitiga Isosceles memiliki dua sisi yang sama, dua ketinggiannya juga akan sama.

Orocentro, Baricentro, Incentro dan Colecentro Coinsides

Karena ketinggian, median, bisector, dan mediatrix yang terkait dengan pangkalan diwakili pada saat yang sama oleh segmen yang sama, orthocenter, baricentro, insentre dan circumcentro akan menjadi titik kolineal, yaitu, mereka akan ditemukan di baris yang sama:

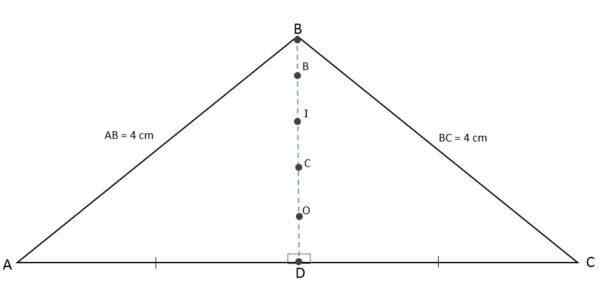Ortocenter, Baricentro, Incentro dan Circumcentro juga kebetulan

Perhitungan segitiga Isosceles

Cara menghitung perimeter?

Perimeter poligon dihitung dengan jumlah sisi.

Seperti dalam hal ini segitiga samaan memiliki dua sisi dengan ukuran yang sama, perimeternya dihitung dengan rumus berikut:

P = 2_*(sisi a) + (sisi b).

Cara menghitung ketinggian?

Ketinggian adalah garis tegak lurus dengan pangkalan, membagi segitiga menjadi dua bagian yang sama dengan memanjang ke titik berlawanan.

Ketinggian mewakili cateto yang berlawanan (a), setengah dari alas (b/2) ke cateto yang berdekatan dan sisi “a” mewakili hipotenuse yang di -hipoten.

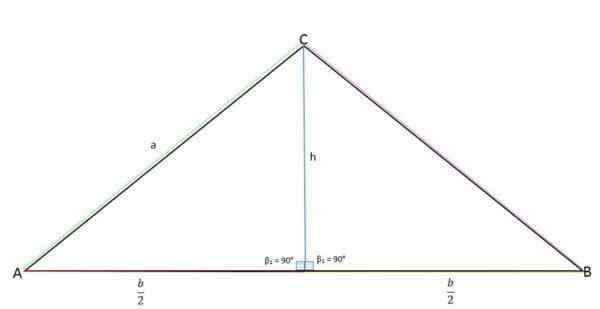Perhitungan ketinggian segitiga isosceles

Menggunakan teorema Pythagoras, nilai ketinggian dapat ditentukan:

ke² + B² = C²

Di mana:

ke² = Tinggi (h).

B² = B / 2.

C² = Sisi a.

Mengganti nilai -nilai itu dalam teorema Pythagoras, dan membersihkan ketinggian yang Anda miliki:

H² + (B / 2)² = ke²

H² + B² / 4 = ke²

H² = ke² - B² / 4

H = √ (ke² - B² / 4).

Jika sudut yang dibentuk oleh sisi kongruen diketahui, ketinggian dapat dihitung dengan rumus berikut:

Cara menghitung area tersebut?

Segitiga selalu dihitung dengan rumus yang sama, mengalikan pangkalan dengan tinggi dan membaginya dengan 2:

Ada kasus di mana hanya ukuran dua sisi segitiga yang diketahui dan sudut yang terbentuk di antara mereka. Dalam hal ini, untuk menentukan area yang perlu untuk menerapkan alasan trigonometri:

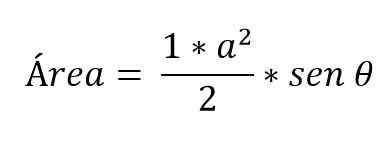
Cara menghitung dasar segitiga?

Karena segitiga Isosceles memiliki dua sisi yang sama, untuk menentukan nilai pangkalannya, perlu untuk mengetahui setidaknya ukuran ketinggian atau salah satu sudutnya.

Mengetahui tinggi, teorema Pythagoras digunakan:

ke² + B² = c²

Di mana:

ke² = Tinggi (h).

C² = Sisi a.

B² = B / 2, tidak diketahui.

Kami membersihkan b² dari formula dan kami harus:

B² = a² - C²

B = √ a² - C²

Karena nilai ini sesuai dengan setengah dari pangkalan, itu harus dikalikan dengan 2 untuk mendapatkan ukuran lengkap dari basis segitiga samaan:

B = 2 _* (√ a² - C²)

Dalam hal bahwa hanya nilai sisi yang sama dan sudutnya di antara mereka diketahui, trigonometri diterapkan, menarik garis dari simpul ke pangkalan yang membagi segitiga sama dengan dua segitiga persegi panjang.

Dengan cara ini, setengah dari pangkalan dihitung dengan:

Nilai tinggi dan sudut titik yang bertentangan dengan pangkalan juga diketahui. Dalam hal ini, dengan trigonometri dasar dapat ditentukan:

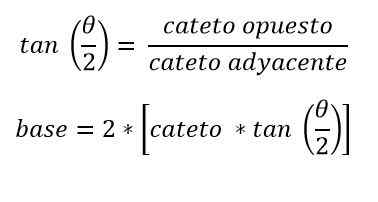
Latihan

Latihan Pertama

Temukan area Segitiga ABC Isosceles, mengetahui bahwa dua sisinya berukuran 10 cm dan sisi ketiga berukuran 12 cm.

Itu dapat melayani Anda: antiderivatif: rumus dan persamaan, contoh, latihan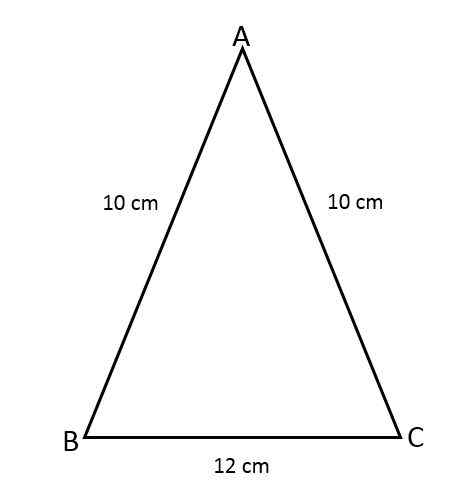

Larutan

Untuk menemukan area segitiga, itu perlu.

Data Segitiga Isosceles berikut tersedia:

• Sisi yang sama (a) = 10 cm.
• Dasar (b) = 12 cm.

Nilai diganti dalam rumus:

Latihan kedua

Panjang dua sisi yang sama dari segitiga isosceles berukuran 42 cm, penyatuan sisi -sisi ini membentuk sudut 130^{salah satu}. Tentukan nilai sisi ketiga, luas segitiga dan perimeter.

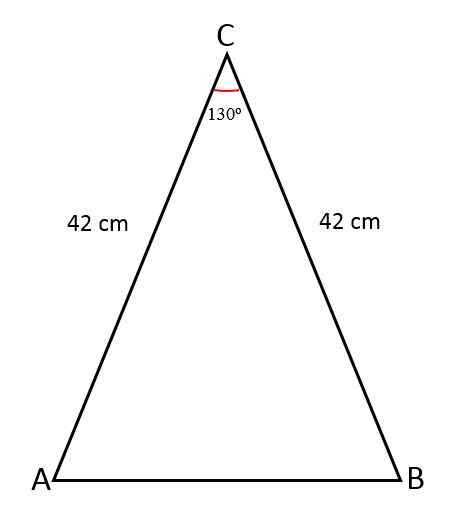
Larutan

Dalam hal ini, ukuran sisi dan sudut diketahui di antara ini.

Untuk mengetahui nilai sisi yang hilang, yaitu dasar segitiga itu, garis tegak lurus terhadapnya ditarik, membagi sudut menjadi dua bagian yang sama, satu untuk setiap segitiga persegi panjang yang terbentuk.

• Sisi yang sama (a) = 42 cm.
• Sudut (ɵ) = 130^{salah satu}

Sekarang, dengan trigonometri, nilai setengah dari basis dihitung, yang sesuai dengan setengah dari hipotenus:

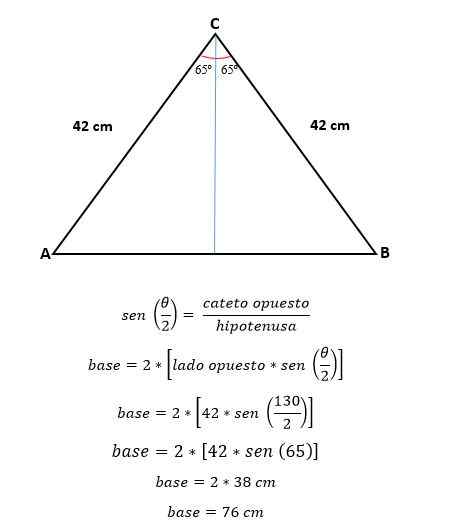
Untuk menghitung area, perlu untuk mengetahui ketinggian segitiga itu, yang dapat dihitung dengan trigonometri atau dengan teorema Pythagoras, sekarang nilai pangkalan sudah ditentukan.

Dengan trigonometri adalah:

Perimeter dihitung:

P = 2_*(sisi a) + (sisi b).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Latihan ketiga

Hitung sudut internal segitiga samaan, mengetahui bahwa sudut dasar adalah â = 55^{salah satu}

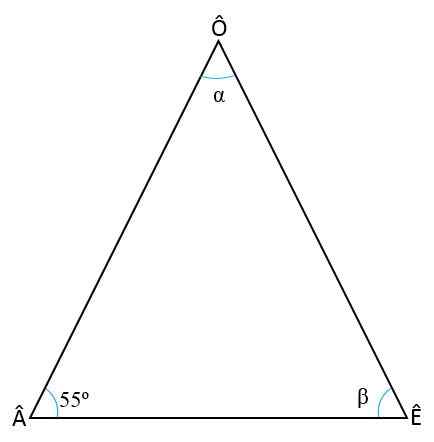
Larutan

Untuk menemukan dua sudut yang hilang (ê dan ô) perlu mengingat dua sifat segitiga:

• Jumlah sudut internal setiap segitiga akan selalu = 180^{salah satu}:

 + ê + ô = 180 ^{salah satu}

• Dalam segitiga Isosceles, sudut -sudut pangkalan selalu kongruen, yaitu, mereka memiliki ukuran yang sama, oleh karena itu: oleh karena itu:

 = ô

Ê = 55^{salah satu}

Untuk menentukan nilai sudut ê, nilai -nilai sudut lain dalam aturan pertama diganti dan ê dihapus:

55^{salah satu} + 55^{salah satu} + Ô = 180 ^{salah satu}

110 ^{salah satu} + Ô = 180 ^{salah satu}

Ô = 180 ^{salah satu} - 110 ^{salah satu}

Ô = 70 ^{salah satu}.

Referensi

1. Álvarez, e. (2003). Elemen Geometri: Dengan banyak latihan dan geometri kompas. Universitas Medellin.
2. Álvaro rendón, ke. R. (2004). Gambar Teknis: Buku catatan aktivitas.
3. Malaikat, a. R. (2007). Aljabar Dasar. Pendidikan Pearson.
4. Arthur Goodman, L. H. ( seribu sembilan ratus sembilan puluh enam). Aljabar dan trigonometri dengan geometri analitik. Pendidikan Pearson.
5. Baldor, a. (1941). Aljabar. Havana: Budaya.
6. José Jiménez, L. J. (2006). Matematika 2.
7. Tuma, J. (1998). Buku Pegangan Matematika Rekayasa. Wolfram Mathworld.