Sejarah Segitiga, Elemen, Klasifikasi, Properti

Itu segitiga Mereka adalah figur geometris datar dan tertutup, yang terdiri dari tiga sisi. Segitiga ditentukan oleh tiga garis yang dipotong dua hingga dua, dibentuk satu sama lain tiga sudut. Bentuk segitiga, penuh simbolisme, hadir dalam objek yang tak terhitung jumlahnya dan sebagai unsur konstruksi.

Asal usul segitiga hilang dalam sejarah. Dari bukti arkeologis diketahui bahwa kemanusiaan primitif mengenalnya dengan baik, karena sisa arkeologis mengkonfirmasi bahwa ia digunakan dalam alat dan senjata.

Gambar 1. segitiga. Sumber: Publik Domain Public.

Juga jelas bahwa orang Mesir kuno memiliki pengetahuan geometri yang kuat dan khususnya bentuk segitiga. Mereka diwujudkan dalam elemen arsitektur dari konstruksi monumental mereka.

Di Rhind Papyrus ada formula untuk perhitungan segitiga dan daerah trapeze, serta beberapa volume dan konsep trigonometri yang belum sempurna lainnya.

Di sisi lain, diketahui bahwa orang Babilonia dapat menghitung luas segitiga dan figur geometris lainnya, yang mereka gunakan untuk tujuan praktis, seperti divisi tanah. Mereka juga menyadari banyak sifat segitiga.

Namun, orang -orang Yunani kuno yang mensistematisasikan banyak konsep geometris yang sering terjadi saat ini, meskipun banyak dari pengetahuan itu tidak eksklusif, karena tentu saja dibagikan dengan peradaban kuno lainnya ini.

[TOC]

Elemen segitiga

Elemen segitiga apa pun ditunjukkan pada gambar berikut. Ada tiga: simpul, sisi dan sudut.

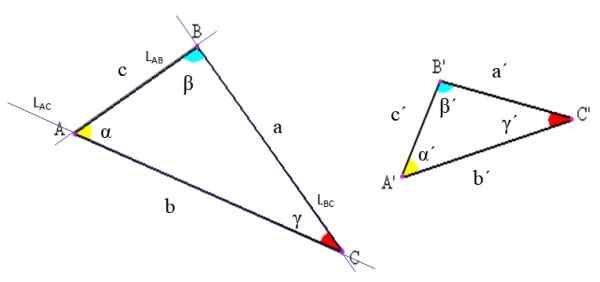Gambar 2. Notasi segitiga dan elemen mereka. Sumber: Wikimedia Commons, dimodifikasi oleh f. Zapata

-Sudut: Ini adalah titik persimpangan garis yang segmennya menentukan segitiga. Pada gambar atas misalnya, garis l_Ac yang berisi segmen AC, memotong garis l_AB yang berisi segmen AB tepat pada titik a.

-Sisi: Di antara setiap pasangan simpul segmen garis ditarik yang merupakan satu sisi segitiga. Segmen ini dapat dilambangkan dengan huruf -huruf ujungnya atau menggunakan surat tertentu untuk menyebutnya. Dalam contoh Gambar 2, sisi AB juga disebut "C".

-Sudut: Di antara masing -masing sisi dengan simpul umum, sudut berasal, yang simpulnya bertepatan dengan segitiga. Sudut umumnya dilambangkan dengan surat Yunani, seperti yang dinyatakan di awal.

Untuk membangun segitiga tertentu, dengan bentuk dan ukuran yang diberikan, hanya memiliki beberapa set data berikut:

-Ketiga sisi, cukup jelas dalam kasus segitiga.

-Dua sisi dan sudut di antara mereka, dan sisi yang tersisa segera ditarik.

-Dua sudut (internal) dan sisi di antara mereka. Dengan ekstensi, dua sisi yang hilang ditarik dan segitiga sudah siap.

Notasi

Umumnya dalam notasi segitiga konvensi berikut digunakan: simpul ditunjukkan dengan huruf kapital, sisi dengan huruf Latin kecil dan sudut oleh huruf Yunani (lihat Gambar 2).

Dengan cara ini segitiga dinamai sesuai dengan simpulnya. Misalnya, segitiga di sebelah kiri pada Gambar 2 adalah segitiga ABC, dan yang di sebelah kanan adalah segitiga a'b'c '.

Dimungkinkan juga untuk menggunakan notasi lain; Misalnya, sudut α pada Gambar 2 dilambangkan sebagai BAC. Perhatikan bahwa surat simpul berjalan di tengah dan huruf -huruf ditulis ke arah yang berlawanan dengan jarum jam.

Itu dapat melayani Anda: pembatasan masalah

Lain kali aksen sirkumflex ditempatkan untuk menunjukkan sudut:

Atau simbol ∠ digunakan, karena notasi sebelumnya mungkin tidak mudah dicetak, diikuti oleh huruf yang sesuai dengan simpul:

α = ∠A

Jenis segitiga

Ada beberapa kriteria klasifikasi segitiga. Yang paling umum adalah mengklasifikasikan mereka sesuai dengan ukuran sisi mereka atau sesuai dengan ukuran sudut mereka. Bergantung pada ukuran sisi mereka, segitiga bisa: skalen, isosceles atau ekuilateral:

-Sisi tak sama panjang: Tiga sisinya berbeda.

-Sama kaki: Memiliki dua sisi yang berbeda dan satu.

-Sama sisi: Ketiga sisinya sama.

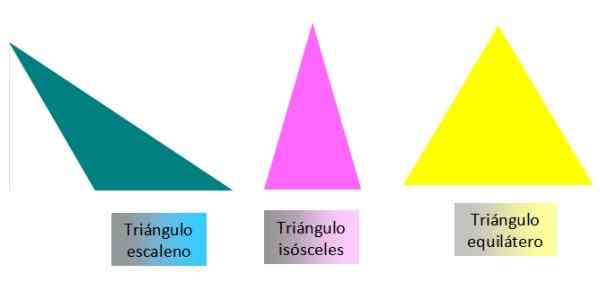Gambar 3. Klasifikasi segitiga di sisi mereka. Sumber: f. Zapata

Menurut ukuran sudut mereka, segitiga disebut seperti ini:

-Tumpul, Jika salah satu sudut internal lebih besar dari 90º.

-Acutangle, Ketika tiga sudut internal segitiga akut, yaitu, kurang dari 90º

-Persegi panjang, Jika salah satu sudut internalnya bernilai 90º. Sisi yang membentuk 90º disebut catetos dan sisi yang berlawanan dari sudut kanan adalah hipotenuse.

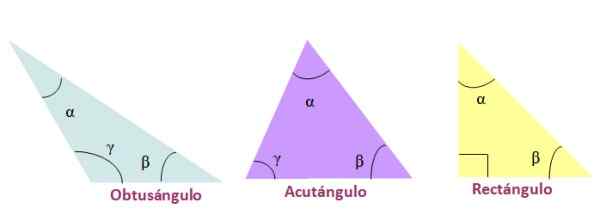Gambar 4. Klasifikasi segitiga dengan sudut internal mereka. Sumber: f. Zapata.

Kongruensi segitiga

Ketika dua segitiga memiliki bentuk yang sama dan berukuran sama, dikatakan bahwa mereka kongruen. Tentu saja kongruensinya terkait dengan kesetaraan, jadi mengapa dalam geometri kita berbicara tentang "dua segitiga kongruen" bukan "dua segitiga yang sama"?

Nah, lebih disukai menggunakan istilah "kongruensi" untuk tetap pada kebenaran, karena dua segitiga dapat memiliki bentuk dan ukuran yang sama, tetapi berorientasi berbeda di pesawat (lihat Gambar 3). Dari sudut pandang geometri, mereka tidak lagi sama.

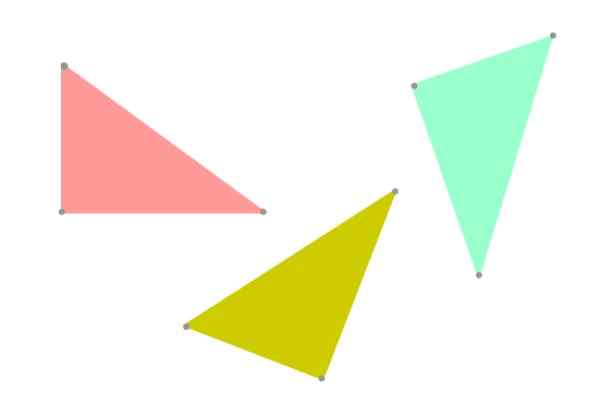Gambar 5. Segitiga kongruen, tetapi tidak harus sama, karena orientasinya di pesawat berbeda. Sumber: f. Zapata.

Kriteria Kongruensi

Dua segitiga kongruen jika ada dari situasi berikut yang terjadi:

-Tiga sisi mengukur sama (sekali lagi ini adalah yang paling jelas).

-Mereka memiliki dua sisi yang identik dan dengan sudut yang sama di antara mereka.

-Keduanya memiliki dua sudut internal yang identik dan sisi antara sudut ini adalah sama.

Seperti yang dapat dilihat, ini adalah tentang dua segitiga memenuhi kondisi yang diperlukan sehingga ketika membangunnya, bentuk dan ukurannya persis sama.

Kriteria kongruensi sangat berguna, karena dalam praktiknya, bagian -bagian dan komponen mekanis yang tak terhitung banyaknya harus diproduksi secara seri, sehingga tindakan dan bentuknya persis sama.

Kesamaan segitiga

Segitiga mirip dengan yang lain jika mereka memiliki bentuk yang sama, bahkan jika ukurannya berbeda. Untuk memastikan bahwa bentuknya sama, diperlukan bahwa sudut internal memiliki nilai yang sama dan bahwa sisinya proporsional.

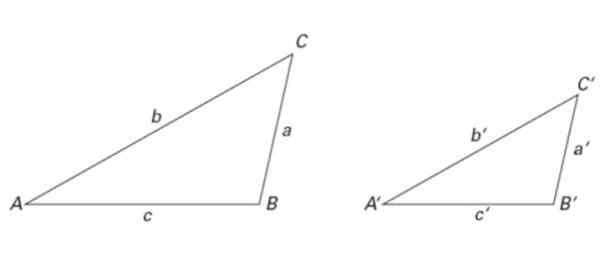Gambar 6. Dua segitiga serupa: ukurannya berbeda tetapi proporsinya sama. Sumber: f. Zapata.

Segitiga Gambar 2 juga serupa, serta yang ada pada Gambar 6. Dengan demikian:

∠ a = ∠ A ', ∠ B = ∠ B 'dan ∠ C = ∠ C '

Sedangkan untuk sisi, alasan berikut untuk kesamaan dipenuhi:

a/a '= b/b' = c/c '

Properti

Sifat dasar segitiga adalah sebagai berikut:

-Jumlah sudut internal segitiga selalu 180º.

-Untuk segitiga apa pun, jumlah sudut eksternalnya sama dengan 360 °.

Dapat melayani Anda: Penelitian Dasar: Karakteristik, Definisi, Contoh

- Sudut eksternal dari segitiga sama dengan jumlah dari dua sudut interior yang tidak berdekatan dengan sudut itu.

Teorema

Teorema pertama seperti itu

Mereka dikaitkan dengan filsuf Yunani dan matematikawan dari Miletus, yang mengembangkan beberapa teorema yang berkaitan dengan geometri. Yang pertama menetapkan yang berikut:

Jika beberapa garis paralel memotong dua garis transversal, mereka menentukan segmen yang proporsional.

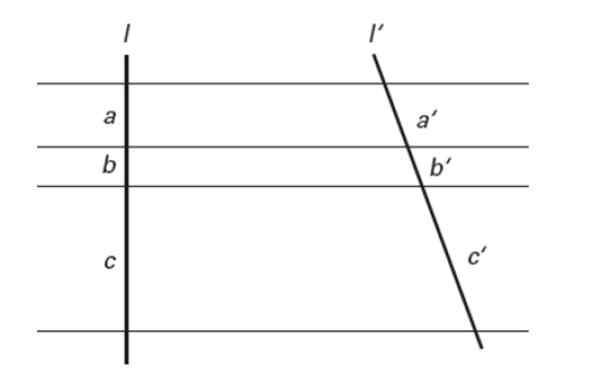Gambar 7. Teorema Tales. Sumber: f. Zapata.

Dengan kata lain:

a/a '= b/b' = c/c '

Teorema pertama dari demikian berlaku untuk segitiga, misalnya ada segitiga biru ABC di sebelah kiri, yang dipotong oleh paralel merah di sebelah kanan:

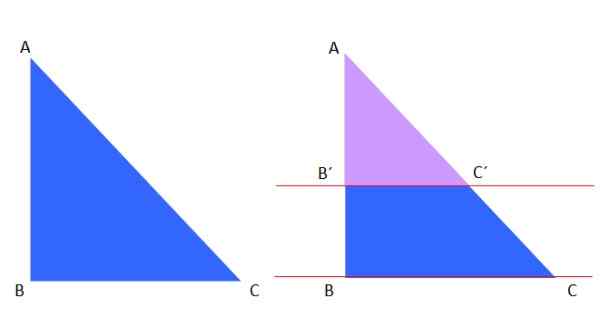Angka 8. Teorema segitiga yang sama dan serupa.

Segitiga Violet Violet mirip dengan ABC Blue Triangle, oleh karena itu, menurut teorema tersebut, berikut ini dapat ditulis:

Ab '/ac' = ab/ac

Dan itu konsisten dengan apa yang dijelaskan di atas di segmen kesamaan segitiga. Ngomong -ngomong, garis paralel juga bisa vertikal atau paralel dengan hipotenus dan segitiga serupa diperoleh.

Teorema kedua ini

Teorema ini juga mengacu pada segitiga dan lingkar tengah atau, seperti yang ditunjukkan di bawah ini. Dalam gambar ini, AC adalah diameter lingkar dan B adalah titiknya, menjadi B berbeda dari A dan B.

Teorema kedua menyatakan bahwa:

Sudut antara segmen AB dan BC selalu 90º, oleh karena itu ABC Triangle adalah persegi panjang.

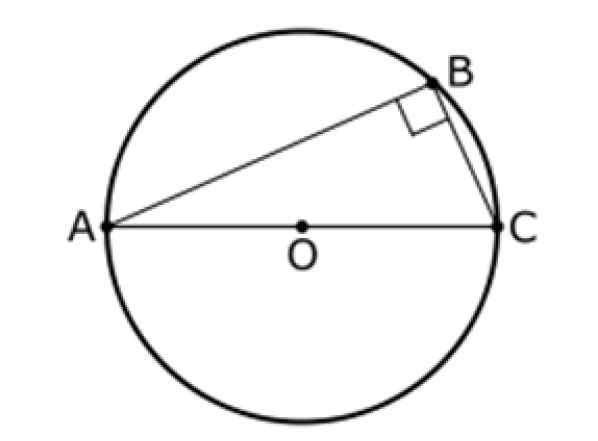Gambar 9. Teorema kedua seperti itu. Sumber: Wikimedia Commons. InductiveLoad [domain publik].

teorema Pythagoras

Ini adalah salah satu teorema paling terkenal dalam sejarah. Ini karena matematikawan Yunani Pythagoras dari Samos (569 - 475. C.) dan berlaku untuk segitiga kanan. Mengatakan begitu:

Jumlah kotak dari panjang kategori segitiga persegi panjang, sama dengan panjang hipotenus tinggi ke kotak.

Jika kita menganggap sebagai contoh segitiga biru Gambar 8, atau segitiga violet, karena keduanya adalah persegi panjang, maka dapat dikatakan bahwa:

Ac² = Ab² + Bc² (Segitiga Biru)

Ac '² = Ab '² + Bc '² (Segitiga Violet)

Luas segitiga

Area segitiga diberikan oleh produk pangkalannya ke dan tingginya H, dibagi dengan 2. Dan dengan trigonometri, ketinggian ini dapat ditulis sebagai H = b sinθ.

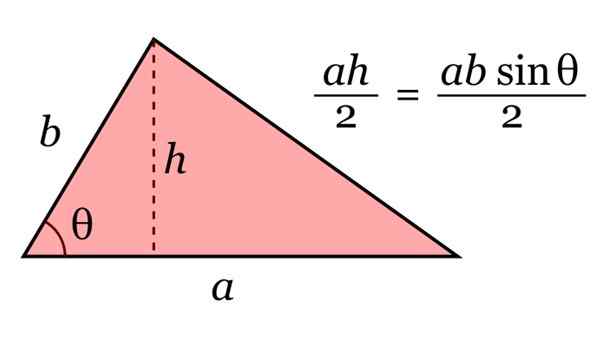Gambar 10. Area segitiga. Sumber: Wikimedia Commons.

Contoh segitiga

Contoh 1

Dikatakan bahwa melalui teorema pertamanya, seperti itu berhasil mengukur ketinggian piramida besar di Mesir, salah satu dari 7 keajaiban dunia kuno, mengukur bayangan yang diproyeksikan di tanah dan yang memproyeksikan saham yang terjebak di dalamnya tanah.

Ini adalah skema prosedur yang diikuti oleh seperti itu:

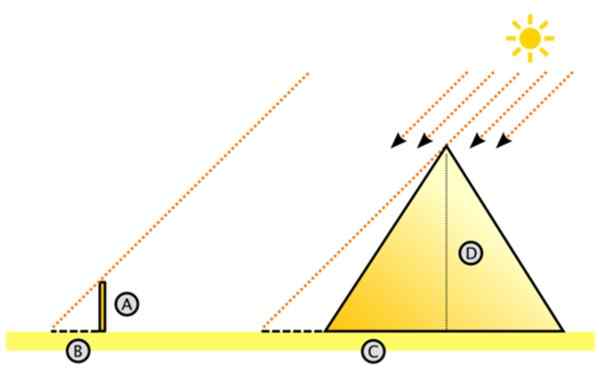Gambar 11. Skema untuk mengukur ketinggian piramida besar dengan kesamaan segitiga. Sumber: Wikimedia Commons. Dake [CC BY-SA 3.0 (http: // createveCommons.Org/lisensi/by-sa/3.0/]]

Sungguh benar bahwa sinar matahari mempengaruhi paralel. Dengan mengingat hal ini, dia membayangkan segitiga kanan kanan besar.

Ada ketinggian piramida dan C adalah jarak di tanah yang diukur dari pusat ke bayangan yang diproyeksikan oleh piramida di lantai gurun. Mungkin melelahkan untuk mengukur C, tetapi tentu saja lebih mudah daripada mengukur ketinggian piramida.

Di sebelah kiri adalah segitiga kecil, dari kucing A dan B, di mana A adalah ketinggian pasak yang terjebak secara vertikal di lantai dan B adalah bayangan yang diproyeksikannya. Kedua panjangnya dapat diukur, seperti C (C sama dengan panjang bayangan + setengah dari panjang piramida).

Dapat melayani Anda: apa itu rangsangan taktil?

Kemudian, dengan kesamaan segitiga:

A/b = d/c

Dan ketinggian piramida besar ternyata: d = c.(A/B)

Contoh 2

Armor konstruksi sipil adalah struktur berdasarkan batang kayu lurus tipis atau logam, yang digunakan sebagai dukungan di banyak bangunan. Mereka juga dikenal sebagai kisi, rangka atau reticulated (BRUSS dalam bahasa Inggris).

Di dalamnya segitiga selalu ada, karena batang saling berhubungan pada titik yang disebut node, yang mungkin diperbaiki atau diartikulasikan.

Gambar 12. Segitiga ada di bingkai jembatan ini. Sumber: Pxhere.

Contoh 3

Metode yang dikenal sebagai triangulasi memungkinkan Anda untuk mendapatkan lokasi titik yang tidak dapat diakses mengetahui jarak lain yang lebih mudah untuk diukur, dengan syarat bahwa segitiga terbentuk yang mencakup di antara simpulnya lokasi yang diinginkan.

Misalnya, dalam gambar berikut ini Anda ingin tahu pada titik mana laut adalah kapal, dilambangkan sebagai b.

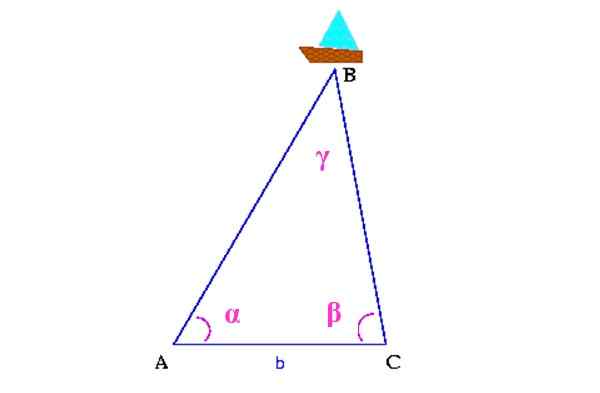Gambar 13. Skema triangulasi untuk menemukan kapal. Sumber: Wikimedia Commons. Colette [CC BY-SA 3.0 (http: // createveCommons.Org/lisensi/by-sa/3.0/]]

Pertama, jarak antara dua titik di pantai diukur, yang pada gambarnya adalah A dan C. Maka Anda harus menentukan sudut α dan β, dengan bantuan a teodolit, Perangkat yang berfungsi untuk mengukur sudut vertikal dan horizontal.

Dengan semua informasi ini, segitiga dibangun di atas simpul atasnya adalah kapalnya. Itu akan mengurangi sudut γ, dengan cara.

Latihan

Latihan 1

Pada gambar yang ditunjukkan, sinar matahari paralel. Dengan cara ini pohon tinggi 5 meter memproyeksikan bayangan 6 meter di tanah. Pada saat yang sama, bayangan bangunan adalah 40 meter. Mengikuti teorema seperti itu, temukan ketinggian bangunan.

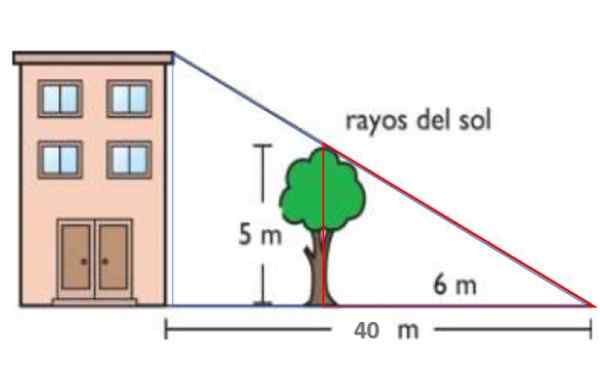Gambar 14. Skema untuk tahun ini diselesaikan 1. Sumber: f. Zapata.

Larutan

Segitiga merah memiliki sisi masing -masing 5 dan 6 meter, sedangkan biru memiliki ketinggian h - ketinggian bangunan dan dasar 40 meter. Kedua segitiga itu serupa, oleh karena itu:

H / 40 = 5/6 → H = 40.(5/6) m = 33.3 m

Latihan 2

Anda perlu mengetahui jarak horizontal antara dua titik KE Dan B, Tetapi mereka terletak di medan yang sangat tidak teratur.

Kira -kira di titik tengah (p_M) Dari tanah ini keunggulan 1 menonjol.Tinggi 75 meter. Jika pita pengukur menunjukkan panjang 26 meter yang diukur dari A ke menonjol, dan 27 meter dari B ke titik yang sama, temukan jarak AB.

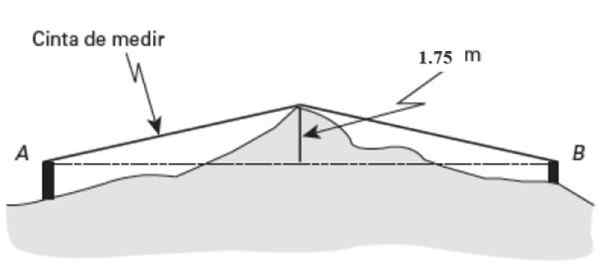Gambar 15. Skema untuk latihan diselesaikan 2. Sumber: Jiménez, R. Matematika II. Geometri dan Trigonometri.

Larutan

Teorema Pythagoras diterapkan pada salah satu dari dua segitiga persegi panjang pada gambar. Dimulai dengan yang di sebelah kiri:

Hypotenuse = c = 26 meter

Tinggi = a = 1.75 meter

Ap_M = (26² - 1.75²)^1/2 = 25.94 m

Sekarang Pythagoras diterapkan di segitiga kanan, kali ini c = 27 meter, a = 1.75 meter. Dengan nilai -nilai ini:

Bp_M= (27² - 1.75²)^1/2 = 26.94 m

Jarak AB menambahkan hasil ini:

AB = 25.94 m +26.94 m = 52.88 m.

Referensi

1. Baldor, j. KE. 1973.Geometri datar dan ruang. Budaya Amerika Tengah.
2. Barredo, d. Geometri segitiga. Pulih dari: ficus.pntic.MEC.adalah.
3. Jiménez, r. 2010. Matematika II. Geometri dan Trigonometri. Edisi kedua. Pearson.
4. Wentworth, g. Geometri planet. Pulih dari: Gutenberg.org.
5. Wikipedia. Segi tiga. Pulih dari: is. Wikipedia.org.