Trinomial persegi yang sempurna

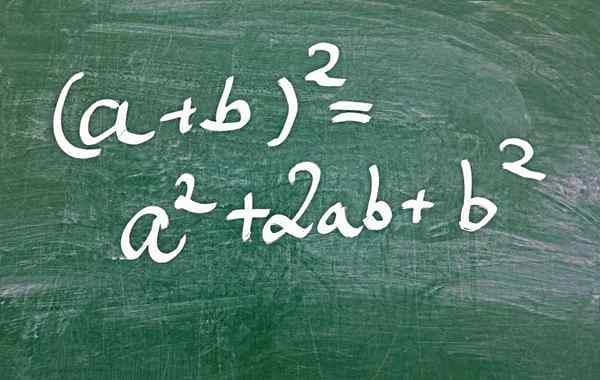Gambar 1.- Salah satu cara untuk mendapatkan trinomial persegi yang sempurna adalah melalui kuadrat dari jumlah

Apa trinomial persegi yang sempurna?

Trinomial persegi yang sempurna adalah bahwa polinomial dari tiga istilah, dua di antaranya merupakan kotak sempurna dari jumlah A dan B dan didahului dengan tanda yang sama, sedangkan istilah ketiga persis produk ganda A dan B, yang bisa dari tanda yang berbeda.

Trinomial persegi yang sempurna diperoleh dengan persegi jumlah atau perbedaan binomial dan secara aljabar, bentuknya adalah sebagai berikut:

ke² ± 2 ∙ ab + b²

Seperti yang dapat dilihat, trinomial persegi yang sempurna berisi:

• Dua istilah kuadratik non -serupa didahului dengan tanda yang sama: a² dan B²
• Istilah ketiga 2 ∙ ab, yang merupakan produk ganda dari akar kuadrat dari istilah kuadratik dan yang dapat didahului dengan tanda positif atau negatif.

Trinomial persegi yang sempurna bisa menjadi satu atau lebih variabel. Misalnya, trinomial berikut adalah kuadrat sempurna dari suatu variabel:

• X² + 6x + 9

Perhatikan bahwa istilah pertama (x²) dan ketiga (9) adalah persegi, masing -masing, dari jumlah yang disebut a dan b. Memang, x² Itu adalah kuadrat x dan 9 adalah kuadrat dari 3. Dengan cara ini Anda dapat menulis yang berikut:

a = x

B = 3

Dan istilah yang tersisa adalah produk ganda dari x dan 3:

6x = 2 ∙ 3 ​​∙ x

Setelah verifikasi dilakukan, dapat dipastikan bahwa trinomial ini sempurna persegi.

Contoh

Gambar 2.- Contoh trinomial persegi sempurna. Sumber: f. Zapata.

Trinomial persegi sempurna juga muncul dalam dua atau lebih variabel, misalnya:

4x² + 4xy + dan²

Ini adalah trinomial dalam dua variabel: "x" dan "y". Dapat yakin bahwa itu adalah trinomial persegi yang sempurna, karena menyajikan dua istilah kuadratik:

4x² = (2x)²

Dan² = (y)²

Dan istilah yang tersisa adalah produk ganda dari akar persegi masing -masing: "2x" dan "y":

Dapat melayani Anda: orthoedro: rumus, area, volume, diagonal, contoh

4xy = 2 ∙ 2x ∙ dan

Trinomial yang disajikan sejauh ini adalah grade 2 dalam variabel "x", tetapi mereka tidak harus seperti ini. Trinomial berikut adalah grade 4 di "X":

9x⁴ - 30x²YZ + 25Y²z²

Mudah diverifikasi bahwa ini adalah trinomial persegi yang sempurna. Istilah pertama adalah persegi 3x yang sempurna², Sejak (3x²)² = 9x⁴.

Istilah 25y²z² sama dengan (5yz)². Akhirnya, istilah yang tersisa adalah 2 ∙ 3x²∙ 5yz = 30 x²dan z.

Di sisi lain, trinomial yang ditunjukkan di bawah ini bukan trinomial persegi yang sempurna:

• X²  + 8x - 16

Ini bukan trinomial persegi yang sempurna karena 16, meskipun 4², Itu didahului oleh tanda negatif, sedangkan istilah kuadratik lainnya (x²) positif.

• X²  - 15x + 25

Juga bukan trinomial persegi yang sempurna, karena meskipun memiliki dua istilah kuadrat: x² dan 5², Istilah 15x tidak sama dengan 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Trinomial ini bukan kotak sempurna, karena hanya berisi istilah kuadratik: 4x² = (2x)².

Kuadrat dari jumlah dan kuadrat dari perbedaan

Trinomial persegi yang sempurna diperoleh dengan mengembangkan dua jenis produk terkenal:

• Kuadrat dari jumlah.
• Kuadrat perbedaan.

Pertama, pengembangan diperoleh dari properti distributif, karena menaikkan binomial persegi berarti mengalikannya dengan dirinya sendiri:

(A ± B)² = (a ± b) × (a ± b) = a² ± A ∙ B ± B ∙ A + B² = a² ± 2a ∙ b + b²

Trinomial yang diperoleh adalah hasil yang dihafal hanya dengan sedikit latihan dan merupakan semacam jalan pintas yang memfasilitasi pengembangan, itulah sebabnya disebut produk yang luar biasa.

Dapat melayani Anda: Angka transenden: Apa itu, formula, contoh, latihan

Trinomial berikut mudah diperoleh dengan produk terkenal, tanpa menampilkan properti distributif.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 dan² +20xy + 4x²

Faktorisasi trinomial persegi yang sempurna

Operasi yang sering dan perlu dalam aljabar adalah faktorisasi trinomial kuadrat sempurna, yang melaluinya trinomial dinyatakan sebagai kuadrat dari jumlah atau pengurangan dua istilah (binomial).

Ini adalah operasi terbalik untuk mengembangkan produk terkenal, karena memiliki trinomial yang dihasilkan, idenya adalah untuk mendapatkan binomial yang memunculkannya ketika naik ke 2.

Misalnya, dalam trinomial persegi 4x sempurna yang dianalisis sebelumnya² + 4xy + dan², Apa binomial yang saat dikuadratkan itu memunculkan Anda?

Akar kuadrat masing -masing istilah kuadrat adalah:

√ (4x²) = 2x

Yang setara dengan: 4x² = (2x)²

√ (dan²) = y

Setara dengan mengatakan itu: dan² = (y)²

Karena itu:

4x² + 4xy + dan² = (2x + y)²

Dan apa binomial yang berasal dari trinomial persegi yang sempurna⁴ - 30x²YZ + 25Y²z²? Sekali lagi akar kuadrat dari istilah kuadratik diekstraksi:

√ (9x⁴) = 3x²

√ (25 dan²z²) = 5yz

Jadi:

(3x² - 5yz)² = 9x⁴ - 30x²YZ + 25Y²z²

Latihan terpecahkan

Latihan 1

Dalam masing -masing trinomial berikut, selesaikan kosong dengan istilah yang hilang untuk menjadi trinomial persegi yang sempurna:

saya² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Solusi untuk

Menurut formula produk terkenal:

Dapat melayani Anda: sudut pelengkap: yang mana dan bagaimana mereka dihitung, contoh, latihan

(A ± B)² = A² ± 2a ∙ b + b²

Dari trinomial:

M² + 18m + _____

Itu mengikuti itu:

a = m (jadi itu² = m²)

Selain itu, istilah pusatnya adalah: 2 ∙ A ∙ B = 2M ∙ B = 18m, oleh karena itu b = 9 dan kuadratnya adalah 9² = 81. Guy by rumus produk terkenal, trinomial seperti ini:

(M + 9)² = M² + 18m + 81

• Solusi b

Dalam trinomial ini:

4x² - _____ + 64

Anda bisa tahu dan B:

A = √ (4x²) = 2x

B = √64 = 8

Oleh karena itu, istilah yang hilang adalah produk ganda dari A dan B:

2 ∙ ab = 2 ∙ 8 ∙ 2x = 32x

Dan trinomial yang dicari adalah:

4x² - 32x + 64

• Solusi c

Di trinomial:

_____ + 30n + 25

Istilah pertama hilang, tetapi diketahui bahwa:

B = √25 = 5

DAN

2 ∙ ab = 2 ∙ a ∙ 5 = 10a = 30n

Oleh karena itu a = 3n dan trinomial yang dicari adalah:

9n² + 30n + 25

Latihan 2

Periksa apakah yang berikutnya adalah trinomial persegi yang sempurna dan faktornya:

16y² - 24yz + 9z²

• Larutan

Pertama terbukti bahwa istilah kuadratik didahului dengan tanda yang sama dan kemudian akar persegi masing -masing ditemukan:

A = √ (16y²) = 4y

B = √ (9z²) = 3z

Maka Anda harus memverifikasi apakah istilah yang tersisa adalah produk ganda dari A dan B:

2 ∙ ab = 2 ∙ 4y ∙ 3z = 24yz

Jika ya, maka trinomial dapat menjadi faktor sebagai kuadrat dari perbedaan, karena istilah pusat didahului dengan tanda negatif:

16y² - 24yz + 9z² = (4y - 3z)²

Referensi

1. Jiménez, r. 2008. Aljabar. Prentice Hall.
2. Pelajaran Matematika Kate. Trinomial persegi yang sempurna. Pulih dari: Katesmathlessons.com.
3. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
4. Zill, d. 2008. Prekcculment dengan kemajuan perhitungan. 4. Edisi. Bukit McGraw.