Kami menjelaskan apa dan apa saja langkah -langkah dispersi, dan kami memberikan beberapa contoh

Apa itu langkah -langkah dispersi?

Itu Ukuran dispersi atau variasi, dalam statistik, mengukur seberapa banyak distribusi data dari nilai ukuran pusat bergerak, seperti rata -rata atau rata -rata aritmatika. Nilainya selalu positif dan biasanya berbeda dari 0, kecuali dalam kasus data yang identik.

Jika ukuran dispersi menghasilkan nilai kecil, itu berarti bahwa data terletak sangat dekat dengan rata -rata, tetapi jika itu besar, itu berarti bahwa data lebih tersebar, oleh karena itu, jauh dari rata -rata.

Langkah -langkah dispersi sangat penting dari sudut pandang statistik, tidak hanya sebagai indikator aritmatika variasi data, tetapi sebagai bantuan yang sangat berharga ketika Anda ingin meningkatkan kualitas, baik dalam pembuatan produk maupun dalam penyediaan layanan.

Contohnya adalah jajaran perhatian di bank. Waktu rata -rata menunda pelanggan ketika mereka membuat baris yang unik dan kemudian didistribusikan di box office, sama seperti jika mereka membuat garis individu di depan masing -masing.

Namun, dispersi lebih rendah pada baris tunggal, yang berarti waktu perhatian individu sangat mirip dengan masing -masing klien. Pelanggan telah menyatakan bahwa mereka merasa lebih nyaman dengan cara ini, bahkan jika waktu perawatan rata -rata sama di kedua modalitas.

Langkah -langkah dispersi utama

Yang utama adalah: peringkat, varians, standar deviasi dan koefisien variasi.

Jangkauan

Peringkat r dari set data didefinisikan pada perbedaan antara nilai maksimum x_Max dan nilai minimum x_Min dari keseluruhan:

Rang = r = nilai maksimum - nilai minimum = x_Max - X_Min

Dapat melayani Anda: berapa angka? 8 Penggunaan Utama

Rentang ini cepat menghitung, tetapi sangat sensitif terhadap nilai -nilai ekstrem, dan memiliki kelemahan karena tidak mempertimbangkan nilai -nilai perantara. Oleh karena itu, ini hanya digunakan untuk memiliki ide awal, perkiraan dispersi data.

Contoh peringkat

Ini adalah daftar jumlah badai di Atlantik selama 14 tahun terakhir:

8; 9; 7; 8; limabelas; 9; 6; 5; 8; 4; 12; 7; 8; 2

Data nilai maksimum adalah 15, dan nilai minimum adalah 2, oleh karena itu: oleh karena itu:

R = nilai maksimum - nilai minimum = x_Max - X_Min = 15 - 2 = 13 badai

Perbedaan

Ukuran ini digunakan untuk membandingkan masing -masing data dengan rata -rata set, dan dihitung dengan menambahkan perbedaan, tinggi persegi, antara setiap nilai dengan rata -rata dan membagi dengan jumlah total nilai.

Menjadi:

-Rata -rata: μ

-Nilai apa pun, milik set data: x_yo

-Jumlah total pengamatan: n

Menunjukkan varian populasi seperti σ², Ekspresi untuk menghitungnya adalah:

Dan ketika sampel populasi diambil, lebih disukai untuk menghitung varian dengan cara ini:

Di mana varian sampel telah dilambangkan dengan S, dan rata -rata X dengan batang, untuk meninggalkan penggunaan huruf -huruf Yunani kepada populasi. Alasan untuk membagi antara N-1, bukan N, adalah untuk varian sampel untuk tidak meremehkan populasi, apa yang selalu terjadi ketika membelah antara n.

Di sisi lain, gagasan mengimbangi setiap perbedaan antara data dan rata -rata adalah untuk mencegah mereka menambahkannya 0, karena beberapa perbedaan akan positif dan negatif lainnya, yang cenderung membatalkan jumlah. Sebaliknya, kotak selalu positif.

Itu dapat melayani Anda: probabilitas frekuensi: konsep, bagaimana itu dihitung dan contoh

Oleh karena itu, varian selalu positif, bahkan jika perbedaan antara x_yo Dan rata -rata negatif, dan keuntungan utamanya dari varian adalah bahwa ia memperhitungkan setiap data dari set.

Tetapi ia memiliki ketidaknyamanan bahwa unit -unitnya tidak sama dengan data, misalnya, jika ini terdiri dari waktu, diukur dalam hitungan menit, varian set akan diberikan dalam hitungan menit ke kotak.

Contoh varian

Perhitungan varians membutuhkan penemuan rata -rata. Mengambil data angka badai, rata -rata dihitung oleh:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 Badai.Oleh karena itu, variannya adalah:

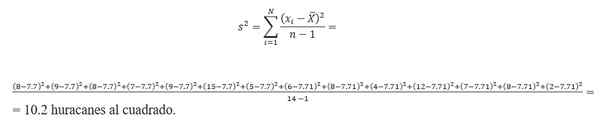
Deviasi standar

Untuk memperbaiki masalah kurangnya kesesuaian antara unit, standar deviasi didefinisikan σ, Seperti akar kuadrat dari varian:

Dan secara analog, dalam kasus sampel:

Ada aturan empiris untuk memperkirakan nilai standar deviasi set data sampel, berdasarkan rentang. Menurut aturan ini, standar deviasi adalah sekitar seperempat r:

S ≈ r/4

Ini memiliki keuntungan memungkinkan perkiraan cepat dari standar deviasi, karena operasi jauh lebih sederhana.

Deviasi standar adalah, dengan banyak, ukuran dispersi yang paling umum digunakan, sehingga layak untuk menyoroti karakteristik utamanya:

• Deviasi standar menunjukkan seberapa banyak data media bergerak
• Itu selalu positif, tetapi bisa 0 jika semua data identik
• Semakin besar nilai standar deviasi, semakin tersebar data
• Unit deviasi standar sama dengan variabel yang diteliti
• Nilainya berubah dengan cepat ketika salah satu data (atau lebih) memiliki nilai yang sangat berbeda dari yang lain
• Nilai standar deviasi bias, yaitu, rata -rata standar deviasi tidak didistribusikan di sekitar rata -rata, berbeda dengan varians, yang tidak berbasis -bias.

Dapat melayani Anda: Acutangle Triangle

Contoh standar deviasi

Melanjutkan dengan contoh badai, standar deviasi adalah:

Atau, jika lebih disukai menggunakan pendekatan standar deviasi melalui rentang, nilai yang cukup dekat diperoleh:

S = 13/4 = 3.25

Koefisien variasi

Koefisien variasi dilambangkan dengan inisial CV atau R, dalam beberapa teks, dan keduanya untuk populasi, dan untuk sampel, menghubungkan standar dan deviasi rata -rata, sebagai persentase:

O Nah:

Persamaannya valid selama rata -rata berbeda dari 0.

Sebagai aturan, koefisien variasi dibulatkan ke satu desimal, dan digunakan untuk membandingkan data dari dua populasi yang berbeda.

Contoh koefisien variasi

Waktu tunggu dalam hitungan detik, untuk klien bank, dicatat dalam dua situasi: ketika mereka membuat barisan yang unik dan ketika mereka membuat peringkat individu sebelum kantor tiket perhatian. Hasilnya adalah sebagai berikut:

Kedua set data dapat dibandingkan melalui koefisien variasi masing -masing:

Baris tunggal

• Rata -rata = 429 detik
• Deviasi = 28.6 detik
• CV = (28.6/429) x 100 = 6.7 %

Peringkat individu

• Rata -rata = 429 detik
• Deviasi = 109.3 detik
• CV = (109.3/429) x 100 = 25.5 %

Karena nilai terakhir ini lebih besar, ini menunjukkan bahwa ada lebih banyak variabilitas dalam waktu layanan pelanggan ketika mereka membuat peringkat individu daripada ketika mereka membuat baris yang unik, meskipun waktu rata -rata sama dalam setiap kasus.