Nilai mutlak

Berapa nilai absolut?

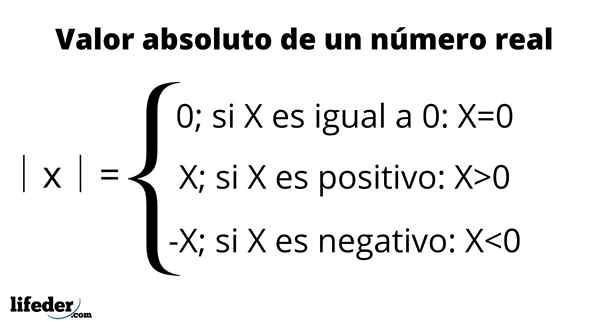
Dia nilai mutlak bilangan real didefinisikan sebagai jarak antara angka itu dan 0 dari garis nyata. Untuk menjadi jarak, nilainya selalu positif atau nol dan sama dengan angka angka.

Nilai absolut diwakili dengan menempatkan angka antara dua batang vertikal, simbol yang dibaca: "nilai absolut dari”, Seperti dirangkum dalam tabel berikut:

Misalnya, nilai absolut -3 ditulis sebagai │ -3│ dan sama dengan 3. Ini berarti bahwa antara -3 dan 0 ada tiga unit, yang mewakili angka -angka di garis nyata. Di sisi lain, nilai absolut +3 atau hanya 3, juga sama dengan 3, karena dengan mengukur jaraknya ke 0 juga tiga unit.

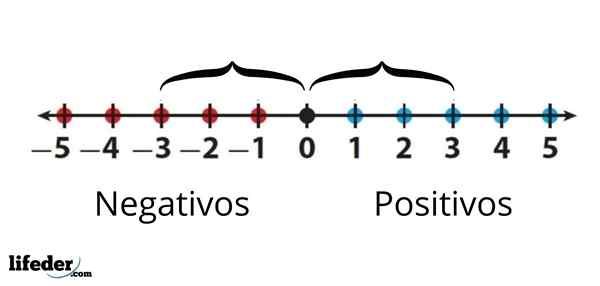Nilai absolut -3 sama dengan nilai absolut +3, karena jarak antara baik ke 0 adalah sama adalah sama

Singkatnya, nilai absolut dari angka adalah angka yang sama dari angka tetapi selalu dengan tanda positif.

Sifat nilai absolut

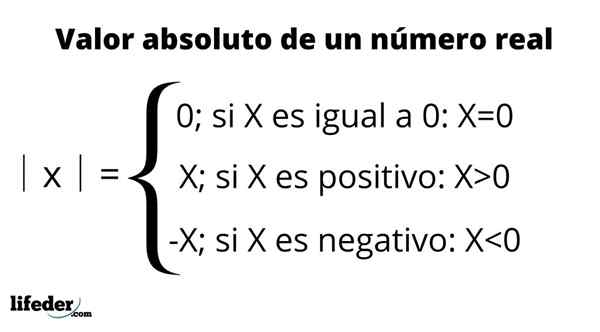Definisi nilai absolut

Properti utama dari nilai absolut:

• 1) Nilai absolut dari suatu angka selalu positif atau 0, oleh karena itu: oleh karena itu:

│x│≥ 0

• 2) Nilai absolut nol juga nol, yaitu │0│ = 0, oleh karena itu dapat ditegaskan bahwa:

│x│ = 0, ya y hanya jika x = 0

• 3) Untuk setiap angka x yang termasuk dalam himpunan bilangan real, nilai absolut x sama dengan nilai absolut - x:

│x│ = │ - x│

• 4) Jika nilai absolut dari angka x adalah A, itu berarti ada dua opsi untuk angka itu: i) x = +a atau ii) x = -a.

Ini dapat melayani Anda: Mary melakukan perjalanan 2/4 dari Cyclepist, Melissa Travels 4/8 dan Anahi Travels 3/6

Misalnya, jika nilai absolut dari suatu angka adalah 5, kedua kemungkinan adalah bahwa angkanya adalah +5 atau -5.

Operasi dengan nilai absolut

Properti berikut sangat berguna untuk melakukan operasi dengan nilai absolut:

• 5) Untuk "x" dan "y" yang merupakan dua bilangan real, ketidaksetaraan berikut selalu terpenuhi, disebut Ketimpangan segitiga dari nilai absolut:

│x│+│y│≥ │x+y│

Misalnya, jadilah:

x = -6

y = 9

Sisi kiri ketidaksetaraan adalah:

│-6│ + │9│ = 6 + 9 = 16

Dan sisi kanan adalah:

│-6+9│ = │3│ = 3

Jelas 16 lebih besar dari atau sama dengan 3, dan ini selalu terjadi ketika angka x dan dan memiliki tanda yang berbeda. Jika mereka memiliki tanda yang sama, maka kesetaraan diperoleh. Lihat contoh lain ini dengan dua nilai berbeda lainnya:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥│-8│

Memang:

8 = 8

• 6) Produk masing -masing nilai absolut dari dua bilangan real "x" dan "y" sama dengan nilai absolut dari produk angka:

│x│ ∙ │y│ = │x ∙ y│

Sekali lagi nilainya:

x = -6

y = 9

Jadi:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Yang sama dengan:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) Kosien nilai absolut dari dua bilangan real "x" dan "y", dengan denominator 0 yang berbeda, adalah nilai absolut dari hasil bagi antara angka -angka ini:

Selama dan ≠ 0.

Contoh:

Contoh nilai absolut

Contoh sederhana

Menghitung nilai absolut dari angka nyata apa pun sangat sederhana, misalnya nilai absolut dari angka -angka berikut adalah:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Perhitungan dengan nilai absolut dari bilangan real

Lakukan operasi berikut yang melibatkan nilai absolut:

a) 2⋅│8│ + 5⋅│ -16│ -⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Dapat melayani Anda: setengah dari 15

Ini adalah operasi gabungan, jadi lebih baik untuk menyelesaikannya dengan langkah -langkah. Nilai absolut pertama adalah:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

Nilai absolut kedua yang muncul dihitung sebagai berikut:

│81 ÷ (-3) │ = │-27│ = 27

Kemudian hasil yang diperoleh dikumpulkan dan perhitungan akhir dilakukan:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19-6 + 27 = 40

Jarak antara dua titik di garis nyata

Nilai absolut muncul dalam banyak aplikasi, seperti menemukan jarak antara dua angka yang termasuk dalam garis nyata. Jika A adalah bilangan real maka terletak di garis nyata pada titik yang absisnya adalah "a", hal yang sama terjadi dengan bilangan real B.

Biarkan "A" dan "B" dua angka di garis nyata, jarak yang memisahkan mereka adalah:

D_AB = │B - a│

Yang juga dapat dihitung dengan:

D_AB = │a - b│

Misalnya, jarak antara a = 5 dan b = 12 adalah:

D = │5−12│ = │12−5│ = 7

Dengan cara ini, nilai absolut dari pengurangan antara dua bilangan real hanyalah jarak yang memisahkannya di garis nyata.

Fungsi nilai absolut

Fungsi nilai absolut adalah aplikasi yang berlaku pada set bilangan real ℛ sampai ℛ⁺, yang sesuai dengan masing -masing bilangan real nilai absolutnya. Itu didefinisikan oleh:

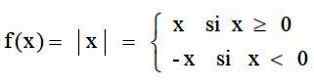
Dan grafiknya memiliki bentuk V khas:

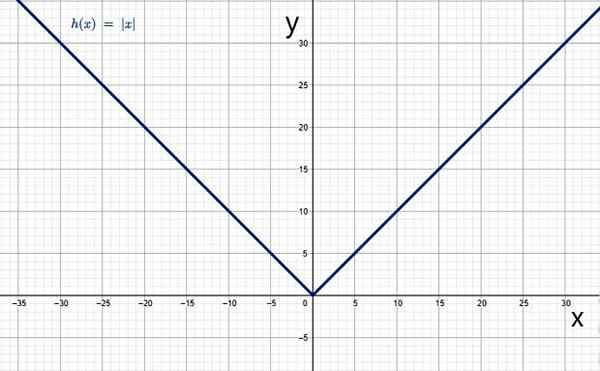Nilai absolut sebagai fungsi. Sumber: f. Zapata melalui Geogebra.

Karakteristik fungsi nilai absolut

-Domain Anda adalah himpunan semua bilangan real.

-Itu terus menerus.

-Bahkan, karena dipenuhi bahwa f (x) = f (-x), oleh karena itu sumbu vertikal adalah sumbu simetri.

-Kisaran fungsi nilai absolut adalah himpunan yang nyata positif termasuk 0, karena fungsi selalu mewakili jarak, dan ini selalu positif atau nol.

Dapat melayani Anda: apa pedomannya? (Geometri)

-Itu adalah fungsi berdasarkan bagian atau bagian.

-Berkurang dalam interval (-∞, 0) dan tumbuh di (0,+∞).

Argumen nilai absolut juga dapat berupa fungsi kuadratik atau lainnya, misalnya, dapat didefinisikan:

• f (x) = │x²-5x+3│
• g (x) = │sen x│

Nilai absolut bertanggung jawab untuk menjadi positif gambar argumen yang memiliki tanda negatif.

Latihan terpecahkan

Latihan 1

Evaluasi ekspresi aljabar berikut dengan nilai absolut:

a) │2x -5│ + │ --x + 1│ pada x = 3

b) │ (x - 5) ÷ (x+4) │ pada x = −1

Solusi untuk

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Solusi b

│ (−1−5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Latihan 2

Apa himpunan nilai yang mewakili ketidaksetaraan berikut?

│x│≤ 3

Larutan

Ketidaksetaraan mewakili semua bilangan real yang nilai absolutnya kurang dari atau sama dengan 3, oleh karena itu merupakan himpunan semua angka antara -3 dan +3, termasuk ini.

Dalam notasi interval tetap:

[-3,3]

Latihan 3

Selesaikan persamaan berikut dengan nilai absolut:

│2x-1│ = 5

Larutan 

Seperti yang ditunjukkan sebelumnya, untuk menyelesaikan persamaan dengan nilai absolut, perlu untuk mempertimbangkan dua opsi. Maksud saya, ya:

│f (x) │ = c

Jadi:

1) f (x) = c

2) f (x) = -c

Oleh karena itu persamaan ini, yang argumennya linier, memiliki dua solusi:

Solusi pertama

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Solusi kedua

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Saat mengevaluasi x₁ = 3 atau x₂ = -2 Dalam persamaan asli kesetaraan harus diperoleh, dengan cara ini diverifikasi bahwa nilai yang diperoleh adalah solusi dari persamaan yang diusulkan. Memang:

│ (2⋅3) -1│ = │6-1│ = 5

Dan ketika mencoba dengan opsi kedua, kesetaraan juga diperoleh:

│2⋅ (-2) -1│ = │-4-1│ = 5

Referensi

1. Baldor, a. 2005. Aljabar. Kelompok tanah air budaya.
2. Larson, r. 2012. Prekalkulasi. Ke -8. Edisi. Pembelajaran Cengage.
3. Hoffman, J. Pemilihan masalah matematika. Volume 2.
4. Stewart, J. 2007. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.