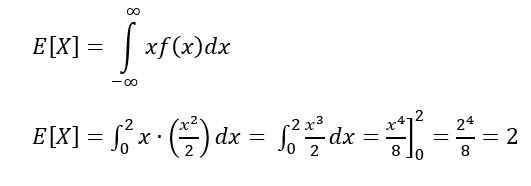Variabel acak kontinu

Kami menjelaskan apa variabel acak kontinu, karakteristiknya, contoh dan latihan yang diselesaikan

Apa variabel acak kontinu?

A Variabel acak kontinu Ini adalah nilai numerik yang diperoleh secara acak, yang hasil dari melakukan percobaan dan dapat mengambil nilai tak terbatas. Ini berarti bahwa, yang diketahui dua nilai berturut -turut dari variabel, selalu mungkin untuk menemukan nilai menengah lainnya di antara mereka.

Dengan memiliki jumlah nilai yang tak terbatas, kumpulan nilai variabel kontinu tidak akuntansi dan hampir selalu termasuk dalam set bilangan real.

Contoh jenis variabel ini adalah status, berat dan suhu tubuh seseorang, tetapi banyak dari mereka dapat ditentukan, beberapa contoh akan ditemukan di bawah. Berbeda dengan variabel acak kontinu, ada variabel acak yang bijaksana, yang merupakan akuntansi, seperti jumlah anak perempuan dalam sebuah keluarga, atau berapa banyak mobil yang dijual oleh agen setelah satu bulan.

Variabel acak diskrit sering mengikuti distribusi probabilitas normal. Sumber: f. Zapata.

Variabel acak kontinu dilambangkan dengan menggunakan huruf modal seperti X, dan nilai -nilai tak terbatas yang diambil variabel adalah hasil yang mungkin dari percobaan acak:

X = x₁, X₂, X₃,… ∞

Setiap nilai memiliki probabilitas kejadian tertentu, dan untuk model yang dengannya probabilitas ini dihitung, disebut distribusi kemungkinan.

Tetapi, karena x mengambil nilai yang tak terbatas, probabilitas untuk nilai spesifik variabel tidak dapat dihitung. Jadi, perlu untuk mendefinisikan fungsi f (x), disebut fungsi distribusi yang terakumulasi, atau hanya fungsi distribusi, yang menurut akumulasi probabilitas dihitung dengan nilai tertentu atau antara dua nilai:

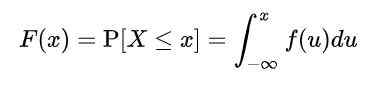
Di mana f (u) menerima nama fungsi kepadatan. Didefinisikan dengan cara ini, F (x) mewakili probabilitas itu X adalah antara -∞ dan X.

Karakteristik variabel acak kontinu

Variabel acak kontinu selesai f (x).

Fungsi kepadatan f (x) Harus memenuhi properti berikut:

• Fungsinya f (x) Itu positif: f (x)> = 0
• Area di bawah kurva y = f (x) Itu selalu sama dengan 1, artinya bahwa probabilitas terjadinya beberapa hasil X Dalam interval (-∞, +∞) adalah 100%.
• Probabilitas bahwa x berada dalam interval [a, b] dihitung dengan integral yang ditentukan berikut:

Dapat melayani Anda: Curtosis: Definisi, Jenis, Rumus, untuk apa, misalnya

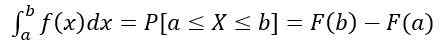
Yang setara dengan area di bawah kurva y = f (x), dipahami antara ke Dan B. Di samping itu:

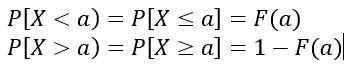
Nilai -nilai f (x) Mereka tidak mewakili probabilitas, jadi P [x = c] = 0. Nilai yang relevan adalah yang sesuai dengan area di bawah kurva y = f (x), yang mewakili probabilitas.

• Dengan menurunkan fungsi distribusi F (x) dengan hormat X, diperoleh f (x).

Grafik f (x) Untuk variabel acak kontinu, ini analog dengan poligon frekuensi yang dibangun untuk variabel statistik diskrit, dengan perbedaan bahwa, untuk variabel acak, lebar interval menjadi sangat kecil tanpa minat.

Harapan

Harapan adalah salah satu ukuran karakteristik dari variabel kontinu. Harapan atau nilai yang diharapkan X Menunjukkan nilai yang diharapkan terjadi lebih sering, dan dihitung melalui integral berikut:

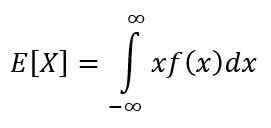
Propertinya adalah:

• E [a∙ x] = a∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+b∙ y] = a∙ e [x] + b∙ e [y]

Dimana jumlahnya ke Dan B Mereka adalah bilangan real.

Contoh

Seperti yang ditunjukkan sebelumnya, ada banyak situasi di mana satu atau lebih variabel acak kontinu dapat didefinisikan. Dalam sains dan bidang lainnya, yang paling umum adalah waktu, panjang, berat, volume dan suhu:

Waktu

Untuk mengoptimalkan proses dan layanan, eksperimen dirancang yang mempelajari waktu yang mereka lakukan untuk dilakukan:

X = waktu yang membawa klien ke jendela bank.

Y = apa yang membutuhkan tempat makanan cepat saji dalam menyajikan pesanan.

Z = waktu di mana reaksi kimia tertentu terjadi.

Statur dan bobot

Dalam banyak penelitian tentang manusia dan hewan, statur dan bobot relevan:

X = tinggi anak perempuan di kursus ke -6. Gelar di setiap sekolah di kota.

Dapat melayani Anda: kongruensi: angka kongruen, kriteria, contoh, latihan

Y = berat bayi saat lahir di rumah sakit umum.

Z = berat sapi di pertanian.

Suhu

Suhu adalah parameter yang relevan dalam berbagai proses kimia, yang biasanya mengambil nilai tak terbatas dalam kisaran tertentu:

X = suhu di mana reaksi kimia tertentu terjadi, mengetahui bahwa ini terjadi antara 80 ºC dan 120 ºC.

Latihan terpecahkan

Latihan 1

Tentukan apa variabel acak kontinu:

1. Jumlah siswa yang menghadiri kopi universitas hari ini.
2. Tekanan darah pasien yang datang ke ruang gawat darurat.
3. Panjang sayap burung, dari spesies yang terancam punah, yang mendiami cadangan.
4. Waktu antara satu orang dan yang lain dirawat di bank.
5. Jumlah produk yang rusak per bulan di pabrik.
6. Kadar kolesterol di ayam pertanian.
7. Jumlah lampu jalan di jalan, total 12.

Larutan

1.- Jumlah siswa yang hadir pada hari itu bisa mati rasa, oleh karena itu, variabel ini tidak kontinu, tetapi bijaksana.

2.- Itu terus menerus. Tekanan darah pasien dapat mengambil nilai apa pun dalam kisaran tertentu.

3.- Variabel kontinu, karena panjang sayap burung mengambil nilai apa pun antara minimum dan maksimum, tergantung pada spesies.

4.- Waktu antara layanan pelanggan adalah variabel dan dapat mengambil nilai apa pun dalam kisaran yang diberikan, misalnya, antara 1 dan 5 menit.

5.- Karena jumlah produk yang rusak adalah akuntansi, ini adalah variabel acak yang bijaksana.

6.- Variabel ini kontinu, karena kadar kolesterol pada ayam mengambil nilai apa pun dalam kisaran yang ditentukan sebelumnya.

Dapat melayani Anda: sudut pelengkap: yang mana dan bagaimana mereka dihitung, contoh, latihan

7.- Bijaksana. Jumlah lampu pencahayaan yang berfungsi adalah jumlah akuntansi.

Latihan 2

Variabel acak kontinu didefinisikan X = "kadar kolesterol " Dalam berbagai ayam pertanian tertentu, yang memiliki fungsi kepadatan berikut f (x):

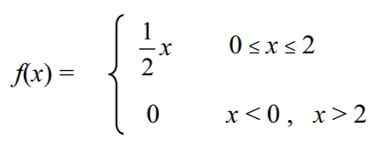
Hitung yang berikut:

1. F (x)
2. P [x ≤2]
3. Harapan MANTAN]

Solusi untuk

Menurut definisi yang diberikan di awal:

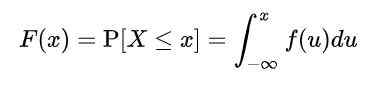
Karena itu, F (x) Itu adalah fungsi di beberapa bagian. Untuk interval X<0, F (x) Itu sama dengan 0, untuk properti yang dinyatakan di awal.

Dalam interval 0≤X≤2, Integral yang tidak terbatas diselesaikan:

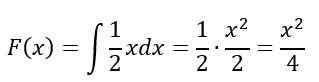
Akhirnya, untuk jeda X> 2, F (x) = 1, Menurut properti, oleh karena itu, F (x) Tetap seperti ini:

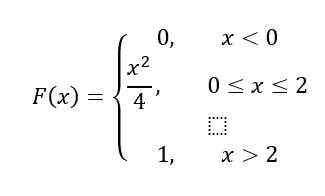
Solusi b

Probabilitas yang dicari adalah F (1.2) dan como x = 1.2 Itu ditemukan di antara 0≤X≤2, itu bagian dari F (x) Untuk mengevaluasi:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Solusi c

Untuk menghitung harapan atau nilai yang diharapkan, ini digunakan: