Pengujian Hipotesis

Apa itu Tes Hipotesis?

Itu Pengujian Hipotesis, Dalam statistik, ini adalah prosedur yang digunakan untuk memeriksa seberapa sukses dugaan tentang a populasi. Dugaan ini disebut hipotesa, bahwa pada prinsipnya mereka dianggap benar, sampai beberapa bukti mengkonfirmasi atau menyangkalnya.

Bukti ini dipasok oleh data sampel, yang berasal dari sebagian besar populasi, yang disebut Sampel. Teori probabilitas memberikan teknik yang diperlukan untuk membandingkan kebenaran hipotesis.

Contoh hipotesis adalah:

-Suhu tubuh manusia rata -rata adalah 36.1 ºC.

-Rata -rata, tas kacang asin yang diproduksi di pabrik makanan ringan dengan berat 50 g.

-80% penduduk kota, melakukan pembelian secara online selama 6 bulan terakhir.

-Nilai tes IQ untuk mahasiswa dari lembaga yang terkenal, memiliki standar deviasi 15.

-Variabel acak tertentu x mengikuti distribusi Poisson.

Empat yang pertama adalah jenis hipotesis parametrik, Karena ini adalah pernyataan tentang beberapa parameter populasi, seperti rata -rata, standar deviasi atau proporsi.

Di sisi lain, hipotesis terakhir menetapkan distribusi variabel acak, dan karena tidak merujuk pada parameter atau properti populasi, dikatakan bahwa itu adalah hipotesis bukan parametrik.

Hipotesis nol dan hipotesis alternatif

Ada dua jenis hipotesis yang dapat digunakan untuk melakukan tes, yang akan berfungsi untuk membandingkannya:

-Hipotesis nol, dilambangkan sebagai h₀, menyatakan bahwa parameter yang diteliti memiliki nilai yang ditetapkan, atau bahwa variabel acak mengikuti distribusi tertentu. Oleh karena itu, dengan mengekspresikan hipotesis nol secara simbolis, simbol kesetaraan selalu digunakan.

-Hipotesis alternatif: disebut h₁, Dia menegaskan bahwa parameter atau distribusi berbeda dari apa yang dipastikan hipotesis nol, karenanya, untuk secara simbolis mengekspresikan hipotesis alternatif, simbol digunakan: atau ≠, tetapi tidak pernah kesetaraan.

Itu dapat melayani Anda: properti aljabar kunci: demonstrasi, contoh

Ketika hipotesis nol diterima, hipotesis alternatif ditolak, sehingga keduanya saling eksklusif.

Tingkat signifikansi

Ini adalah ukuran untuk kesalahan yang dapat dilakukan saat melakukan tes hipotesis. Itu didefinisikan sebagai probabilitas menolak hipotesis nol, adalah bahwa itu benar. Biasanya dilambangkan dengan huruf Yunani α:

α = p (tolak h₀ Bila itu benar)

Nilai yang biasa digunakan untuk α adalah 0.01, 0.05, dan 0.10; menjadi yang kedua yang paling sering digunakan. Setara masing -masing dengan 1%, 5% dan 10% probabilitas membuat kesalahan saat menolak h₀, Namun dalam kasus apa pun, semakin rendah tingkat signifikansi, semakin andal hasil tes.

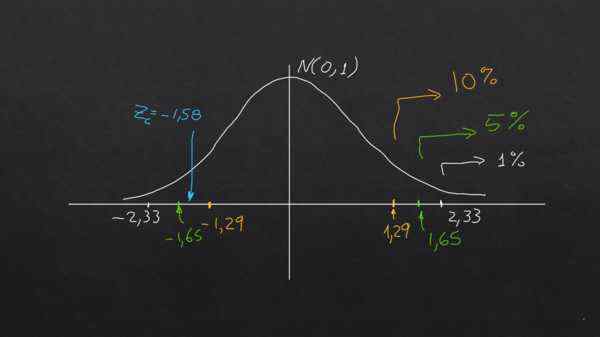
Nilai alfa (α) dapat dipahami sebagai fraksi persentase dari area ekor kanan (atau kiri), dalam distribusi normal yang ditandai (μ = 0 dan σ = 1) dan nilai -nilai ini selalu terjadi pada z = 2,33 untuk α = 0.01; pada z = 1,65 untuk α = 1,65 dan pada z = 1,29 untuk α = 0,1.

Langkah untuk melakukan tes hipotesis

Langkah 1

Tentukan masing -masing hipotesis nol dan alternatif. Hipotesis nol menetapkan bahwa parameter yang diteliti, yang disebut θ, sama dengan nilai referensi, dilambangkan sebagai θ₀:

H₀: θ = θ₀

Misalnya, jika efek obat diselidiki pada karakteristik tertentu dari populasi tikus laboratorium, hipotesis nol merenungkan bahwa obat ini tidak membuat perbedaan dalam karakteristik seperti itu dan bahwa ini memiliki nilai konstan θ₀.

Untuk melambangkan hipotesis nol, tanda kesetaraan selalu digunakan, di sisi lain, hipotesis alternatif memanfaatkan salah satu simbol atau ≠.

Dalam contoh obat, hipotesis alternatif menetapkan bahwa senyawa memang memiliki beberapa efek pada karakteristik yang dimaksud. Oleh karena itu, ini lebih besar, lebih rendah, atau hanya berbeda dari nilai referensi θ₀.

Dapat melayani Anda: notasi faktorial: konsep, contoh dan latihan

Langkah 2

Pilih tingkat signifikansi yang sesuai, yang biasanya ditetapkan pada 5 %, seperti yang ditunjukkan sebelumnya.

Langkah 3

Tentukan populasi dan ekstrak darinya sampel, atau sampel, yang analisisnya akan membandingkan hipotesis dan menentukan penerimaan atau penolakan hipotesis nol.

Langkah 4

Pilih dan hitung nilai statistik percobaan untuk data yang dikumpulkan, dari mana bukti yang diperlukan diperoleh untuk membuat keputusan untuk menerima atau menolak hipotesis nol. Pilihan statistik percobaan tergantung pada parameter yang dipilih: rata -rata, penyimpangan, proporsi atau lainnya.

Statistik uji coba diperoleh dengan mengubah parameter sampel menjadi skor Z, seorang siswa, r Pearson atau statistik chi square, menurut desain eksperimental yang dipilih. Ada formula untuk ini.

Biasanya, jika parameter populasi adalah rata -rata μ, "x bar" adalah rata -rata sampel, standar deviasi σ diketahui dan ukuran sampel adalah n> 30, statistik uji z_C Itu dihitung dengan skor z:

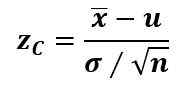
Dan saat n < 30, pero σ es desconocida, se usa la t de Student.

Langkah 5

Menetapkan kriteria untuk penerimaan atau penolakan hipotesis nol, yang dapat dilakukan melalui dua prosedur:

• Melalui nilai p.
• Dengan perbandingan dengan nilai kritis.

Nilai p setara dengan probabilitas mendapatkan hasil yang ditemukan, karena hipotesis nol benar. Jika nilai -nilai ini kecil, hipotesis nol ditolak, jika tidak, itu diterima. Bagaimanapun, nilai p bukan merupakan bukti bahwa hipotesis alternatif itu benar.

Harus diperhitungkan bahwa dalam tes hipotesis dimungkinkan untuk membuat dua jenis kesalahan:

• Jenis I Kesalahan: Tolak h₀ Saat itu benar. Probabilitasnya adalah α dan setara dengan tingkat signifikansi bukti.
• Tipe II Kesalahan: Terima h₀ Saat itu benar -benar salah. Probabilitasnya dilambangkan sebagai β.

Itu dapat melayani Anda: apa hubungan antara area belah ketupat dan persegi panjang?

Langkah 6

Membuat keputusan untuk menerima atau menolak hipotesis nol. Jika nilai p digunakan, saat p < α, se rechaza H₀ Dan h diterima₁, Dan sebaliknya, H diterima₀. Himpunan nilai p < α se conoce como wilayah kritis. Jika statistik dalam interval ini, H ditolak₀.

Demikian pula, nilai kritis dipilih, sesuai dengan parameter populasi yang dipilih. Jika ini rata -rata, lanjutkan sebagai berikut:

• Uji Ekor: θ < θ₀ atau θ> θ₀
• Tes Two Tails: | θ | < θ₀

Contoh terpecahkan

Mesin memproduksi sekrup yang nilai nomangkalnya harus panjang 800 milimeter, dengan standar deviasi 5%.

Sampel acak diambil, yaitu, pada hari yang berbeda dari minggu produksi, yang total sekitar 40 sekrup. Ketika panjang rata -rata sampel dihitung, nilai 790 milimeter diperoleh.

Tentukan apakah panjang rata -rata dalam toleransi dengan tingkat signifikansi masing -masing 1%, 5% dan 10%.

Larutan

Yang pertama adalah menghitung statistik uji rata -rata, yang dalam hal ini adalah penyimpangan rata -rata yang terbagi antara kesalahan populasi standar:

Zc = (790 - 800) / (40 / √40) = -1,58

Di mana telah diperhitungkan bahwa 5% standar deviasi sesuai dengan 40 dari 800.

Hipotesis nol adalah bahwa sampel rata -rata berada dalam toleransi yang diizinkan untuk tingkat signifikansi yang diperlukan, dengan ketentuan bahwa | zc | kurang dari nilai yang ditiru | zt |, jika tidak, hipotesis nol ditolak.

Untuk signifikansi 1% dan 5%, hipotesis nol dipenuhi, karena | zc | < 2,33 y |Zc| < 1,65 respectivamente.

Namun, untuk signifikansi 10% itu terjadi bahwa | zc | > 1.29. Yaitu, pada tingkat signifikansi ini hipotesis nol tidak terpenuhi.

Grafik berikut mengklarifikasi kesimpulan:

Grafik menunjukkan tergantung pada tingkat signifikansi yang diperlukan hipotesis yang sama dapat diterima atau ditolak dengan data yang sama. Sumber: f. Zapata.