Matematika

Variasi proporsional

Variasi proporsional

Apa itu variasi proporsional?

Variasi proporsional antara dua variabel "x" dan "y" terjadi ketika, dengan mengalikan salah satunya dengan satu konstanta, yang lain juga dikalikan atau dibagi dengan konstanta yang sama. Banyak situasi dunia nyata dapat dijelaskan dengan baik dengan mereka.

Proporsionalitas antara variabel bisa langsung atau terbalik. Dalam proporsionalitas langsung, hubungannya adalah tipe:

y = k ∙ x

Atau setara:

K = y/x

Di mana k adalah konstanta yang disebut Proporsionalitas konstan salah satu rasio proporsionalitas. Perhatikan bahwa jika "x" meningkat, "y" melakukannya dalam proporsi yang sama, dan jika "x" berkurang, itu juga akan "y". Ketika hubungan antara variabel adalah grafik, garis lurus diperoleh yang melewati asal sistem koordinat (lihat latihan diselesaikan nanti).

Variasi langsung juga dapat terjadi antara satu variabel dan satu kekuatan yang lain, misalnya, "y" dapat secara langsung sebanding dengan x2, X3 dan sebagainya.

Di sisi lain, dalam proporsionalitas terbalik, variabel dihubungkan melalui ekspresi:

x ∙ y = k

Ekspresi ini berarti bahwa produk variabel adalah konstan. Saat memberi grafik hubungan antara variabel adalah hiperbola. Juga, jika produk dari suatu variabel dengan satu kekuatan yang lain konstan, itu juga merupakan kasus proporsionalitas terbalik, misalnya:

X2∙ y = k; X3∙ y = k ..

Contoh

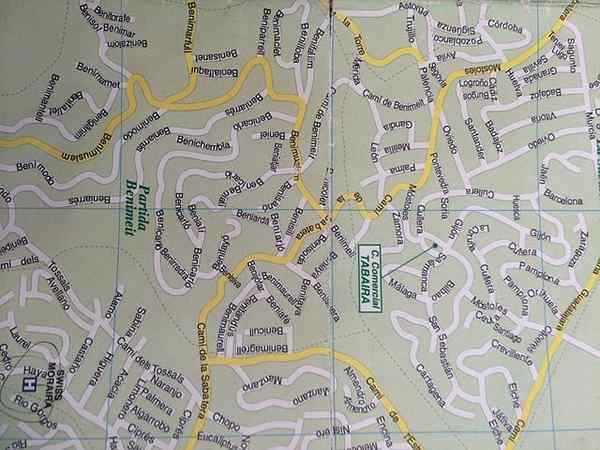Aplikasi variasi proporsional adalah tata letak peta

Banyak hukum fisika dan kimia diekspresikan secara matematis sebagai proporsi. Misalnya, gaya yang mengerahkan pegas dan perpanjangan yang sama, hubungan antara tekanan dan volume dalam gas pada suhu konstan, periode pendulum sederhana dan akar kuadrat dari panjangnya dan banyak lagi. Mengetahui model yang mengatur fenomena, Anda dapat mengetahui perilaku Anda untuk nilai variabel apa pun.

Dapat melayani Anda: Teorema Keberadaan dan Keunikan: Demonstrasi, Contoh dan Latihan

Dan tidak hanya itu, mereka juga berlaku dalam situasi yang tak terhitung jumlahnya seperti ini:

  • Lewati pola pakaian dengan ukuran yang lebih kecil ke ukuran yang lebih besar (atau sebaliknya).
  • Dalam faktor konversi, untuk berpindah dari satu unit ke unit lainnya, seperti kilometer ke mil, galon ke liter dan banyak lagi.
  • Hitung bahan resep untuk 6 orang yang mengetahui persyaratan untuk 4 orang.
  • Tentukan jumlah pajak tertentu sesuai dengan pendapatan yang diperoleh.
  • Dalam perhitungan bunga sederhana.
  • Saat menggambar pesawat pada skala.
  • Ketika Anda harus menghitung harga sejumlah produk yang mengetahui harga unit.
  • Dalam kesamaan segitiga.

Selanjutnya, secara rinci, ada dua situasi menarik di mana variasi proporsional berlaku:

Contoh 1

Pada skala sebuah kota, Hermitage Avenue mengukur 3.2 cm, menjadi panjang sebenarnya 400 m. Di sisi lain, jalan La Fuente, yang benar -benar berukuran 180 m harus menggambar dengan stroke yang lebih pendek secara proporsional. Berapa ukuran stroke?

Pernyataan tersebut menawarkan informasi lengkap dari Jalan Ermita: Biarkan panjang sebenarnya dari jalan dan ℓ panjangnya di pesawat, karena variasinya adalah proporsionalitas langsung, ia harus:

L = k ∙ ℓ

Dari data di Hermitage Avenue Anda dapat mengetahui nilai konstanta proporsionalitas K, tetapi sebelum perlu untuk meninggalkan semua panjang dalam unit yang sama:

3.2 cm = 0.032 m

Jadi:

400 m = k ∙ 0.032 m

Oleh karena itu konstanta proporsionalitas adalah:

Dapat melayani Anda: apa elemen perumpamaan? (Bagian)

K = 400 /0.032 = 12500

Sekarang diketahui bahwa:

L = 12500 ∙ ℓ

Hasil ini ditafsirkan sebagai berikut: Panjang jalanan di peta ini 12500 kali lebih kecil dari panjang sebenarnya. Oleh karena itu garis jalan La Fuente mengukur:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Contoh 2

Seorang analis memiliki tabel nilai berikut untuk variabel "x" dan "y" yang diperoleh secara eksperimental dan ingin tahu apakah data ini sesuai dengan model variasi proporsional langsung atau salah satu dari variasi proporsional terbalik.

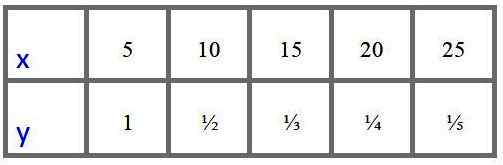
Apa yang harus Anda lakukan untuk diketahui?

Pertama -tama diamati bahwa ketika "x" meningkat, "y" berkurang, sehingga mencurigai proporsionalitas terbalik, dalam hal apa pun, untuk memastikan, analis memiliki opsi untuk menilai apakah hasil bagi dan/x konstan (proporsional variasi langsung) atau jika produk x.dan konstan (variasi proporsional terbalik).

Menguji dengan opsi pertama:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Disimpulkan bahwa itu bukan variasi proporsional langsung, karena hasil bagi dan/x memberikan nilai yang berbeda untuk setiap pasangan data.

Kita perlu memeriksa apakah produk x ∙ konstan:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

Dan sebagai produk x ∙ y = 5 disimpulkan bahwa variasinya adalah proporsionalitas terbalik.

Informasi ini berfungsi untuk mengetahui nilai -nilai yang tidak ada dalam tabel, misalnya, apa nilai "y" ketika x = 30?

Dari x ∙ y = 5, "y" dibersihkan dan diganti x = 30:

y = 5/x

y = 5/30 = 1/6

Olahraga diselesaikan

Jika biaya meter kain 6.$ 75, dan mengetahui bahwa harganya berbanding lurus dengan jumlah meter untuk dibeli, temukan:

Itu dapat melayani Anda: antiderivatif: rumus dan persamaan, contoh, latihan

a) Ekspresi aljabar yang menghubungkan variabel "harga dengan $" dan "jumlah meter kain".

b) Siapkan tabel nilai dengan harga untuk 3, 6, 9, 12, 15 dan 18 meter kain.

c) grafik nilai yang diperoleh.

Menjawab

Biarkan "y" variabel "harga dengan $" dan "x" variabel "jumlah meter kain". Seperti proporsional langsung, Anda harus:

y = k ∙ x

Untuk x = 1 meter, y = 6.$ 75, oleh karena itu k = 6.75 $/meter. Ini adalah harga satuan kain, harga kain "x" lainnya diperoleh dengan mengalikan dengan nilai ini, maka, ekspresi aljabar yang dicari adalah:

y = 6.75 ∙ x

Jawaban b

Tabel nilai dengan harga pada $ untuk 3, 6, 9, 12, 15 dan 18 meter adalah:

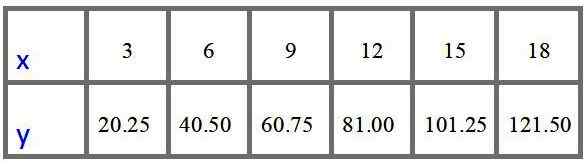
Jawaban c

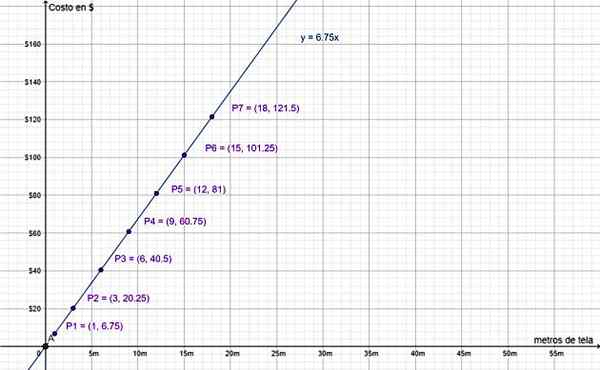
Akhirnya, grafik nilai dalam tabel sebelumnya menguatkan bahwa itu adalah variasi proporsional langsung:

Biaya $ dan jumlah meter kain secara langsung proporsional. Sumber: f. Zapata.

Perhatikan bahwa nilai (0,0) disertakan, karena baris y = 6.75 ∙ x melewati asal sistem koordinat, seperti yang dijelaskan sebelumnya. Masuk akal, karena tidak melakukan pembelian setara dengan membeli 0 m kain, yang nilainya 0 $.

Referensi

  1. Larson, r. 2012. Pra-patung. Ke -8. Edisi. Pembelajaran Cengage.
  2. Sekretariat Pendidikan Publik Meksiko. Variasi proporsional. Diperoleh dari: PPS.K12.Atau.kita.
  3. Stewart, J. 2007. Pra-kalkulasi: Matematika untuk perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
  4. Unam. Panduan belajar: Matematika I. Pulih dari: Dirre.Unam.MX.
  5. Zill, d. 2008. Pra-kalkulasi dengan kemajuan perhitungan. 4. Edisi. Bukit McGraw.