Karakteristik dan sifat vektor, elemen, jenis, contoh

Itu Vektor Mereka adalah entitas matematika yang memiliki besar -besaran -positif -, biasanya disertai dengan satuan ukuran, di samping arah dan makna. Karakteristik seperti itu sangat tepat untuk menggambarkan jumlah fisik seperti kecepatan, kekuatan, akselerasi dan banyak lagi.

Dengan vektor dimungkinkan untuk melakukan operasi seperti jumlah, pengurangan dan produk. Divisi ini tidak didefinisikan untuk vektor dan untuk produk, ada tiga kelas yang akan kami jelaskan nanti: produk skalar atau titik, vektor atau produk silang dan produk skalar untuk vektor.

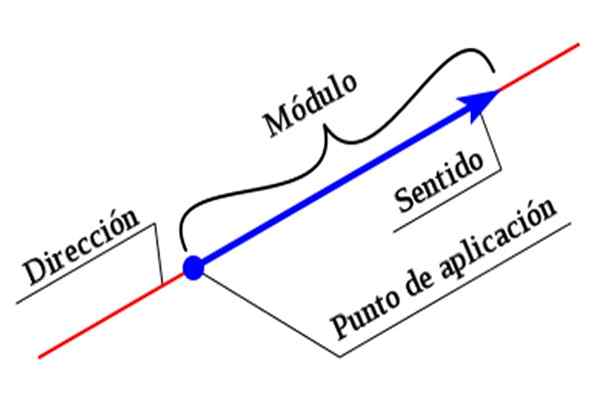Gambar 1. Elemen vektor. Sumber: Wikimedia Commons.

Untuk sepenuhnya menggambarkan vektor, perlu untuk menunjukkan semua karakteristiknya. Besarnya atau modul adalah nilai numerik disertai dengan unit, sedangkan arah dan makna ditetapkan dengan bantuan sistem koordinat.

Mari kita lihat contoh: Misalkan pesawat terbang dari satu kota ke kota lain dengan kecepatan 850 km/jam ke arah. Di sini kami memiliki vektor yang sepenuhnya ditentukan, karena besarnya tersedia: 850 km/jam, sedangkan arah dan makna adalah NE.

Vektor biasanya diwakili secara grafis oleh segmen garis berorientasi, yang panjangnya sebanding dengan besarnya.

Sementara untuk menentukan arah dan artinya, garis referensi diperlukan yang biasanya merupakan sumbu horizontal, meskipun utara juga dapat dianggap sebagai referensi, seperti kasus kecepatan pesawat:

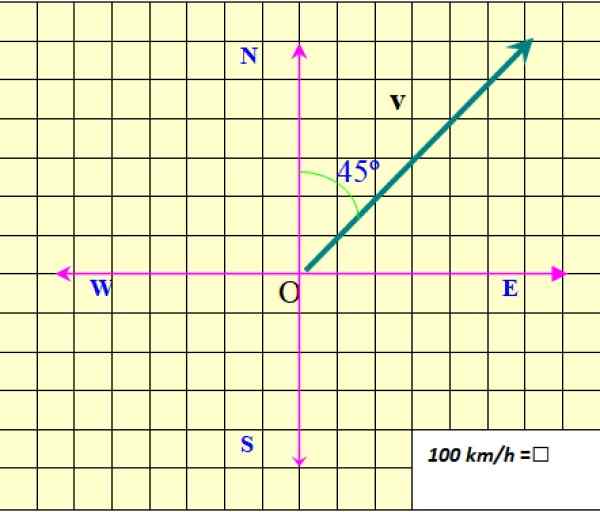Gambar 2. Vektor kecepatan. Sumber: f. Zapata.

Gambar tersebut menunjukkan vektor kecepatan pesawat, yang dilambangkan v di dalam berani, untuk membedakannya dari kuantitas skalar, yang hanya membutuhkan nilai numerik dan beberapa unit untuk ditentukan.

[TOC]

Elemen vektor

Seperti yang telah kami katakan, elemen vektor adalah:

-Magnitudo atau modul, kadang -kadang juga disebut nilai absolut atau standar vektor.

-Alamat

-Nalar

Dalam contoh Gambar 2, modul v Itu 850 km/jam. Modul dilambangkan sebagai V tanpa tebal, atau sebagai |v|, Di mana bilah mewakili nilai absolut.

Alamat v ditentukan sehubungan dengan utara. Dalam hal ini 45º di utara timur (45º NE). Akhirnya ujung panah menginformasikan tentang arah v.

Dalam contoh ini, asal vektor telah ditarik dengan bertepatan dengan sistem asal atau koordinat, ini dikenal sebagai Vektor tertaut. Di sisi lain, jika asal vektor tidak cocok dengan sistem referensi, dikatakan bahwa itu adalah a vektor gratis.

Perlu dicatat bahwa untuk sepenuhnya menentukan vektor, ketiga elemen ini harus diindikasikan, jika tidak deskripsi vektor tidak akan lengkap.

Komponen persegi panjang dari vektor

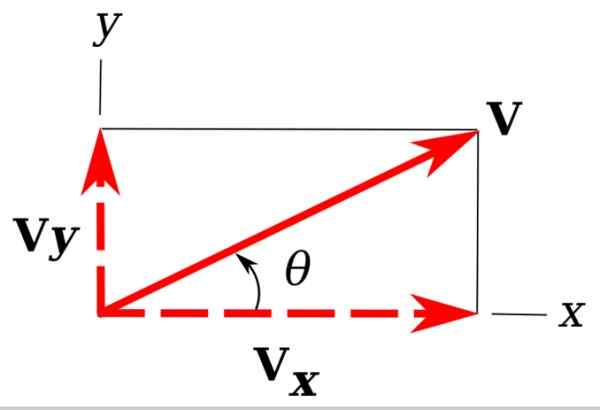Gambar 3. Komponen persegi panjang vektor di pesawat. Sumber: Wikimedia Commons. Unther [cc by-sa 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)]

Dalam gambar kami memiliki kembali contoh vektor kami v, itu ada di pesawat Xy.

Sangat mudah untuk memperhatikan bahwa proyeksi V pada sumbu koordinat x dan y menentukan segitiga siku -siku. Proyeksi ini v_Dan Dan v_X dan disebut komponen persegi panjang v.

Cara untuk menunjukkan v Melalui komponen persegi panjangnya seperti ini: v = X, v_Dan>. Kurung persegi ini digunakan sebagai pengganti tanda kurung untuk menekankan fakta bahwa itu adalah vektor dan bukan titik, karena dalam hal ini tanda kurung akan digunakan.

Dapat melayani Anda: James Chadwick: Biografi, Model Atom, Eksperimen

Jika vektor berada dalam ruang tiga -dimensi, satu komponen lagi diperlukan, sehingga:

v = X, v_Dan, v_z>

Mengetahui komponen persegi panjang, besarnya vektor dihitung, setara dengan menemukan hypotenuse dari segitiga kanan yang kakinya v_X Dan v_Dan,. Melalui teorema Pythagoras, itu mengikuti itu:

|v|² = (v_X)² +  (v_Dan)²

Bentuk vektor kutub

Saat besarnya vektor diketahui |v| Dan sudut θ bahwa bentuk ini dengan sumbu referensi, biasanya sumbu horizontal, vektor juga ditentukan sama. Kemudian dikatakan bahwa vektor dinyatakan dalam bentuk kutub.

Komponen persegi panjang dalam hal ini mudah dihitung:

v_X = |v|.cos θ

v_Dan = |v|.dosa θ

Menurut yang di atas, komponen persegi panjang dari vektor kecepatan v pesawat akan menjadi:

v_X = 850 . cos 45º km/jam = 601.04 km/jam

v_Dan = 850 . Sen 45º km/jam = 601.04 km/jam

Teman-teman

Ada berbagai jenis vektor. Ada vektor urat, posisi, perpindahan, gaya, medan listrik, jumlah gerakan dan banyak lagi. Seperti yang telah kami katakan, dalam fisika ada banyak besaran vektor.

Adapun vektor yang memiliki karakteristik tertentu, kita dapat menyebutkan jenis vektor berikut:

-Batal: Ini adalah vektor yang besarnya 0 dan yang dilambangkan 0. Ingatlah bahwa huruf tebal melambangkan tiga karakteristik dasar vektor, sedangkan huruf normal hanya mewakili modul.

Misalnya tentang tubuh dalam keseimbangan statis, jumlah kekuatan harus menjadi vektor nol.

-Gratis dan ditautkan: Vektor gratis adalah mereka yang titik asal dan kedatangannya adalah sepasang titik pesawat atau ruang, tidak seperti vektor terkait, yang aslinya bertepatan dengan sistem referensi yang digunakan untuk menggambarkannya.

Pasangan atau momen yang diproduksi oleh beberapa kekuatan adalah contoh yang baik dari vektor gratis, karena torsi tidak berlaku untuk beberapa titik tertentu.

-Peralatan: Mereka adalah dua vektor gratis yang memiliki karakteristik yang identik. Oleh karena itu mereka memiliki besarnya, arah, dan makna yang sama.

-Coplanares atau coplanarios: vektor milik pesawat yang sama.

-Lawan: vektor dengan besarnya dan arah yang sama, tetapi indera yang berlawanan. Vektor menentang vektor v Itu adalah vektor -v Dan jumlah keduanya adalah vektor nol: v + (-v) = 0.

-Bersamaan: vektor yang garis aksi semuanya melewati titik yang sama.

-Menggeser: Apakah vektor -vektor yang titik aplikasinya dapat meluncur di sepanjang garis tertentu.

-Colineal: vektor yang terletak di jalur yang sama.

-Unitari: Vektor -vektor yang modulnya adalah 1.

Vektor unit ortogonal

Ada jenis vektor yang sangat berguna dalam fisika yang disebut vektor unit ortogonal. Vektor unit ortogonal memiliki modul yang sama dengan 1 dan unit dapat ada, misalnya yang memiliki kecepatan, posisi, kekuatan atau lainnya.

Ada satu set vektor khusus yang membantu dengan mudah mewakili vektor lain dan melakukan operasi dengan mereka: mereka adalah vektor unit ortogonal yo, J Dan k, Unitari dan tegak lurus satu sama lain.

Dalam dua dimensi, vektor -vektor ini diarahkan pada pengertian positif dari kedua sumbu X pada poros Dan. Dan dalam tiga dimensi vektor unit ditambahkan ke arah sumbu z positif. Mereka diwakili sebagai berikut:

Dapat melayani Anda: apa struktur penelitian dokumenter?

yo =

J =

k =

Vektor dapat diwakili oleh vektor unit yo, J Dan k sebagai berikut:

v = v_X yo + v_Dan J + v_z k

Misalnya vektor kecepatan v Dari contoh sebelumnya, Anda dapat menulis sebagai:

v = 601.04 yo + 601.04 J km/h

Komponen di k Itu tidak perlu, karena vektor ini ada di pesawat.

Jumlah vektor

Jumlah vektor muncul sangat sering dalam berbagai situasi, misalnya ketika Anda ingin menemukan kekuatan yang dihasilkan pada objek yang dipengaruhi oleh berbagai kekuatan. Untuk memulai anggaplah Anda memiliki dua vektor gratis atau Dan v Di pesawat, seperti yang berikut ini menunjukkan kiri:

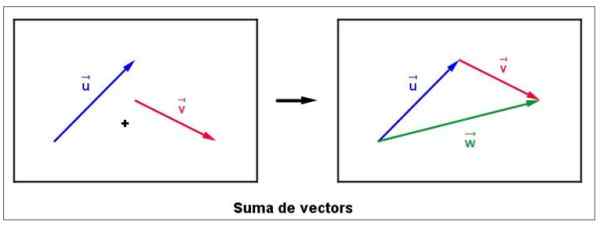Gambar 4. Jumlah grafis dari dua vektor. Sumber: Wikimedia Commons. LLUC CABANACH [CC BY-SA 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)].

Dia segera pindah ke vektor v, tanpa memodifikasi besarnya, arah, atau maknanya, sehingga berasal dari ujungnya atau.

Jumlah vektor disebut W dan ditarik mulai dari Anda berakhir v, Menurut sosok yang tepat. Penting untuk dicatat bahwa besarnya vektor W Itu belum tentu jumlah besarnya v Dan atau.

Jika dipantulkan dengan cermat dalam hal ini, satu -satunya kesempatan ketika besarnya vektor yang dihasilkan adalah jumlah besarnya addends, itu adalah ketika kedua pecandu berada dalam arah yang sama dan memiliki arti yang sama.

Dan apa yang terjadi jika vektor tidak gratis? Juga sangat mudah untuk menambahkannya. Cara yang harus dilakukan adalah menambahkan komponen komponen, atau metode analitik.

Sebagai contoh, mari kita pertimbangkan vektor dari gambar berikut, hal pertama adalah mengekspresikannya dari salah satu bentuk Cartesian yang sebelumnya dijelaskan:

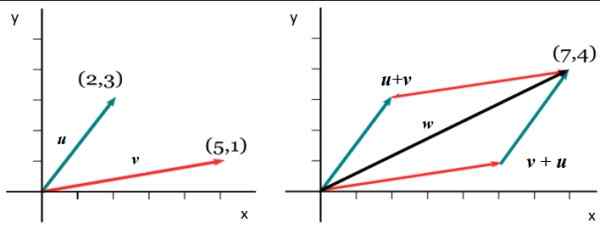Gambar 5. Jumlah dari dua vektor terkait. Sumber: Wikimedia Commons.

v =

atau =

Untuk mendapatkan komponen di X dari vektor menambahkan W, Komponen masing -masing ditambahkan X dari v Dan atau: W_X = 5+2 = 7. Dan untuk mendapatkan W_Dan Prosedur analog diikuti: w_Dan = 1+3. Karena itu:

atau =

Sifat jumlah vektor

-Jumlah dua atau lebih vektor menghasilkan vektor lain.

-Itu adalah komutatif, urutan penambahan tidak mengubah jumlah, sehingga:

atau + v = v + atau

-Elemen netral dari jumlah vektor adalah vektor nol: v + 0 = v

-Pengurangan dua vektor didefinisikan sebagai jumlah yang berlawanan: v - u = v + (-atau)

Contoh vektor

Seperti yang telah kami katakan, ada banyak jumlah vektor dalam fisika. Di antara yang paling terkenal adalah:

-Posisi

-Pemindahan

-Kecepatan rata -rata dan kecepatan instan

-Percepatan

-Memaksa

-Jumlah gerakan

-Torsi atau momen kekuatan

-Impuls

-Medan listrik

-Medan gaya

-Momen magnetik

Di sisi lain mereka bukan vektor tetapi memanjat:

-Waktu

-Massa

-Suhu

-Volume

-Kepadatan

-Pekerjaan mekanis

-Energi

-Panas

-Kekuatan

-Tegangan

-Arus listrik

Operasi lain antar vektor

Selain jumlah dan pengurangan vektor, ada tiga operasi lain antara vektor yang sangat penting, karena mereka memunculkan besaran fisik baru yang sangat penting:

-Produk skalar untuk vektor.

-Produk skalar atau produk titik antar vektor

-Dan produk salib atau vektor antara dua vektor.

Produk skalar untuk vektor

Pertimbangkan hukum kedua Newton, yang menyatakan kekuatan itu F dan percepatan ke Mereka proporsional. Konstanta proporsionalitas adalah massa M Objek, oleh karena itu:

F = m.ke

Adonan adalah skalar; Untuk bagiannya, kekuatan dan akselerasi adalah vektor. Karena gaya diperoleh dengan mengalikan massa dengan akselerasi, itu adalah hasil dari produk skalar dengan vektor.

Dapat melayani Anda: contoh kerangka teori

Jenis produk ini selalu menghasilkan vektor. Di sini contoh lain: jumlah gerakan. Menjadi P Jumlah Gerakan Vektor, v Vektor kecepatan dan seperti biasa, M adalah massa:

P = m.v

Produk skalar atau produk titik antar vektor

Kami telah menempatkan pekerjaan mekanis dalam daftar besaran yang bukan vektor. Namun, pekerjaan dalam fisika adalah hasil dari operasi antara vektor yang disebut produk skalar, produk internal atau produk titik.

Jadilah vektor v Dan atau, Titik atau produk pendakian didefinisikan di antara mereka:

v∙atau = |v| ∙ |atau |.cos θ

Menjadi θ sudut di antara mereka. Dari persamaan yang ditunjukkan segera disimpulkan bahwa hasil produk titik adalah skalar dan juga bahwa jika kedua vektor tegak lurus, produk skalar mereka adalah 0.

Kembali ke pekerjaan mekanis W, Ini adalah produk skalar antara vektor kekuatan F dan perpindahan vektor ℓ.

W = F∙ℓ                  

Ketika vektor tersedia dalam hal komponennya, produk titik juga sangat sederhana untuk dihitung. Ya v = X, v_Dan, v_z > Dan atau = X, atau_Dan, atau_z >, Produk titik di antara keduanya adalah:

v∙atau = v_X atau_X + v_Dan atau_Dan + v_z atau_z

Produk titik antara vektor adalah komutatif, oleh karena itu:

v∙atau = atau∙v

Produk lintas produk atau vektor antar vektor

Ya v dan Anda adalah dua contoh vektor kami, produk vektor didefinisikan sebagai:

v X atau = W

Segera mengikuti bahwa produk silang menghasilkan vektor, yang modulnya didefinisikan sebagai:

|v X u | = | V | . | u |. dosa θ

Di mana θ Itu adalah sudut antara vektor.

Produk silang tidak komutatif, karenanya v X u ≠ u X v. nyatanya v X U = - (u X V).

Jika dua contoh vektor dinyatakan dalam hal vektor unit, perhitungan produk vektor difasilitasi:

v = v_X yo + v_Dan J + v_z k

atau = u_X yo + atau_Dan J + atau_z k

Produk silang antar vektor unit

Produk silang antara vektor unit identik adalah nol, karena sudut di antara mereka adalah 0º. Tetapi di antara vektor unit yang berbeda, sudut di antara mereka adalah 90º dan sin 90º = 1.

Skema berikut membantu menemukan produk ini. Ke arah panah itu masuk akal dan dalam arah yang berlawanan:

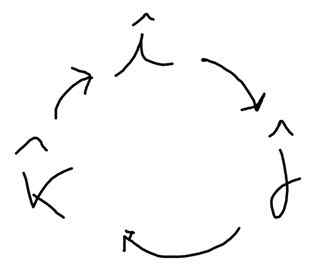
yo X J = K, J X k = Yo; k X yo = J; J X i = -k; k X J = -Yo; yo X k = -J

Menerapkan properti distributif, yang tetap berlaku untuk produk di antara vektor ditambah properti vektor unit, Anda memiliki:

v X atau = (v_X yo + v_Dan J + v_z k) X (u_X yo + atau_Dan J + atau_z k) =  

= (v_Danatau_z - v_zatau_Dan )yo + (v_zatau_X - v_Xatau_z )J + (v_Xatau_Dan - v_Danatau_X )k

Latihan terpecahkan

- Latihan 1

Diberikan vektor:

v = -5 yo + 4J + 1 k

atau = 2 yo -3 J + 7k

Apa yang seharusnya menjadi vektor W sehingga jumlahnya v + atau + W Hasil 6 yo +8 J -10k?

Larutan

-5 yo + 4J + 1 k

2 yo -3 J + 7k

 W_X yo + W_Dan J + W_z k  +

--

6yo + 8 J -10 k

Karena itu harus dipenuhi bahwa:

-5 +2 + w_X = 6 → w_X = 9

4-3 + w_Dan = 8 → w_Dan = 7

1 + 7 + w_z = -10 → w_z = -18

Jawabannya adalah: W = 9 yo +7 J - 18k

- Latihan 2

Apa sudut antara vektor v Dan atau Latihan 1?

Larutan

Kami akan menggunakan produk skalar. Kita punya:

cos θ = v∙atau / |v| ∙ |atau|

v∙atau= -10 -12+7 = -15

|v| = √ (-5)² +4² +1²= √42 = 6.48

|atau| = √2² +(-3)² +7²= √62 = 7.87

Mengganti nilai -nilai ini:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → θ = 107.1st

Referensi

1. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
2. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
3. Rex, a. 2011. Dasar -dasar fisika. Pearson.
4. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.
5. Serway, r., Jewett, J. 2008. Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage.