Persamaan Direktur Vektor dari Garis, Latihan Terpecahkan
- 1915
- 558
- Herbert Fritsch
Itu dipahami oleh Direktur Vektor orang yang mendefinisikan arah garis, baik di pesawat atau di luar angkasa. Oleh karena itu, vektor yang sejajar dengan garis dapat dianggap sebagai direktur yang sama.
Ini dimungkinkan berkat aksioma geometri Euclidean yang mengatakan bahwa dua poin menentukan garis. Kemudian segmen berorientasi yang membentuk kedua poin ini juga mendefinisikan direktur vektor dari baris itu.
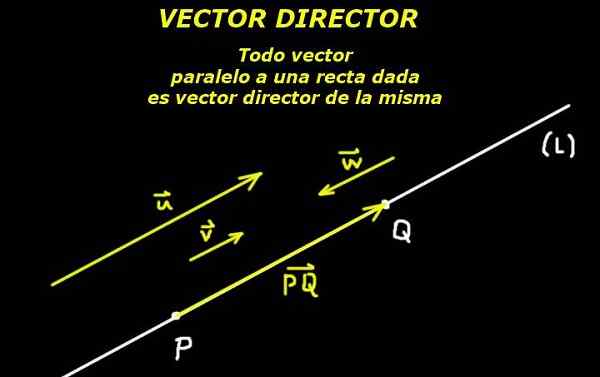Gambar 1. Direktur Vektor Line. (Elaborasi sendiri) Diberi poin P milik garis (L) dan memberikan vektor direktur atau Dari garis itu, garis sepenuhnya ditentukan.
[TOC]
Persamaan Line dan Direktur Direktur
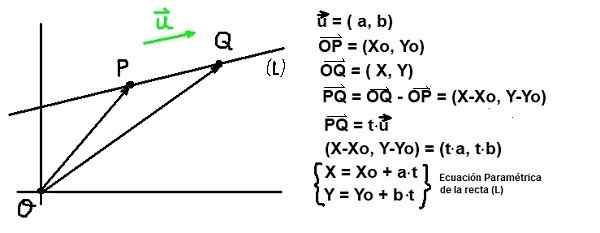
Gambar 2. Persamaan Line dan Direktur Direktur. (Elaborasi sendiri) Diberi poin P koordinat T: (xo, saya) dan vektor atau Direktur A Line (L), Semua titik Q koordinat T: (x, y) harus memenuhi vektor itu PQ sejajar dengan u. Kondisi terakhir ini dijamin jika PQ Itu sebanding dengan atau:
PQ = t⋅atau
Di ekspresi sebelumnya T Itu adalah parameter yang termasuk dalam bilangan real.
Jika komponen cartesian dari PQ dan dari atau Persamaan sebelumnya ditulis sebagai berikut:
(X-xo, y-yo) = t⋅ (a, b)
Jika komponen kesetaraan vektor sama dengan pasangan persamaan berikut:
X - xo = a⋅t Dan Dan - me = b⋅t
Persamaan parametrik dari garis
Koordinat X Dan DAN dari suatu titik milik garis (L) yang melewati titik koordinat (Xo, saya) Dan itu paralel dengan Direktur Vektor atau= (a, b) Mereka ditentukan dengan menetapkan nilai nyata ke parameter variabel T:
X = xo + a⋅t; Y = me + b⋅t
Contoh 1
Untuk mengilustrasikan arti persamaan parametrik dari garis, kami mengambil sebagai direktur vektor
Dapat melayani Anda: optik bergelombangatau = (a, b) = (2, -1)
dan sebagai titik garis yang diketahui
P = (xo, me) = (1, 5).
Persamaan parametrik garis adalah:
X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞
Untuk menggambarkan arti persamaan ini Gambar 3 menunjukkan, di mana parameter t mengubah nilai dan titik Q koordinat (X, y) Mengambil posisi berbeda di telepon.
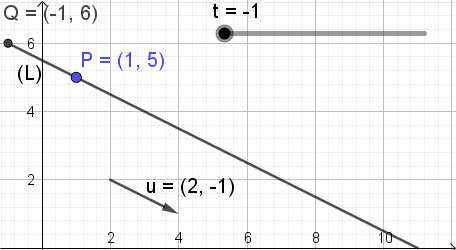Gambar 3. Pq = t u. (Elaborasi sendiri) Garis dalam bentuk vektor
Diberi titik P dari garis dan direktur direkturnya atau persamaan garis dapat ditulis dalam bentuk vektor:
Oq = Op + λ⋅atau
Dalam persamaan sebelumnya itu adalah titik mana pun tetapi milik garis dan λ Bilangan real.
Persamaan vektor garis berlaku untuk sejumlah dimensi, bahkan hyper-eret dapat didefinisikan.
Dalam kasus tiga dimensi untuk vektor direktur atau= (a, b, c) dan satu poin P = (xo, saya, zo), Koordinat titik generik Q = (x, y, z) Milik garis adalah:
(X dan z) = (Xo, i, zo) + λ⋅ (a, b, c)
Contoh 2
Pertimbangkan lagi garis yang memiliki Direktur Direktur
atau = (a, b) = (2, -1)
dan sebagai titik garis yang diketahui
P = (xo, me) = (1, 5).
Persamaan vektor dari garis ini adalah:
(X, y) = (1, 5) + λ⋅ (2, -1)
Bentuk kontinu dari garis dan vektor direktur
Mulai dari bentuk parametrik, membersihkan dan mencocokkan parameter λ yang Anda miliki:
(X-xo)/a = (y-yo)/b = (z-zo)/c
Ini adalah bentuk simetris dari persamaan garis. aku merasakannya ke, B Dan C Mereka adalah komponen dari vektor direktur.
Contoh 3
Pertimbangkan garis yang memiliki Direktur Direktur
atau = (a, b) = (2, -1)
dan sebagai titik garis yang diketahui
Dapat melayani Anda: apa listriknya? (Dengan percobaan)P = (xo, me) = (1, 5). Temukan bentuk simetrisnya.
Bentuk simetris atau kontinu dari garis adalah:
(X - 1)/2 = (y - 5)/( - 1)
Bentuk Umum Persamaan Garis
Ini dikenal sebagai bentuk umum garis dalam bidang XY ke persamaan bahwa struktur berikut memiliki:
A⋅x + b⋅y = c
Ekspresi bentuk simetris dapat ditulis ulang sehingga memiliki bentuk umum:
B⋅x - a⋅y = b⋅xo - a⋅o
Dibandingkan dengan bentuk umum dari garis tetap:
A = b, b = -a dan c = B⋅xo - A⋅o
Contoh 3
Temukan bentuk umum dari garis yang sutradara adalah u = (2, -1)
Dan apa yang melewati titik p = (1, 5).
Untuk menemukan bentuk umum, kita dapat menggunakan rumus yang diberikan, namun jalur alternatif akan dipilih.
Kita mulai dengan menemukan vektor ganda vektor U, didefinisikan sebagai vektor yang diperoleh dengan menukar komponen U dan mengalikan dengan -1 yang kedua:
W= (-1, -2)
Vektor ganda W sesuai dengan rotasi dalam 90 ° dalam jadwal Direktur Direktur v.
Kami melipatgandakan pendakian W dengan (X, y) dan dengan (Xo, saya) Dan kami cocok dengan:
(-1, -2) • (x, y) = (-1, -2) • (1, 5)
-X -2y = -1 -2⋅5 = -11
Akhirnya tersisa:
X + 2y = 11
Bentuk standar persamaan garis
Ini dikenal sebagai bentuk standar garis di bidang XY, yang memiliki struktur berikut:
Y = m⋅x + d
di mana m mewakili kemiringan dan intersepsi d dengan sumbu dan.
Mengingat sutradara u = (a, b) vektor, kemiringan m adalah b/a.
Dan D diperoleh dengan mengganti x dan y oleh titik XO yang diketahui, saya:
I = (b/a) xo + d.
Singkatnya, m = b/a y d = me -(b/a) xo
Perhatikan bahwa kemiringan m adalah hasil bagi di antara komponen Dan Direktur dan Komponen X yang sama.
Dapat melayani Anda: keseimbangan rotasi: rumus dan persamaan, contoh, latihanContoh 4
Temukan bentuk standar garis yang sutradara adalah u = (2, -1)
Dan apa yang melewati titik p = (1, 5).
M = -½ dan d = 5 -( -½) 1 = 11/2
Y = (-1/2) x + 11/2
Latihan terpecahkan
-Latihan 1
Temukan Direktur Vektor Garis (L) yang merupakan persimpangan bidang (π): x - y + z = 3 dan bidang (Ω): 2x + y = 1.
Kemudian tulis bentuk kontinu dari garis garis (l).
Larutan
Dari persamaan bidang (Ω) Clearance Y: y = 1 -2x
Lalu kami mengganti dalam persamaan pesawat (π):
X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x
Kemudian kami parameterisasi x, kami memilih parameterisasi x = λ
Ini berarti bahwa garis memiliki persamaan vektor yang diberikan oleh:
(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)
yang bisa ditulis ulang sebagai:
(X, y, z) = (0, 1, 4) + λ (1, -2, -3)
Dengan apa yang jelas bahwa vektor atau = (1, -2, -3) adalah vektor pengelola lurus (l).
Bentuk kontinu dari garis (l) adalah:
(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)
-Latihan 2
Mengingat bidang 5x + ke Y + 4z = 5
dan garis yang persamaannya adalah x/1 = (y-2)/3 = (z -2)/(-2)
Tentukan nilainya ke sehingga pesawat dan garisnya paralel.
Solusi 2
Vektor N = (5, a, 4) adalah vektor normal ke pesawat.
Vektor atau = (1, 3, -2) adalah manajer lurus.
Jika garis sejajar dengan pesawat, maka n • v = 0.
(5, ke, 4)•(1, 3, -2) = 5 +3ke -8 = 0 ⇒ ke= 1.
Referensi
- Fleming, w., & Varberg, D. DAN. (1989). Matematika Prealculus. Prentice Hall Ptr.
- Kolman, b. (2006). Aljabar linier. Pendidikan Pearson.
- Loyal, J. M., & Viloria, n. G. (2005). Geometri analitik datar. Mérida - Venezuela: Editorial Venezuela C. KE.
- Navarro, Rocio. Vektor. Dipulihkan dari: Buku.Google.bersama.pergi.
- Pérez, c. D. (2006). Prequalculus. Pendidikan Pearson.
- Prenowitz, w. 2012. Konsep dasar geometri. Rowman & Littlefield.
- Sullivan, m. (1997). Prequalculus. Pendidikan Pearson.