Vektor kolineal

Kami menjelaskan apa itu vektor colineal, sistem vektor colineal dan kami memberikan beberapa contoh

Apa saja vektor kolineal?

Itu Vektor kolineal Mereka adalah salah satu dari tiga jenis vektor yang ada. Ini adalah vektor -vektor yang berada dalam arah atau garis aksi yang sama. Ini berarti yang berikut ini: Dua atau lebih vektor akan menjadi kolineal jika ada kasus bahwa mereka diatur dalam garis yang sejajar satu sama lain.

Vektor didefinisikan sebagai besarnya diterapkan pada tubuh dan ditandai dengan memiliki arah, rasa dan skala. Vektor dapat ditemukan di pesawat atau di ruang angkasa dan dapat dari berbagai jenis: vektor kolineal, vektor bersamaan dan vektor paralel.

Kapan ada vektor kolineal?

Vektor adalah kolineal jika garis aksi satu adalah garis aksi yang persis sama dari semua vektor lainnya, terlepas dari ukuran dan arah masing -masing vektor.

Vektor digunakan sebagai representasi di berbagai bidang seperti matematika, fisika, aljabar dan juga dalam geometri, di mana vektor hanya kolineal ketika arahnya sama, terlepas dari bahwa artinya tidak.

Contoh vektor colineal

• Dua atau lebih vektor adalah kolineal jika hubungan antara koordinat adalah sama.

Contoh 1

Anda memiliki vektor m = m_x; m_y dan n = n_x; N_. Ini adalah collinear jika:

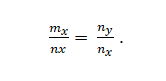
Contoh 2

Dapat ditentukan jika vektor j = 3,6,15 dan p = 1,2,5 adalah collinear melalui hubungan koordinat mereka, yang Anda harus sebanding satu sama lain; artinya: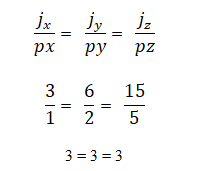

• Dua atau lebih vektor adalah kolineal jika multiplikasi produk atau vektor sama dengan nol (0). Ini karena, dalam sistem koordinat, setiap vektor ditandai dengan koordinat masing -masing, dan jika ini sebanding dengan satu sama lain, vektor akan dikumpulkan. Ini dinyatakan sebagai berikut:

Dapat melayani Anda: set yang setara: apa itu, penjelasan, contoh

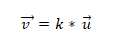
Contoh 1

Anda memiliki vektor a = (10, 5) dan b = (6, 3). Untuk menentukan apakah mereka kolineal, teori penentu diterapkan, yang menetapkan kesetaraan produk silang. Dengan cara ini, Anda harus:

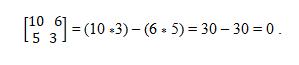
Sistem Vektor Colineal

Vektor colineal diwakili secara grafis menggunakan arah dan arah ini - dengan mengingat bahwa ini harus melalui titik aplikasi - dan modul, yang merupakan skala atau panjang tertentu.

Sistem vektor colineal terbentuk ketika dua atau lebih vektor bertindak pada objek atau tubuh, yang mewakili kekuatan dan bertindak dalam arah yang sama.

Misalnya, jika dua kekuatan kolineal diterapkan pada tubuh, yang dihasilkannya hanya akan tergantung pada pengertian di mana mereka bertindak. Ada tiga kasus, yaitu:

Vektor kolineal dengan indera yang berlawanan

Hasil dari dua vektor kolineal sama dengan jumlah ini:

R = ∑ f = f₁ + F_2.

Contoh

Jika dua kekuatan F bertindak dengan kereta₁ = 40 n dan f₂ = 20 N di arah yang berlawanan (seperti yang ditunjukkan pada gambar), hasilnya adalah:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

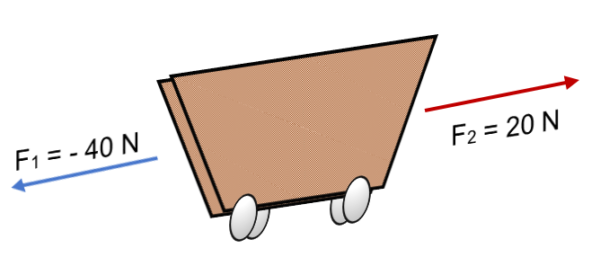Tanda negatif mengungkapkan bahwa tubuh akan bergerak ke kiri, dengan gaya yang setara dengan 20 N.

Vektor kolineal dalam arti yang sama

Besarnya gaya yang dihasilkan akan sama dengan jumlah vektor colineal:

R = ∑ f = f₁ + F_2.

Contoh

Jika dua kekuatan F bertindak dengan kereta₁ = 35 n dan f₂ = 55 N dalam arah yang sama (seperti yang ditunjukkan pada gambar), hasilnya adalah:

R = ∑ f = 35 n + 55n.

R = 90 n.

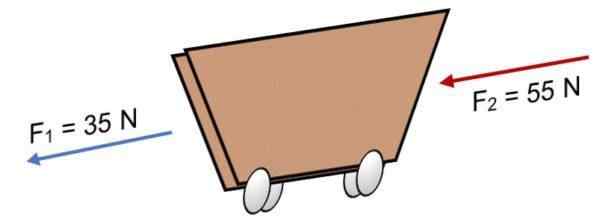
Hasil positif menunjukkan bahwa vektor collineal bertindak ke kiri.

Itu dapat melayani Anda: aturan t: karakteristik, sehingga itu, contoh

Vektor kolineal dengan besaran yang sama dan indera yang berlawanan

Hasil dari dua vektor kolineal akan sama dengan jumlah vektor collinear:

R = ∑ f = f₁ + F_2.

Karena kekuatan memiliki besarnya yang sama tetapi dalam arah yang berlawanan -yaitu, yang satu akan positif dan negatif lainnya -, dengan menambahkan kedua kekuatan hasilnya akan sama dengan nol.

Contoh

Jika dua kekuatan F bertindak dengan kereta₁ = -7 n dan f₂ = 7 n, yang memiliki besarnya sama, tetapi di arah yang berlawanan (seperti yang ditunjukkan pada gambar), hasilnya adalah:

R = ∑ f = (-7 n) + 7n.

R = 0.

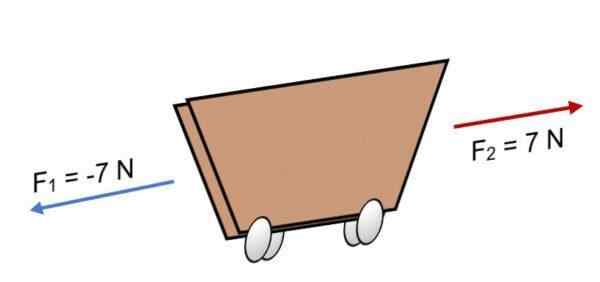
Karena hasilnya sama dengan 0, itu berarti bahwa vektor keseimbangan satu sama lain dan, oleh karena itu, tubuh seimbang atau istirahat (tidak akan bergerak).

Perbedaan antara vektor colineal dan bersamaan

Vektor colineal ditandai dengan memiliki arah yang sama pada garis yang sama, atau karena mereka sejajar dengan garis; Yaitu, mereka adalah vektor sutradara garis paralel.

Untuk bagian mereka, vektor bersamaan didefinisikan karena mereka berada di garis aksi yang berbeda yang dicegat pada satu titik.

Dengan kata lain, mereka memiliki titik asal atau kedatangan yang sama -terlepas dari modul mereka, makna atau arah -yang membentuk sudut di antara mereka.

Sistem vektor bersamaan diselesaikan dengan metode matematika atau grafik, yang merupakan metode jajaran genjang kekuatan dan metode poligon gaya. Melalui ini, nilai vektor yang dihasilkan akan ditentukan, yang menunjukkan arah di mana tubuh akan bergerak.

Pada dasarnya, perbedaan utama antara vektor collinear dan bersamaan adalah garis aksi di mana mereka bertindak: collineals bertindak dalam baris yang sama, sedangkan yang bersamaan dalam hal yang berbeda.

Dapat melayani Anda: Sistem Persamaan: Metode Solusi, Contoh, Latihan

Artinya, vektor collinear bertindak dalam satu bidang, "x" atau "y"; Dan tindakan bersamaan di kedua pesawat, mulai dari titik yang sama.

Vektor colineal tidak pada satu titik, seperti yang dilakukan secara bersamaan, karena mereka sejajar satu sama lain.

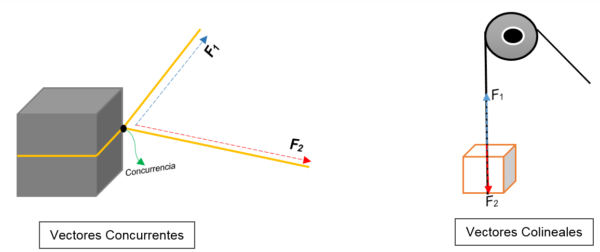
Di gambar kiri Anda dapat melihat blok. Itu diikat dengan tali dan simpul membaginya menjadi dua; Saat ditemukan menuju orientasi yang berbeda dan dengan kekuatan yang berbeda, blok akan bergerak ke arah yang sama.

Dua vektor diwakili pada satu titik (blok), terlepas dari modul, arah atau arahnya.

Di sisi lain, di gambar kanan muncul katrol yang mengangkat kotak. Tali mewakili garis tindakan; Saat dihentikan, dua kekuatan (vektor) bertindak di atasnya: gaya tegang (saat memanjat blok) dan gaya lain, yang memberikan bobot blok. Keduanya memiliki arah yang sama, tetapi dalam pengertian yang berlawanan; Mereka tidak setuju pada satu titik.