Definisi, Kondisi, Latihan Vektor Non -Coplanar

Itu Vektor non -coplanares Mereka adalah mereka yang tidak berbagi pesawat yang sama. Dua vektor bebas dan satu titik menentukan satu bidang. Vektor ketiga mungkin atau mungkin tidak berbagi pesawat itu dan jika tidak, ini adalah vektor non -coplanar.

Vektor non -couplet tidak dapat diwakili dalam dua ruang -dimensi seperti papan atau selembar kertas, karena beberapa di antaranya terkandung dalam dimensi ketiga. Untuk mewakili mereka dengan benar, Anda harus menggunakan perspektif.

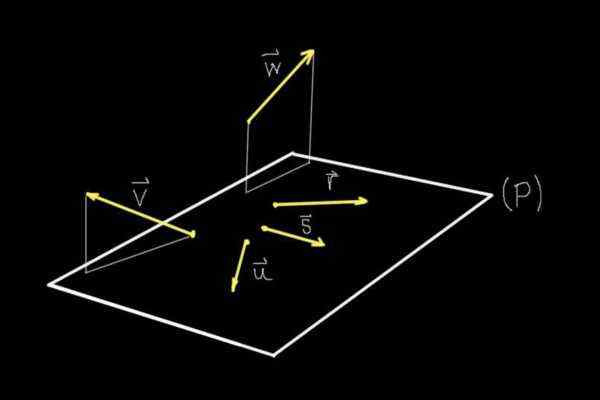
Gambar 1. Coplanares dan vektor non-kopling. (Elaborasi sendiri)

Jika kita mengamati Gambar 1, semua objek yang ditampilkan secara ketat berada di bidang layar, namun berkat perspektif otak kita dapat membayangkan sebuah pesawat (P) yang keluar dari hal yang sama.

Di pesawat itu (P) adalah vektor R, S, atau, sementara vektor v Dan W  Mereka tidak berada di pesawat itu.

Oleh karena itu vektor R, S, atau Mereka adalah coplanarios atau coplanares satu sama lain karena mereka berbagi bidang yang sama (p). Vektor v Dan W Mereka tidak berbagi flat dengan vektor lain yang ditampilkan, oleh karena itu mereka tidak berpasangan. 

[TOC]

Vektor persamaan coplanares dan pesawat

Pesawat didefinisikan secara unik jika tiga titik diberikan dalam ruang tiga dimensi.

Misalkan ketiga poin itu adalah intinya KE, titik B dan intinya C yang mendefinisikan pesawat (P). Dengan poin -poin ini dimungkinkan untuk membangun dua vektor AB = U Dan Ac = v yang merupakan konstruksi dengan pesawat (P).

Produk vektor (atau silang produk) dari kedua vektor ini menghasilkan vektor tegak lurus (atau normal) ketiga bagi mereka dan karenanya tegak lurus terhadap bidang (P):

n = u X v   => N ⊥ atau  Dan N ⊥ v   => N ⊥ (P)    

Dapat melayani Anda: berat (fisik): perhitungan, unit, contoh, latihan

Poin lain yang menjadi milik pesawat (P) harus memenuhi vektor itu Aq Jadilah tegak lurus terhadap vektor N; Ini setara dengan mengatakan bahwa produk skalar (atau produk titik) dari N dengan Aq Itu pasti nol:

N • Aq = 0 (*)

Kondisi sebelumnya setara dengan mengatakan itu:

Aq • (atau X v) = 0 

Persamaan ini memastikan intinya Q milik pesawat (P). 

Persamaan Pesawat Cartesian

Persamaan sebelumnya dapat ditulis dengan cara Cartesian. Untuk ini kami menulis koordinat poin KE, Q dan komponen vektor normal N:

A = (a, b, c)

Q = (x, y, z)

N= (NX, NY, NZ)

Sehingga komponen AQ adalah:

Aq= (X-a, y-b, z-c)

Kondisi untuk vektor Aq terkandung di pesawat (P) Ini adalah kondisi (*) yang sekarang ditulis seperti ini:

(NX, NY, NZ) • (x-a, y-b, z-c) = 0

Menghitung produk titik tetap:

nx (x-a) + ny (y-b) + nz (z-b) = 0

Jika berkembang dan mengatur ulang itu tetap:

NX X + NY Y + NZ Z = NX A + NY B + NZ C

Ekspresi sebelumnya adalah persamaan pesawat Cartesian (P), tergantung pada komponen vektor normal (P) dan koordinat suatu titik KE yang termasuk dalam (P).

Kondisi untuk tiga vektor menjadi non -coplanares

Karena kondisinya telah terlihat di bagian sebelumnya Aq • (atau X v) = 0 menjamin bahwa vektor Aq Itu adalah coplanario a atau Dan v.

Jika kita menelepon W ke vektor Aq Maka kita bisa menegaskan itu:

W, atau Dan v Mereka adalah coplanares, ya dan hanya jika W • ( atau X v ) = 0.

Kondisi non-perilaku

Jika produk triple (atau produk campuran) dari tiga vektor berbeda dari nol maka ketiga vektor tersebut bukan penutup.

Itu dapat melayani Anda: Proses Politropik: Karakteristik, Aplikasi dan Contoh

Ya    W • ( atau X v ) ≠ 0 maka vektor u, v, dan w adalah non-koplanario.

Jika komponen Cartesian dari U, V, V, dan W diperkenalkan, kondisi non-perilaku dapat ditulis sebagai berikut:

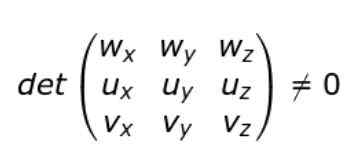Artinya jika penentu matriks (3 × 3) yang barisnya adalah komponen vektor U, V dan W maka vektor tidak kopling.

Produk rangkap tiga memiliki interpretasi geometris dan mewakili volume paralelepiped yang dihasilkan oleh tiga vektor non -coplanares.

Gambar 2. Tiga vektor non-kopling menentukan paralelepipedo yang volumenya adalah modul produk triple. (Elaborasi sendiri)

Alasannya adalah sebagai berikut; Ketika dua vektor non-kopling berlipat ganda. 

Kemudian saat vektor ini berlipat ganda. 

Dengan kata lain, Anda memiliki area jajaran genjang yang dihasilkan oleh dua yang pertama dikalikan dengan ketinggian vektor ketiga.

Kondisi alternatif non-kopling

Jika Anda memiliki tiga vektor dan salah satu dari mereka tidak dapat ditulis sebagai kombinasi linier dari dua lainnya, maka ketiga vektor itu bukan penutup. Itu adalah tiga vektor atau, v Dan W Mereka tidak ada penutup jika kondisinya:

α atau + β v + γ W = 0

Itu terpenuhi hanya ketika α = 0, β = 0 dan γ = 0.

Latihan terpecahkan

-Latihan 1

Anda memiliki tiga vektor

atau = (-3, -6, 2);   v = (4, 1, 0) dan W = (-1, 2, z)

Perhatikan bahwa komponen z vektor W Itu tidak diketahui.

Temukan kisaran nilai yang dapat diambil Z sehingga dijamin bahwa ketiga vektor tidak berbagi bidang yang sama.

Dapat melayani Anda: keseimbangan stabil: konsep dan contoh

Larutan 

Kami menerapkan lagi kriteria penentu matriks yang dibentuk oleh jajaran tiga vektor, dengan cara ini kami tetap: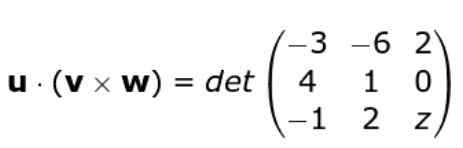Kami mengembangkan penentu

W • ( atau X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18

Kami mencocokkan ekspresi ini dengan nilai nol

21 z + 18 = 0

dan kami membersihkan z

Z = -18/21 = -6/7

Jika variabel z mengambil nilai -6/7 maka tiga vektor akan menjadi coplanares.

Sehingga nilai-nilai z yang menjamin bahwa vektor adalah non-penutup adalah nilai yang dalam interval berikut:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Latihan 2

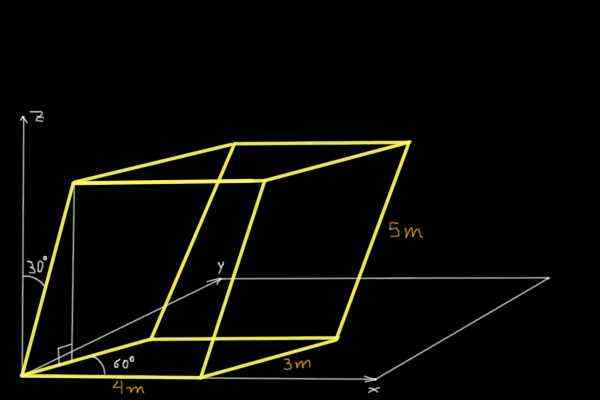
Temukan volume paralelepiped yang ditunjukkan pada gambar berikut:

Larutan 

Untuk menemukan volume paralelepiped yang ditunjukkan pada gambar, komponen Cartesian dari tiga vektor non-kopling non-konkuren akan ditentukan dalam asal sistem koordinat. Yang pertama adalah vektor atau  4m dan sejajar dengan sumbu x:

atau= (4, 0, 0) m

Yang kedua adalah vektor v Dalam bidang ukuran 3m XY yang membentuk 60º dengan sumbu x:

v= (3*cos 60º, 3*sen 60º, 0) = (1.5, 2.6, 0.0) m

Dan yang ketiga vektor W 5m dan proyeksi yang dalam bidang XY membentuk 60º dengan sumbu x, di samping itu membentuk 30º dengan sumbu z.

W= (5*sin 30º*cos 60º, 5*sen 30º*sin 60º, 5*sen 30º)

Melakukan perhitungan yang kami miliki: W= (1.25, 2.17, 2.5m.

Referensi

1. Figueroa, d. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. 31-68.
2. Fisik. Modul 8: Vektor. Dipulihkan dari: FRTL.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanika untuk Insinyur. Statis. Edisi ke -6. Perusahaan Editorial Kontinental.28-66.
4. McLean, w. Seri Schaum. Mekanika untuk Insinyur: Statis dan Dinamis. Edisi ke -3. Bukit McGraw. 1-15.
5. Wikipedia. Vektor. Pulih dari: itu.Wikipedia.org