X kuadrat

Kami menjelaskan apa yang dimaksud x kuadrat, sifatnya, contoh dan latihan diselesaikan

Area persegi sisi "X" adalah x kuadrat. Sumber: f. Zapata.

Operasi aljabar "X kuadrat"Ini dilakukan dengan mengalikan jumlah" x "dengan dirinya sendiri dua kali. Ini adalah bagian dari operasi potensiasi, dan dalam simbol matematika, itu diekspresikan dengan cara ini:

x ∙ x = x²

Ini adalah kasus khusus pemberdayaan, di mana "x" mewakili basis Dan "2" adalah eksponen. Jika dalam operasi istilah x muncul², Itu dibaca justru sebagai "x kuadrat" atau "x persegi terangkat".

Secara alami, eksponen lain dimungkinkan, misalnya, jika eksponen adalah 3, maka kekuatan ditulis sebagai:

x ∙ x ∙ x = x³

Dan baca sebagai "X to the Three", "X diangkat ke kubus" atau sekadar "X ke kubus".

Secara umum, eksponen tempat pangkalannya tinggi dapat berupa angka apa saja, yang disebut "n" dan dalam hal ini, kekuatan yang sesuai ditulis:

X^N = x ∙ x ∙ x ∙… ∙ x

Di sini poin suspensi menunjukkan bahwa "x" harus dikalikan dengan sendirinya "n", yaitu, sebanyak eksponen menunjukkannya.

Beberapa contoh sederhana "x kuadrat", dengan angka, adalah sebagai berikut:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Nanti, berbagai aplikasi dijelaskan yang perlu.

Sifat potensiasi

Secara umum, produk dari jumlah berapa pun dengan dirinya sendiri, n kali, itu disebut potensiasi. Perhitungan x kuadrat hanyalah kasus potensiasi tertentu, dua kasus lain muncul ketika Anda ingin menaikkan jumlah ke eksponen 1, memperoleh sebagai hasilnya jumlah yang sama:

Dapat melayani Anda: hukum eksponen

Karena operasi ini sering, untuk bekerja dengan basis dan eksponen, beberapa aturan operasi sederhana diikuti, disebut Hukum eksponen, yang tercantum di bawah ini:

Hukum eksponen

Berikut ini, "X" adalah basis dan "n" dan "m" adalah eksponen.

1.- Produk kekuatan dasar yang sama

Dengan mengalikan dua (atau lebih) kekuatan dengan dasar yang sama, basis yang ditingkatkan dengan jumlah eksponen diperoleh:

X^N∙ x^M = x^n+m

Dalam kasus X tinggi, aturan ini diterapkan sebagai berikut, menggantikan N dan M untuk 1:

X¹∙ x¹ = x¹⁺¹ = x²

2.- Powers Divisi dengan basis yang sama

Dengan membagi kekuatan pangkalan yang sama, pangkalan diperoleh, dinaikkan ke pengurangan antara masing -masing eksponen pembilang dan penyebut:

X^N ÷ x^M = x^N-m

Karena divisi oleh 0 tidak didefinisikan, itu harus dipenuhi dengan ketentuan bahwa x ≠ 0.

3.- Kekuatan Kekuatan

Hasil kekuatan suatu kekuatan sama dengan basis yang ditinggikan ke produk eksponen:

(X^M)^N = x^M∙N

Itu dapat diperoleh lagi x square, saat melakukan m = 1 dan n = 2:

(X¹)² = x^1∙2 = x²

4.- Eksponen negatif

Untuk eksponen negatif, operasi yang akan dilakukan adalah:

Setiap kali x ≠ 0. Perhatikan bahwa, dalam hal ini, daya menjadi fraksi dengan pembilang yang sama dengan 1.

5.- Eksponen fraksional

Eksponen fraksional dapat ditulis sebagai akar ke -n dari pangkalan:

Dengan syarat bahwa n berbeda dari 0. Nilai ini menjadi indeks root, sedangkan m menjadi eksponen kuantitas di bawah root, yang dalam hal ini adalah x.

Dapat melayani Anda: apa pedomannya? (Geometri)

Produk dan Quotients dari Basis yang Berbeda

Ketika Anda harus meningkatkan produk dan quotients dari pangkalan "X" dan "Y" yang berbeda, aturan ini diikuti:

1.- Daya produk

Untuk melakukan kekuatan ini, setiap jumlah dinaikkan ke eksponen N dan produk yang dihasilkan ditetapkan:

(x ∙ y)^N = x^N ⋅ dan^N

2.- Rasio hasil bagi

Sekali lagi, setiap jumlah harus dinaikkan ke eksponen n secara terpisah dan menetapkan hasil bagi hasilnya, mengikuti aturan bahwa jumlah "y" berbeda dari 0, dalam kasus positif "n": positif:

(x ÷ y)^N = x^N ÷ y^N

Ketika "n" negatif, kehati -hatian harus diambil, karena properti 4 dari bagian sebelumnya, pembilang menjadi penyebut. Dalam hal ini, kedua jumlah tersebut harus berbeda dari 0, karena divisi dengan 0 harus dihindari di semua biaya.

Contoh

Contoh 1: Kotak bilangan alami

Kotak dari sepuluh angka alami pertama adalah:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Contoh 2: kuadrat angka negatif

Kuadrat dari angka negatif selalu positif, karena dua jumlah tanda yang sama dikalikan, oleh karena itu: oleh karena itu:

(-x) · (-x) = x ∙ x = x²

Misalnya:

(-2) · (-2) = (-2)² = 4

Contoh 3: kuadrat dari jumlah dan perbedaan

Seringkali perlu untuk menghitung kuadrat dari jumlah dua kuantitas, atau perbedaannya, operasi yang termasuk dalam kategori produk terkenal.

Operasi diselesaikan dengan indikasi yang diberikan dan bantuan properti distributif:

Kuadrat dari jumlah

Biarkan dua "x" dan "y" jumlah, dan Anda ingin menemukan kuadrat dari jumlahnya (x + y)²:

Dapat melayani Anda: hierarki operasi

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + dan²

Ekspresi ini berbunyi seperti ini: "kuadrat yang pertama, ditambah produk ganda yang pertama untuk yang kedua ditambah kuadrat yang kedua".

Persegi perbedaan

Itu diselesaikan secara analog, tetapi dengan mempertimbangkan tanda negatif:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ dan + dan²

Contoh 4: Area persegi

Kotak adalah poligon 4 -sided, yang memiliki ukuran yang sama. Biarkan ℓ menjadi pengukuran samping, lalu area A dari gambar diberikan oleh:

A = ℓ²

Contoh 5: Teorema Pythagoras

Teorema ini berlaku untuk segitiga persegi panjang, yang di mana dua sisi membentuk sudut lurus. Sisi ini dikenal sebagai "kategori" dan sisi yang tersisa adalah "hypotenuse".

Teorema menetapkan bahwa kuadrat hipotenusa sama dengan jumlah kotak kategori. Menyebut "A" dan "B" ke kategori, dan "C" ke hipotenuse, teorema ditulis sebagai:

C² = a² + B²

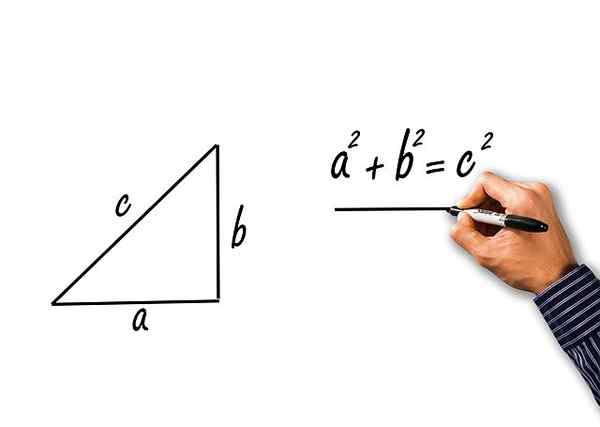Teorema Pythagoras untuk segitiga persegi panjang kucing A dan B, dan hypotenusa C

Latihan terpecahkan

Latihan 1

Hitung kuadrat hipotenus yang kakinya berukuran 3 dan 5 unit.

Larutan

Menurut teorema Pythagoras, kuadrat hipotenuse adalah:

C² = a² + B²

Mengganti nilainya:

C² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Latihan 2

Tentukan luas persegi samping ℓ = 6 cm

Larutan

A = ℓ² = (6 cm)² = 36 cm²