Definisi percepatan sentripetal, rumus, perhitungan, latihan

Itu percepatan sentripetal ke_C, Juga disebut radial atau normal, akselerasi yang membawa objek seluler saat menggambarkan lintasan melingkar. Besarnya v²/R, Di mana R Ini adalah jari -jari lingkaran, diarahkan ke pusatnya dan bertanggung jawab atas ponsel untuk tetap di rutenya.

Dimensi akselerasi sentripetal adalah panjang per satuan waktu. Dalam sistem internasional mereka adalah m/s². Jika karena alasan tertentu akselerasi sentripetal menghilang, demikian pula kekuatan yang memaksa ponsel untuk mempertahankan lintasan melingkar.

Objek berputar memiliki akselerasi sentripetal, yang diarahkan ke pusat lintasan. Sumber: Pixabay

Inilah yang terjadi pada mobil yang mencoba memberikan kurva di jalur datar dan salju, di mana gesekan antara lantai dan roda tidak cukup sehingga mobil mengambil kurva. Oleh karena itu satu -satunya kemungkinan yang tersisa adalah bergerak dalam garis lurus dan itulah sebabnya Anda keluar dari kurva.

[TOC]

Gerakan melingkar

Ketika suatu objek bergerak dalam lingkaran, setiap saat akselerasi sentripetal diarahkan secara radial ke arah pusat keliling, arah yang tegak lurus terhadap lintasan diikuti.

Karena kecepatan selalu bersinggungan dengan lintasan, maka kecepatan dan akselerasi sentripetal berubah menjadi tegak lurus. Oleh karena itu kecepatan dan akselerasi tidak selalu memiliki arah yang sama.

Dalam keadaan ini, ponsel memiliki kemungkinan menggambarkan keliling dengan kecepatan konstan atau variabel. Kasing pertama dikenal sebagai gerakan melingkar seragam atau MCU dengan akronimnya, kasus kedua akan menjadi gerakan melingkar variabel.

Itu bisa melayani Anda: apa penghapusan emisinya? (Dengan contoh)

Dalam kedua kasus tersebut, akselerasi sentripetal bertanggung jawab untuk menjaga keliling ponsel, menempati bahwa kecepatan hanya bervariasi dalam arah dan arah.

Namun, untuk memiliki gerakan melingkar variabel, komponen percepatan lain dalam arah kecepatan yang sama akan diperlukan, yang bertanggung jawab untuk meningkatkan atau mengurangi kecepatan. Komponen akselerasi ini dikenal sebagai Percepatan tangensial.

Gerakan melingkar variabel dan gerakan lengkung pada umumnya memiliki kedua komponen percepatan, karena gerakan lengkung dapat membayangkan sebagai rute melalui lengkungan keliling yang tak terhitung banyaknya yang membentuk lintasan melengkung.

Gaya sentripetal

Sekarang, kekuatan bertanggung jawab untuk memberikan percepatan. Untuk satelit yang mengorbit bumi, itu adalah gaya gravitasi. Dan karena gravitasi selalu bertindak tegak lurus terhadap lintasan, itu tidak mengubah kecepatan satelit.

Dalam hal ini, gravitasi bertindak sebagai a gaya sentripetal, Bahwa itu bukan kelas khusus atau terpisah dari kekuatan, tetapi yang dalam kasus satelit, secara radial diarahkan ke pusat bumi.

Dalam jenis gerakan melingkar lain, misalnya mobil yang mengambil kurva, peran gaya sentripetal ditafsirkan oleh gaya rubb statis yang memaksa ponsel untuk berputar.

Rumus untuk percepatan sentripetal

Akselerasi sentripetal dihitung dengan ekspresi:

Ac = v²/R

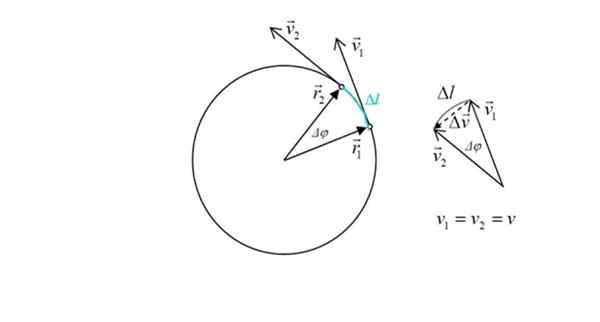Diagram untuk menghitung akselerasi sentripetal dalam ponsel dengan MCU. Sumber: Sumber: Ilevanat [CC BY-SA 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)]

Ekspresi ini akan disimpulkan di bawah ini. Menurut akselerasi definisi adalah variasi kecepatan dalam waktu:

Itu dapat melayani Anda: sumber cahaya: jenis dan perangkat yang memancarkan cahaya

Diagram teratas menunjukkan pada gambar kiri, dua titik di mana ponsel melewati yang bergerak di lingkaran radio R dalam arti anti -puaian. Perhatikan bahwa besarnya kecepatan adalah sama dalam kedua kasus, tetapi bukan arah atau makna.

Ponsel menggunakan waktu δT Dalam tur, yang kecil, karena poinnya sangat dekat.

Gambar tersebut juga menunjukkan dua vektor posisi R₁ Dan R₂, Modul yang sama: Radio R keliling. Sudut antara kedua titik adalah Δφ. Berwarna hijau busur Tur ponsel, dilambangkan sebagai Δl.

Pada gambar di sebelah kanan terlihat bahwa besarnya Δv, Perubahan kecepatan kira -kira sebanding dengan ΔL, karena sudut Δφ kecil. Tetapi perubahan kecepatan terkait dengan akselerasi. Segitiga diperingatkan, dengan jumlah vektor bahwa:

v₁ + Δv = v₂ → δV = V₂ - v₁

Δv Itu menarik, karena sebanding dengan akselerasi sentripetal. Dari gambar itu diperingatkan bahwa menjadi sudut kecil Δφ, vektor Δv Itu adalah esensi tegak lurus keduanya v₁ menyukai v₂ dan menunjuk ke pusat keliling.

Meskipun vektor menonjol dalam tebal, untuk efek sifat geometris yang mengikuti, kami bekerja dengan modul atau besarnya vektor -vektor ini, terlepas dari notasi vektor.

Sesuatu yang lain: Anda perlu menggunakan definisi sudut tengah, yaitu:

Δφ= Δl/r

Sekarang kedua angka dibandingkan, yang proporsional karena sudut δφ itu biasa:

Dapat melayani Anda: apa itu cahaya terpolarisasi?

 

Membagi antara Δt:

 Karena dengan definisi kecepatan adalah v = Δl/ Δt. Tetapi δV/ ΔT Justru besarnya akselerasi sentripetal, itulah yang dicari. Dengan cara ini ekspresi yang dijelaskan di awal tercapai:

ke_C= v²/R

Olahraga diselesaikan

Partikel bergerak dalam lingkaran 2.Radio 70 m. Pada waktu tertentu akselerasinya adalah 1.05 m/s² Ke arah yang membuat sudut 32.0º dengan Direktorat Gerakan. Hitung kecepatan Anda:

a) pada saat itu

b) 2.00 detik kemudian, dengan asumsi akselerasi tangensial konstan.

Menjawab

Ini adalah gerakan melingkar yang bervariasi, karena pernyataan tersebut menunjukkan bahwa akselerasi memiliki sudut yang diberikan dengan arah gerakan yang tidak atau 0º (tidak bisa berupa gerakan melingkar) atau 90º (itu akan menjadi gerakan melingkar yang seragam).

Oleh karena itu dua komponen - radial dan tangensial - hidup berdampingan. Akan dilambangkan sebagai_C sudah_T dan tampak ditarik pada gambar berikut. Vektor hijau adalah vektor akselerasi bersih atau hanya percepatan ke.

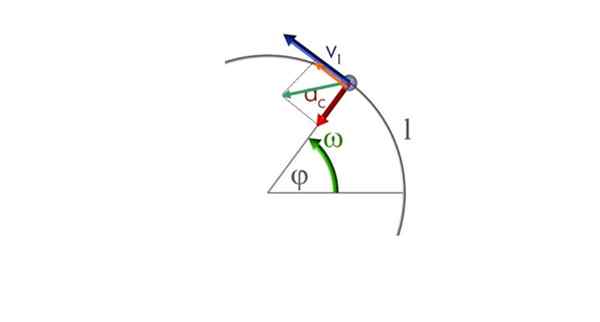Sebuah partikel bergerak dalam lintasan melingkar dalam pengertian anti -adanya dan beragam gerakan melingkar. Sumber: Commons.Wikimedia.org

a) Perhitungan komponen akselerasi

ke_C = a.cos θ = 1.05 m/s² . cos 32.0º = 0.89 m/s² (merah)

ke_T = a.sin θ = 1.05 m/s² . Sen 32.0º = 0.57 m/s² (berwarna oranye)

Perhitungan kecepatan seluler

Sejak_C = v²/R, Jadi:
b) 2 detik kemudian kecepatan v akan ditingkatkan berkat komponen tangensial percepatan

V = V_{salah satu} +ke_T. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Referensi

1. Giancoli, d. Fisika. 2006. Prinsip dengan aplikasi. Edisi Keenam. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Ilmu Fisik Konseptual. Edisi Kelima.Pearson.106 - 108.