Data yang tidak dikelompokkan contoh dan olahraga diselesaikan

Itu Data yang tidak dikelompokkan Mereka adalah mereka yang, diperoleh dari sebuah penelitian, belum diatur oleh kelas. Ketika jumlah data yang dapat dikelola, biasanya 20 atau kurang, dan ada beberapa data yang berbeda, mereka dapat diperlakukan sebagai tidak dikelompokkan dan mengekstrak informasi berharga dari mereka.

Data yang tidak dikelompokkan berasal dari survei atau penelitian yang dilakukan untuk mendapatkannya dan karenanya kurang diproses. Mari kita lihat beberapa contoh:

Gambar 1. Data yang tidak dikelompokkan datang langsung dari studi apa pun dan belum diklasifikasikan. Sumber: Pxhere.

-Hasil ujian CI koefisien intelektual pada 20 siswa acak dari universitas. Data yang diperoleh adalah sebagai berikut:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112.106

-Usia 20 karyawan dari kafetaria yang sangat populer:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

-Catatan akhir rata -rata 10 siswa dari kelas matematika:

3.2; 3.1; 2,4; 4.0; 3.5; 3.0; 3.5; 3.8; 4.2; 4.9

[TOC]

Properti Data

Ada tiga sifat penting yang menjadi ciri sekumpulan data statistik dikelompokkan atau tidak, yaitu:

-Posisi, yang merupakan kecenderungan data yang akan dikelompokkan di sekitar nilai -nilai tertentu.

-Penyebaran, Indikasi seberapa tersebar atau disebarluaskan adalah data di sekitar nilai tertentu.

-Membentuk, Itu mengacu pada cara di mana data didistribusikan, yang dapat dilihat ketika grafiknya dibangun. Ada kurva yang sangat simetris dan bias, baik di sebelah kiri atau di sebelah kanan dari nilai sentral tertentu.

Untuk masing -masing properti ini ada sejumlah langkah yang menggambarkannya. Setelah diperoleh, mereka memberi kita panorama perilaku data:

-Ukuran posisi yang paling banyak digunakan adalah rata -rata aritmatika atau sekadar sedang, median dan mode.

-Dalam dispersi rentang, varians dan standar deviasi sering digunakan, tetapi mereka bukan satu -satunya langkah dispersi.

Dapat melayani Anda: homotecia

-Dan untuk menentukan bentuknya, rata -rata dan median dibandingkan melalui bias, seperti yang akan dilihat segera.

Perhitungan rata -rata, median dan mode

-Rata -rata aritmatika, Juga dikenal sebagai rata -rata dan dilambangkan sebagai x, dihitung sebagai berikut:

X = (x₁ + X₂ + X₃ +... X_N) / N

Dimana x₁, X₂,.. . X_N, adalah data dan n adalah total dari mereka. Di penjumlahan jumlah ada:

Di sini indeks saya mewakili data 1, data 2, data 3 dan seterusnya, sampai mencapai satu -satunya, yang merupakan yang terakhir.

-Mediannya Itu adalah nilai yang muncul di tengah -tengah suksesi data yang tertib, jadi untuk mendapatkannya, perlu memesan data terlebih dahulu.

Jika jumlah pengamatannya aneh, tidak ada masalah dalam menemukan titik tengah set, tetapi jika kita memiliki sepasang data, dua data pusat dicari dan dirata -rata.

-Mode Itu adalah nilai paling umum yang diamati dalam kumpulan data. Itu tidak selalu ada, karena ada kemungkinan bahwa tidak ada nilai yang diulang lebih sering daripada yang lain. Mungkin juga ada dua data dengan frekuensi yang sama, dalam hal ini ada pembicaraan tentang distribusi bi-modal.

Berbeda dengan dua langkah sebelumnya, fashion dapat digunakan dengan data kualitatif.

Mari kita lihat bagaimana langkah -langkah posisi ini dihitung dengan contoh:

Contoh terpecahkan

Misalkan Anda ingin menentukan rata -rata aritmatika, median dan mode dalam contoh yang diusulkan di awal: usia 20 karyawan kafetaria:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

Itu setengah Itu dihitung hanya dengan menambahkan semua nilai dan membagi dengan n = 20, yang merupakan jumlah total data. Cara ini:

Dapat melayani Anda: Hubungan Proporsionalitas: Konsep, Contoh dan Latihan

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 tahun.

Untuk menemukan median Perlu memesan kumpulan data terlebih dahulu:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Seperti beberapa data, dua data pusat, disorot dengan huruf tebal, diambil, dan dirata -rata. Karena keduanya 22, mediannya adalah 22 tahun.

Akhirnya, mode Itu adalah fakta yang paling diulang atau yang frekuensinya lebih besar, menjadi 22 tahun ini.

Rentang, varians, standar deviasi dan bias

Kisarannya hanyalah perbedaan antara jurusan dan yang paling sedikit dari data dan memungkinkan variabilitas mereka untuk dengan cepat menghargai. Namun terpisah, ada langkah -langkah dispersi lain yang menawarkan informasi lebih lanjut tentang distribusi data.

Varians dan standar deviasi

Varians dilambangkan sebagai s dan dihitung dengan ekspresi:

Ini sering bekerja dengan quasirians alih-alih varian, yang dihitung dengan cara yang sama, hanya dibagi dengan N-1, alih-alih melakukan antara N:

Karena variannya adalah jumlah kotak, hasil di kuadrat unit sampel. Misalnya, dalam studi tentang usia karyawan di kafetaria, varian akan datang dalam bertahun -tahun².

Kemudian untuk menafsirkan hasil dengan benar, standar deviasi seperti akar kuadrat dari varians, atau juga deviasi kuasi standar didefinisikan, yang merupakan akar kuadrat dari quasivariance:

Bias

Ini adalah perbandingan antara rata -rata X dan median med:

-Ya Med = Media X: Data simetris.

-Saat x> med: bias di sebelah kanan.

-Dan jika x < Med: los datos sesgan hacia la izquierda.

Olahraga diselesaikan

Temukan rata -rata, median, mode, pangkat, varian, standar deviasi dan bias untuk hasil ujian koefisien intelektual 20 siswa dari universitas:

Dapat melayani Anda: fungsi matematika

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Larutan

Kami akan memesan data, karena akan diperlukan untuk menemukan median.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

Dan kami akan menempatkan mereka di tabel sebagai berikut, untuk memfasilitasi perhitungan. Kolom kedua berjudul "Akumulasi" adalah jumlah dari data yang sesuai ditambah sebelumnya.

Kolom ini akan dengan mudah menemukan rata -rata, membagi akumulasi terakhir antara jumlah total data, seperti yang terlihat pada akhir kolom "akumulasi":

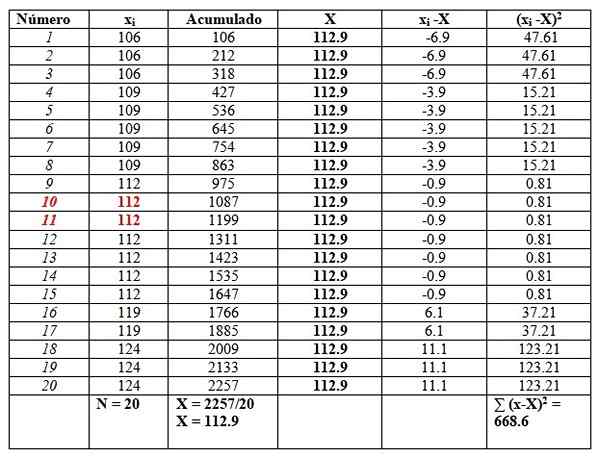
X = 112.9

Median adalah rata -rata data pusat yang disorot dalam warna merah: angka 10 dan angka 11. Seperti yang sama, mediannya adalah 112.

Akhirnya, fashion adalah nilai yang paling diulang dan 112, dengan 7 pengulangan.

Adapun langkah -langkah dispersi, rentangnya adalah:

124-106 = 18.

Varians diperoleh dengan membagi hasil akhir kolom kanan antara N:

S = 668.6/20 = 33.42

Dalam hal ini, standar deviasi adalah akar kuadrat dari varian: √33.42 = 5.8.

Di sisi lain, nilai -nilai kuasivarian dan standar deviasi kuasi adalah:

S_C= 668.6/19 = 35.2

Standar kuasi-deviasi = √35.2 = 5.9

Akhirnya, bias sedikit ke kanan, karena rata -rata 112.9 lebih besar dari median 112.

Referensi

1. Berenson, m. 1985. Statistik untuk Administrasi dan Ekonomi. Inter -American s.KE.
2. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
3. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
4. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
5. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.