Distribusi chi-square (χ²), bagaimana itu dihitung, contoh

Bukti Chi kuadrat salah satu Ji-square (χ², Di mana χ adalah surat Yunani yang disebut "chi") digunakan untuk menentukan perilaku variabel tertentu dan juga ketika Anda ingin tahu apakah dua atau lebih variabel secara statistik independen.

Untuk memeriksa perilaku suatu variabel, tes yang akan disebut Uji penyesuaian chi square. Untuk mengetahui apakah dua atau lebih variabel secara statistik independen dari tes ini disebut Chi Square of Independence, disebut juga kontingensi.

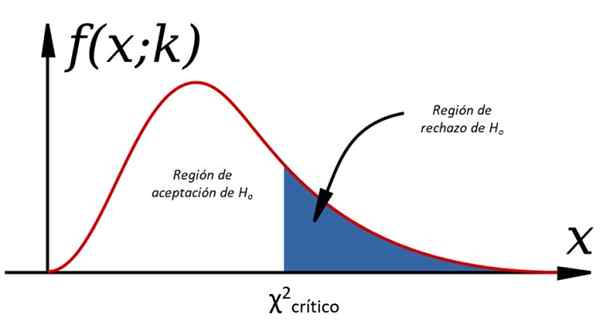
Gambar 1. Tes Hipotesis melalui Chi Cuadrado

Bukti -bukti ini adalah bagian dari teori statistik keputusan, di mana populasi dipelajari dan keputusan dibuat tentang hal itu, menganalisis satu atau beberapa sampel yang diekstraksi darinya. Untuk ini perlu membuat asumsi tertentu mengenai variabel, disebut hipotesa, mana yang mungkin atau mungkin tidak pasti.

Ada beberapa tes untuk membandingkan dugaan ini dan menentukan mana yang valid, dalam margin kepercayaan tertentu, termasuk uji chi-square, yang dapat diterapkan untuk membandingkan dua dan sebagian besar populasi.

Seperti yang akan kita lihat, dua jenis hipotesis tentang beberapa parameter populasi dalam dua sampel biasanya dipertimbangkan: hipotesis nol, yang disebut h_{salah satu} (Sampelnya independen), dan hipotesis alternatif, dilambangkan sebagai h₁, (Sampel berkorelasi) yang bertentangan dengan itu.

[TOC]

Kapan tes chi-square digunakan?

Tes Chi Square berlaku untuk variabel yang menggambarkan kualitas, seperti jenis kelamin, status sipil, kelompok darah, warna mata dan preferensi dari berbagai jenis.

Tes dirancang saat diinginkan:

-Periksa apakah distribusi yang tepat untuk menggambarkan variabel, yang disebut kebaikan penyesuaian. Melalui uji CHI Square Anda dapat mengetahui jika ada perbedaan yang signifikan antara distribusi teoritis yang dipilih dan distribusi frekuensi yang diamati.

-Tahu jika dua variabel x dan y independen dari sudut pandang statistik. Ini dikenal sebagai Tes Kemerdekaan.

Karena ini berlaku untuk variabel kualitatif atau kategorikal, uji CHI Square banyak digunakan dalam ilmu sosial, administrasi dan kedokteran.

Ketentuan untuk menerapkannya

Ada dua persyaratan penting untuk menerapkannya dengan benar:

Itu dapat melayani Anda: apa hubungan antara area belah ketupat dan persegi panjang?

-Data harus dikelompokkan dalam frekuensi.

-Sampel harus cukup besar untuk membuat distribusi chi square valid, jika tidak nilainya terlalu tinggi dan menimbulkan penolakan hipotesis nol ketika seharusnya tidak demikian.

Aturan umum adalah bahwa jika dalam data yang dikelompokkan frekuensi dengan nilai kurang dari 5 muncul, tidak digunakan. Jika ada lebih dari satu frekuensi kurang dari 5, maka mereka harus digabungkan dalam satu untuk mendapatkan frekuensi dengan nilai numerik lebih besar dari 5.

Distribusi chi square

χ² Ini adalah distribusi probabilitas yang berkelanjutan. Sebenarnya ada kurva yang berbeda, tergantung pada parameter k ditelepon derajat kebebasan secara acak.

Propertinya adalah:

-Area di bawah kurva sama dengan 1.

-Nilai χ² Mereka positif.

-Distribusinya asimetris, yaitu bias.

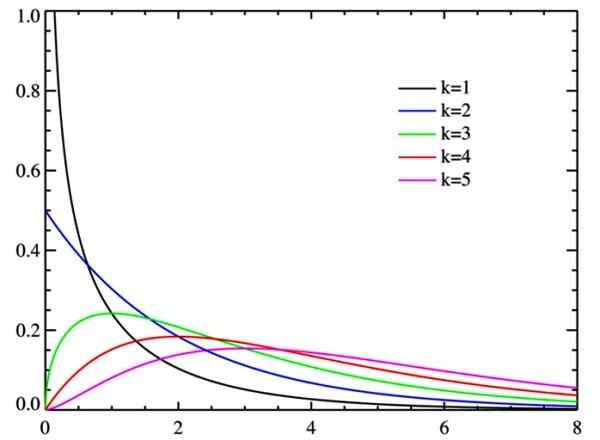Gambar 2. Distribusi chi square untuk watts derajat kebebasan. Sumber: Wikimedia Commons.

Derajat kebebasan

Ketika derajat kebebasan meningkat, distribusi chi-square cenderung normal, seperti yang dapat dilihat pada gambar.

Untuk distribusi yang diberikan, derajat kebebasan ditentukan melalui tabel kontingensi, yang merupakan tabel di mana frekuensi variabel yang diamati dicatat.

Jika ada meja F peringkat dan C kolom, nilai k adalah:

K = (f - 1) ⋅ (c - 1)

Formulasi hipotesis

Ketika uji chi square adalah penyesuaian, hipotesis berikut diformulasikan:

-H_{salah satu}: variabel x memiliki distribusi probabilitas f (x) dengan parameter spesifik dan₁, Dan₂… , Dan_P

-H₁: X memiliki distribusi probabilitas lain.

Distribusi probabilitas yang diasumsikan dalam hipotesis nol dapat, misalnya, distribusi normal yang diketahui dengan baik, dan parameternya adalah rata -rata μ dan standar deviasi σ.

Selain itu, hipotesis nol dievaluasi dengan tingkat signifikansi tertentu, yaitu, ukuran kesalahan yang akan dilakukan ketika menolaknya benar.

Secara umum, level ini ditetapkan 1 %, 5 % atau 10 % dan semakin rendah hasil tes, semakin andal.

Dapat melayani Anda: mumm

Dan jika uji kontingensi chi square digunakan, yang seperti yang kami katakan berfungsi untuk memverifikasi kemandirian antara dua variabel x dan y, hipotesisnya adalah:

-H_{salah satu}: Variabel x dan y independen.

-H₁: X dan y tergantung.

Sekali lagi perlu untuk menentukan tingkat signifikansi untuk mengetahui ukuran kesalahan saat membuat keputusan.

Bagaimana statistik chi-square dihitung?

Statistik chi square dihitung sebagai berikut:

Simbol ∑ berarti "penjumlahan", yang harus kita buat tentang ekspresi fraksional yang ditunjukkan.

Jumlah dilakukan dari kelas pertama i = 1 hingga yang terakhir, yaitu i = k.

Di samping itu:

-F_{salah satu} Ini adalah frekuensi yang diamati (berasal dari data yang diperoleh).

-F_Dan Ini adalah frekuensi yang diharapkan atau teoretis (perlu menghitungnya dari data).

Untuk menerima atau menolak hipotesis nol, χ dihitung² Untuk data yang diamati dan dibandingkan dengan nilai yang disebut CHI Kotak Kritis, yang tergantung pada tingkat kebebasan k dan tingkat signifikansi α:

χ²_kritis =  χ²_{K, α}

Jika, misalnya, kami ingin melakukan tes dengan tingkat signifikansi 1 %, maka α = 0.01, jika akan dengan 5% maka α = 0.05 dan seterusnya. P, parameter distribusi, seperti:

P = 1 - α

Nilai kuadrat kritis ini ditentukan oleh tabel yang berisi nilai area yang terakumulasi. Misalnya, untuk k = 1, yang mewakili 1 derajat kebebasan dan α = 0.05, setara dengan p = 1-.05 = 0.95, nilai χ² Itu 3.841.

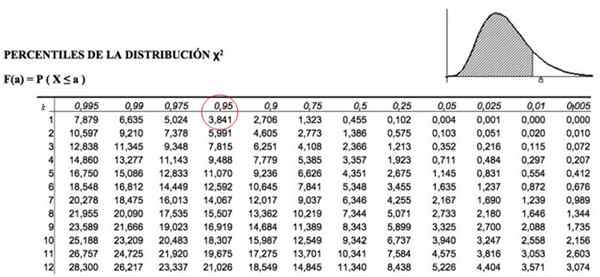Gambar 3. Tabel nilai distribusi chi square. Sumber: f. Zapata.

Kriteria penerimaan AC_{salah satu}

Kriteria untuk menerima h_{salah satu} adalah:

-Ya χ² < χ²_kritis  H_{salah satu}, Kalau tidak ditolak (lihat Gambar 1).

Contoh perhitungan

Dalam aplikasi berikut, uji CHI Square akan digunakan sebagai tes independensi.

Asumsikan bahwa para peneliti ingin tahu apakah preferensi untuk kopi hitam terkait dengan genre orang tersebut, dan menentukan jawaban dengan tingkat signifikansi α = 0.05.

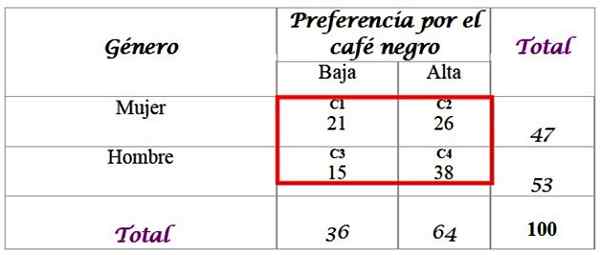
Dapat melayani Anda: sudut alternatif eksternal: latihan dan latihan diselesaikan

Untuk ini, sampel 100 orang yang diwawancarai dan jawaban mereka tersedia:

Langkah 1

Menetapkan hipotesis:

-H_{salah satu}: jenis kelamin dan preferensi untuk kopi hitam mandiri.
-H₁: Rasa untuk kopi hitam terkait dengan genre orang tersebut.

Langkah 2

Hitung frekuensi yang diharapkan untuk distribusi, di mana total ditambahkan di baris terakhir dan di kolom kanan -sayap diperlukan. Setiap sel dalam kotak merah memiliki nilai yang diharapkan F_Dan, yang dihitung dengan mengalikan total baris R -nya F dengan total kolom C, dibagi dengan total sampel n:

F_Dan = (F x c) /n

Hasilnya adalah sebagai berikut untuk setiap sel:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Langkah 3

Maka Anda harus menghitung statistik Chi Cuadrado untuk distribusi ini, menurut formula yang diberikan:

χ²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Langkah 4

Tentukan χ²_kritis, Mengetahui bahwa data yang terdaftar berada pada f = 2 baris dan c = 2 kolom, oleh karena itu, jumlah derajat kebebasan adalah:

K = (2-1) ⋅ (2-1) = 1.

Yang berarti bahwa kita harus melihat pada tabel yang ditunjukkan di atas nilai χ²_{K, α} = χ²_{1; 0.05} , yang:

χ²_kritis = 3.841

Langkah 5

Bandingkan nilai -nilainya dan putuskan:

χ² = 2.9005

χ²_kritis = 3.841

Sejak χ² < χ²_kritis Hipotesis nol diterima dan disimpulkan bahwa preferensi untuk kopi hitam tidak terkait dengan genre orang tersebut, dengan tingkat signifikansi 5%.

Referensi

1. Uji chi square untuk kemerdekaan. Pulih dari: saylordotorg.GitHub.Io.
2. Gelombang med. Statistik diterapkan pada ilmu kesehatan: Tes Ji-Square. Pulih dari: medwave.Cl.
3. Probabilitas dan statistik. Tes kebaikan penyesuaian shi square. Diperoleh dari: Probabilitas dan Estics.com.
4. Triola, m. 2012. Statistik dasar. 11. Edisi. Addison Wesley.
5. Unam. Tes Chi Square. Dipulihkan dari: Penasihat.Cuautitlan2.Unam.MX.