Contoh data yang dikelompokkan dan latihan terselesaikan

Itu data yang dikelompokkan Mereka adalah mereka yang telah diklasifikasikan ke dalam kategori atau kelas, mengambil kriteria frekuensi mereka. Ini dilakukan dengan tujuan menyederhanakan pengelolaan sejumlah besar data dan membangun tren mereka.

Setelah diatur di kelas -kelas ini untuk frekuensi mereka, data membentuk a Distribusi frekuensi, dari mana informasi utilitas diekstraksi melalui karakteristiknya.

Gambar 1. Dengan data yang dikelompokkan, Anda dapat membangun grafik dan menghitung parameter statistik yang menggambarkan tren. Sumber: Pixabay.

Selanjutnya kita akan melihat contoh sederhana dari data yang dikelompokkan:

Misalkan perawakan 100 siswa perempuan, yang dipilih dari antara semua kursus fisika dasar universitas, diukur dan hasil berikut diperoleh:

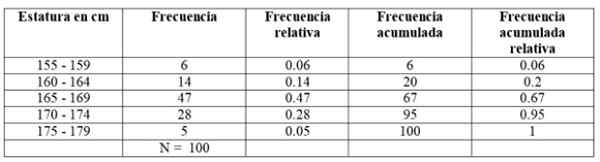
Hasil yang diperoleh dibagi menjadi 5 kelas, yang muncul di kolom kiri.

Kelas pertama, antara 155 dan 159 cm, memiliki 6 siswa, kelas kedua 160 - 164 cm memiliki 14 siswa, kelas ketiga dari 165 hingga 169 cm adalah satu dengan jumlah anggota terbesar: 47. Kemudian ikuti kelas 170-174 cm dengan 28 siswa dan akhirnya satu dari 175 hingga 179 cm dengan hanya 5.

Jumlah anggota dari setiap kelas justru frekuensi salah satu Frecuency absolut Dan dengan menambahkan semuanya, total data diperoleh, yang dalam contoh ini adalah 100.

[TOC]

Karakteristik distribusi frekuensi

Frekuensi

Seperti yang telah kita lihat, frekuensinya adalah berapa kali fakta diulangi. Dan untuk memfasilitasi perhitungan sifat distribusi, seperti rata -rata dan varian, jumlah berikut didefinisikan:

-Frekuensi akumulasi: Diperoleh dengan menambahkan frekuensi kelas dengan frekuensi akumulasi anterior. Yang pertama dari semua frekuensi bertepatan dengan interval yang dimaksud, dan yang terakhir adalah jumlah total data.

-Frekuensi relatif: Dihitung dengan membagi frekuensi absolut dari setiap kelas dengan jumlah total data. Dan jika berkembang biak dengan 100 Anda memiliki persentase persentase persentase.

Dapat melayani Anda: fungsi vektor

-Akumulasi frekuensi relatif: Ini adalah jumlah frekuensi relatif dari setiap kelas dengan akumulasi sebelumnya. Frekuensi relatif yang terakhir dari akumulasi harus sama dengan 1.

Sebagai contoh kami, frekuensinya seperti ini:

Batasan

Nilai ekstrem dari setiap kelas atau interval disebut Batas kelas. Seperti yang bisa kita lihat, setiap kelas memiliki batas bawah dan satu lebih besar. Sebagai contoh, kelas pertama dari penelitian tentang stature memiliki batas kurang dari 155 cm dan satu lebih besar dari 159 cm.

Contoh ini memiliki batas yang didefinisikan dengan jelas, namun mungkin.

Perbatasan

Tinggi adalah variabel kontinu, sehingga dapat dipertimbangkan bahwa kelas pertama sebenarnya dimulai pada 154.5 cm, karena dengan membulatkan nilai ini ke bilangan bulat terdekat, 155 cm diperoleh.

Kelas ini mencakup semua nilai hingga 159.5 cm, karena dari ini, staturnya dibulatkan menjadi 160.0 cm. Perawakan 159.7 cm sudah menjadi milik kelas berikutnya.

Batas kelas nyata dari contoh ini adalah, dalam CM:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplitudo

Luasnya kelas diperoleh dengan mengurangi perbatasan. Untuk interval pertama dari contoh kami, Anda memiliki 159.5 - 154.5 cm = 5 cm.

Pembaca dapat memverifikasi bahwa untuk interval lain dari contoh amplitudo juga hasil dari 5 cm. Namun, patut dicatat bahwa distribusi dapat dibangun dengan interval amplitudo yang berbeda.

Itu dapat melayani Anda: aturan t: karakteristik, sehingga itu, contoh

Merek kelas

Ini adalah titik medium interval dan diperoleh dengan rata -rata antara batas atas dan batas bawah.

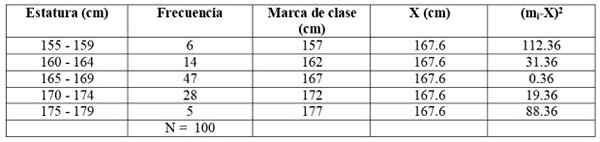
Sebagai contoh kami, merek kelas satu adalah (155 + 159)/2 = 157 cm. Pembaca dapat memverifikasi bahwa merek kelas yang tersisa adalah: 162, 167, 172 dan 177 cm.

Menentukan merek kelas adalah penting, karena diperlukan untuk menemukan rata -rata aritmatika dan varian distribusi.

Ukuran kecenderungan pusat dan dispersi untuk data yang dikelompokkan

Tindakan kecenderungan sentral yang paling banyak digunakan adalah rata -rata, median dan mode, dan menggambarkan secara tepat kecenderungan data yang akan dikelompokkan di sekitar nilai pusat tertentu.

Setengah

Ini adalah salah satu langkah kecenderungan utama utama. Dalam data yang dikelompokkan, rata -rata aritmatika dapat dihitung menggunakan rumus:

 Di mana:

-X adalah rata -rata

-F_yo adalah frekuensi kelas

-M_yo Itu adalah merek kelas

-G adalah jumlah kelas

-n adalah jumlah total data

Median

Untuk median Anda harus mengidentifikasi interval di mana pengamatan N/2 berada. Dalam contoh kami pengamatan ini adalah nomor 50, karena ada total 100 data. Pengamatan ini dalam interval 165-169 cm.

Maka Anda harus interpolasi untuk menemukan nilai numerik yang sesuai dengan pengamatan itu, yang rumusnya digunakan:

Di mana:

-C = lebar interval di mana median berada

-B_M = Perbatasan bawah interval tempat median berada

-F_M = Jumlah pengamatan yang terkandung dalam interval median

-N/2 = setengah dari total data

-F_Bm = Jumlah total pengamatan sebelum interval median

Mode

Untuk fashion, kelas modal diidentifikasi, yang berisi sebagian besar pengamatan, yang merek kelasnya dikenal.

Dapat melayani Anda: piramida heksagonal

Varians dan standar deviasi

Varians dan standar deviasi adalah ukuran dispersi. Jika kami menunjukkan varian dengan S² Dan untuk standar deviasi, yang merupakan akar kuadrat dari varian sebagai s, untuk data yang dikelompokkan kita akan memiliki masing -masing:

DAN

Olahraga diselesaikan

Untuk distribusi perawakan mahasiswa yang diusulkan di awal, hitung nilai -nilai:

a) rata -rata

b) Medium

c) mode

d) Varians dan standar deviasi.

Gambar 2. Ketika datang ke banyak nilai, seperti status sekelompok besar siswa, lebih baik mengelompokkan data di kelas. Sumber: Pixabay.

Solusi untuk

Mari kita bangun tabel berikut untuk memfasilitasi perhitungan:

Melalui ekspresi untuk kelompok rata -rata yang dikelompokkan di atas:

Mengganti nilai dan melaksanakan jumlah secara langsung:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Solusi b

Interval yang dimiliki median adalah 165-169 cm karena itu adalah interval yang paling sering.

Mari kita identifikasi masing -masing nilai ini dalam contoh, dengan bantuan Tabel 2:

C = 5 cm (lihat bagian amplitudo)

B_M = 164.5 cm

F_M = 47

N/2 = 100/2 = 50

F_Bm = 20

Mengganti dalam formula:

Solusi c

Interval yang terkandung dalam sebagian besar pengamatan adalah 165-169 cm, yang merek kelasnya 167 cm.

Solusi d

Kami memperluas tabel sebelumnya dengan menambahkan dua kolom tambahan:

Kami menerapkan formula:

Dan kami mengembangkan jumlahnya:

S² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Karena itu:

S = √21.35 cm² = 4.6 cm

Referensi

1. Berenson, m. 1985. Statistik untuk Administrasi dan Ekonomi. Inter -American s.KE.
2. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
3. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
4. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
5. Spiegel, m. 2009. Statistik. Seri Schaum. 4 ta. Edisi. Bukit McGraw.
6. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.