Guncangan elastis dalam dimensi, kasus khusus, latihan

Itu guncangan elastis o Tabrakan elastis terdiri dari interaksi singkat tetapi intens antara objek, di mana jumlah gerakan dan energi kinetik dipertahankan. Choques adalah peristiwa yang sangat sering di alam: dari partikel subatomik hingga galaksi, melewati bola biliar dan mobil kejut di taman atraksi, semuanya adalah objek yang mampu bertabrakan.

Selama tabrakan atau guncangan, kekuatan interaksi antara objek sangat intens, jauh lebih banyak daripada yang dapat bertindak secara eksternal. Dengan cara ini dapat ditegaskan bahwa selama tabrakan, partikel membentuk sistem yang terisolasi.

Tabrakan antara bola biliar dapat dianggap elastis. Sumber: Pixabay.

Dalam hal ini terpenuhi bahwa:

Di mana P Itu adalah jumlah vektor gerakan, yang besarnya MV (Massa kecepatan). Jika turunannya P adalah nol, artinya itu P itu konstan. Dan ini berarti tidak berbeda, bahwa itu dilestarikan. Karena itu kami dapat menegaskan itu:

P_{salah satu} = P_F

Jumlah Gerakan P_{salah satu} Sebelum tabrakan sama dengan setelah tabrakan. Ini dipenuhi untuk tabrakan jenis apa pun, baik elastis maupun tidak elastis.

Sekarang Anda harus mempertimbangkan hal berikut: Selama tabrakan, objek mengalami deformasi tertentu. Saat bentrokannya elastis, objek dengan cepat mendapatkan kembali bentuk aslinya.

[TOC]

Konservasi energi kinetik

Biasanya selama kejutan, bagian dari energi objek dihabiskan dalam panas, deformasi, suara dan kadang -kadang bahkan dalam menghasilkan cahaya. Jadi energi kinetik sistem setelah tabrakan kurang dari energi kinetik asli.

Saat Kinetic Energy K, itu dipertahankan kemudian:

K_{salah satu} = K_F

Yang berarti bahwa kekuatan yang bertindak selama tabrakan konservatif. Sementara tabrakan berlangsung, energi kinetik diubah secara singkat menjadi energi potensial dan kemudian merupakan energi kinetik lagi. Energi kinetik masing -masing bervariasi, tetapi jumlahnya tetap konstan.

Tabrakan elastis sempurna tidak sering terjadi, meskipun bola biliar adalah pendekatan yang cukup baik, serta tabrakan yang terjadi antara molekul Gase yang ideal.

Guncangan elastis dalam dimensi

Mari kita periksa tabrakan dua partikel ini dalam satu dimensi; Yaitu partikel yang berinteraksi bergerak, katakanlah, di sepanjang sumbu x. Misalkan mereka memiliki massa M₁ Dan M₂. Kecepatan awal masing -masing atau₁ Dan atau₂ masing -masing. Kecepatan terakhirnya v₁ Dan v₂.

Kita dapat melakukannya tanpa notasi vektor, karena gerakan dilakukan di sepanjang sumbu x, namun, tanda-tanda (-) dan (+) menunjukkan makna gerakan tersebut. Di sebelah kiri adalah negatif dan ke kanan positif, dengan konvensi.

Dapat melayani Anda: Jaringan Bravais: Konsep, Karakteristik, Contoh, Latihan

-Rumus untuk tabrakan elastis

Untuk jumlah gerakan

M₁atau₁ + M₂atau₂ = m₁v₁ + M₂v₂

Untuk energi kinetik

½ m₁atau²₁ + ½ m₂atau²₂ = ½ m₁v²₁ +  ½ m₂v²₂

Setiap kali massa dan kecepatan awal diketahui, dimungkinkan untuk menyusun kembali persamaan untuk menemukan kecepatan akhir.

Masalahnya adalah bahwa pada prinsipnya, itu perlu. Ideal adalah menemukan ekspresi yang tidak mengandungnya.

Yang pertama adalah melakukan tanpa faktor ½ dan mengatur ulang kedua persamaan sedemikian rupa sehingga tanda negatif muncul dan massa dapat menjadi faktor:

M₁atau₁ - M₁v₁ = M₂v₂ - M₂atau₂

M₁atau²₁ - M₁v²₁  = +M₂v²₂ - M₂atau²₂

Diungkapkan dengan cara ini:

M₁(atau₁ - v₁ ) = m₂(v₂ - atau₂)

M₁(atau²₁ - v²₁ ) = m₂ (v²₂ - atau²₂)

Penyederhanaan untuk menghilangkan kotak dari kecepatan

Sekarang Anda harus menggunakan produk terkenal, itu menambah perbedaan dalam persamaan kedua, yang memperoleh ekspresi yang tidak mengandung kotak, seperti yang diinginkan:

M₁(atau₁ - v₁ ) = m₂(v₂ - atau₂)

M₁(atau₁ - v₁ ) (atau₁ + v₁ ) = m₂ (v₂ - atau₂) (v₂ + atau₂)

Langkah selanjutnya adalah mengganti persamaan pertama di yang kedua:

M₂(v₂ - atau₂) (atau₁ + v₁ ) = m₂ (v₂ - atau₂) (v₂ + atau₂)

Dan saat istilah itu diulangi M₂(v₂ - atau₂) Di kedua sisi kesetaraan, istilah ini dibatalkan dan seperti ini:

(atau₁ + v₁) = (V₂ + atau₂)

Atau bahkan lebih baik:

atau₁ - atau₂= v₂ -  v₁

Kecepatan akhir v₁ dan v₂ dari partikel

Sekarang ada dua persamaan linier yang lebih mudah bekerja. Kami akan menempatkannya lagi di bawah yang lain:

M₁atau₁ + M₂atau₂ = m₁v₁ + M₂v₂

atau₁ - atau₂= v₂ -  v₁

Mengalikan persamaan kedua dengan M₁ Dan menambahkan istilah ke jangka waktu tetap:

M₁atau₁ + M₂atau₂ = m₁v₁ + M₂v₂

M₁atau₁ - M₁atau₂= m₁v₂ - M₁ v₁

-

2 m₁atau₁ + (M₂ - M₁) atau₂ = (m₂ + M₁) v₂

Dan sudah mungkin untuk membersihkan v₂. Misalnya:

Perawatan serupa dapat dilakukan untuk menemukan persamaan v₁. Pembaca dibiarkan sebagai latihan untuk menunjukkan itu:

Kasus khusus dalam tabrakan elastis

Sekarang persamaan tersedia untuk kecepatan akhir dari kedua partikel, sekarang saatnya untuk menganalisis beberapa situasi khusus.

Dua massa identik

Kemudian M₁ = m₂ = m Dan:

v₁ = u₂

v₂ = u₁

Partikel hanya menukar kecepatan mereka setelah tabrakan.

Dua massa identik, salah satunya awalnya sedang istirahat

Lagi  M₁ = m₂ = m dan dengan asumsi itu atau₁ = 0:

v₁ = u₂

v₂ = 0

Setelah kecelakaan, partikel yang sedang istirahat memperoleh kecepatan partikel yang sama yang telah bergerak, dan pada gilirannya berhenti.

Dapat melayani Anda: tekanan hidrolik

Dua massa yang berbeda, salah satunya awalnya sedang istirahat

Dalam hal ini, misalkan atau₁ = 0, Tapi massa berbeda:

Bagaimana jika M₁ jauh lebih besar dari M₂?

Itu terjadi m₁ Tetap diam dan M₂ Itu dikembalikan dengan kecepatan yang sama dengan yang berdampak.

Koefisien atau aturan restitusi Huygens-Newton

Sebelumnya hubungan berikut antara kecepatan untuk dua objek dalam tabrakan elastis disimpulkan: atau₁ - atau₂ = v₂ -  v₁. Perbedaan -perbedaan ini adalah kecepatan relatif sebelum dan sesudah tabrakan. Secara umum, untuk tabrakan terpenuhi bahwa:

atau₁ - atau₂ = -(v₁ -  v₂)

Konsep kecepatan relatif lebih dihargai jika pembaca membayangkan bahwa itu ada pada salah satu partikel dan dari posisi ini mengamati kecepatan partikel lainnya bergerak. Persamaan sebelumnya ditulis ulang seperti ini:

Jika energi kinetik tidak dipertahankan, maka hasil bagi yang ditunjukkan akan kurang dari 1. Mari kita menelepon Dan dengan nilai hasil bagi tanpa dimensi tersebut:

O Nah:

Nilai dari Dan adalah antara 0 dan 1 dan dipanggil koefisien restitusi. Saat bentrokan elastis, e = 1. Ketika benar -benar tidak elastis, e = 0, sedangkan jika memiliki nilai menengah lainnya, beberapa energi kinetik telah tersebar dalam jenis energi lainnya.

Latihan terpecahkan

-Latihan diselesaikan 1

Bola biliar bergerak ke kiri pada 30 cm/s, bertabrakan dari depan dengan bola identik lain yang bergerak ke kanan hingga 20 cm/s. Kedua bola memiliki adonan yang sama dan kecelakaannya sangat elastis. Temukan kecepatan setiap bola setelah dampak.

Larutan

atau₁ = -30 cm/s

atau₂ = +20 cm/s

Ini adalah kasus khusus bahwa dua massa identik bertabrakan dalam dimensi elastis, oleh karena itu kecepatan dipertukarkan.

v₁ = +20 cm/s

v₂ = -30 cm/s

-Latihan diselesaikan 2

Koefisien restitusi bola yang memantul di tanah sama dengan 0,82. Jika Anda jatuh dari istirahat, sebagian kecil dari ketinggian asli Anda akan mencapai bola setelah memantul sekali? Dan setelah 3 rebound?

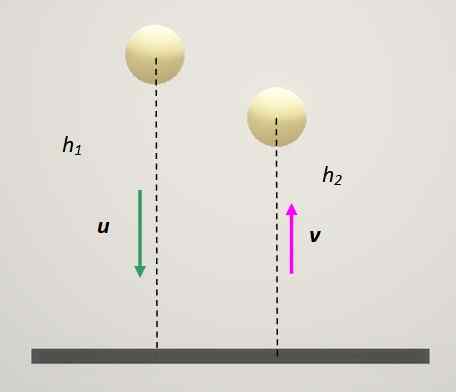Sebuah bola memantul di permukaan yang kuat dan kehilangan ketinggian dengan setiap rebound. Sumber: Made sendiri.

Larutan

Tanah bisa objek 1 dalam persamaan koefisien restitusi. Dan selalu beristirahat, sehingga:

Arah negatif dipilih dan positif. Kecepatan objek yang dilepaskan secara bebas dari ketinggian tertentu H_{salah satu} adalah:

Tanda (-) menunjukkan bahwa bola turun:

Ini dapat melayani Anda: Torricelli Eksperimen: Tindakan Tekanan Atmosfer, Pentingnya

 

Dengan kecepatan ini memantul:

 

Tanda + menunjukkan bahwa itu adalah kecepatan naik. Dan menurutnya, bola mencapai ketinggian maksimum:

 

Sekarang dia kembali ke tanah lagi dengan kecepatan yang sama, tetapi tanda yang berlawanan:

Dan memantul dengan:

Ini mencapai ketinggian maksimum:

Mencapai tanah lagi dengan:

Rebound berturut -turut

Setiap kali bola memantul dan naik, Anda harus melipatgandakan kecepatan lagi dengan 0.82:

Dan mencapai ketinggian maksimum yang ditentukan oleh kuadrat kecepatan tersebut:

Pada titik ini h₃ sekitar 30% dari H_{salah satu}. Apa yang akan menjadi ketinggian di rebound ke -6 tanpa harus membuat perhitungan sedetail yang sebelumnya?

saya akan H₆ = 0.82¹² H_{salah satu} = 0.092H_{salah satu} atau hanya 9% dari H_{salah satu}.

-Latihan diselesaikan 3

Blok 300 g bergerak ke utara ke 50 cm/s dan bentrokan terhadap blok 200 g yang diarahkan ke selatan 100 cm/s. Asumsikan bahwa bentrokan itu sangat elastis. Temukan Kecepatan Setelah Dampak.

Data

M₁ = 300 g; atau₁ = + 50 cm/s

M₂ = 200 g; atau₂ = -100 cm/s

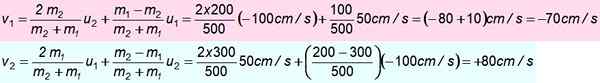
-Latihan diselesaikan 4

Massa m dilepaskan₁ = 4 kg dari titik yang ditunjukkan di trek tanpa gesekan, sampai bertabrakan dengan m₂ = 10 kg saat istirahat. Untuk betapa tinggi m adalah m₁ Setelah tabrakan?

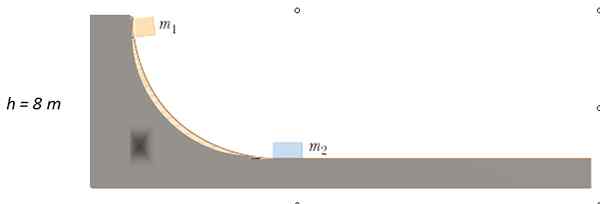
Larutan

Karena tidak ada gesekan, energi mekanik dipertahankan untuk menemukan kecepatan atau₁ dengan apa M₁ dampak  M_2. Awalnya energi kinetik adalah 0, karena M₁ bagian dari sisanya. Saat bergerak di permukaan horizontal, ia tidak memiliki tinggi, jadi energi potensial adalah 0.

MGH = ½ MU₁ ²

 

atau₂ = 0

Sekarang kecepatan M₁ Setelah tabrakan:

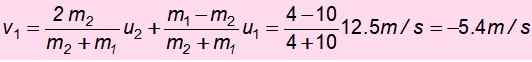
Tanda negatif berarti telah dikembalikan. Dengan kecepatan ini naik dan energi mekanik dipertahankan lagi untuk menemukan H ', Tinggi di mana ia berhasil naik setelah kecelakaan:

½ mV₁² = mgh '

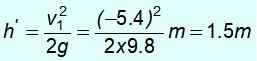
Perhatikan bahwa Anda tidak kembali ke titik awal pada ketinggian 8 m. Itu tidak memiliki energi yang cukup karena memberikan sebagian energi kinetik massa M_1.

Referensi

1. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Dasar -dasar fisika. Pearson. 135-155.
3. Serway, r., Vulle, c. 2011. Dasar -dasar fisika. 9^na Pembelajaran Cengage. 172 -182
4. Tipler, hlm. (2006) Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 1. Editorial dikembalikan. 217-238
5. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit MacGraw. 185 -195