Rumus koefisien korelasi, perhitungan, interpretasi, contoh

Dia Koefisien Korelasi Dalam statistik ini merupakan indikator yang mengukur tren dua variabel kuantitatif x dan y untuk memiliki hubungan linieritas atau proporsionalitas di antara mereka.

Secara umum, pasangan variabel x dan y adalah dua karakteristik dari populasi yang sama. Misalnya, x bisa menjadi ketinggian seseorang dan beratnya.

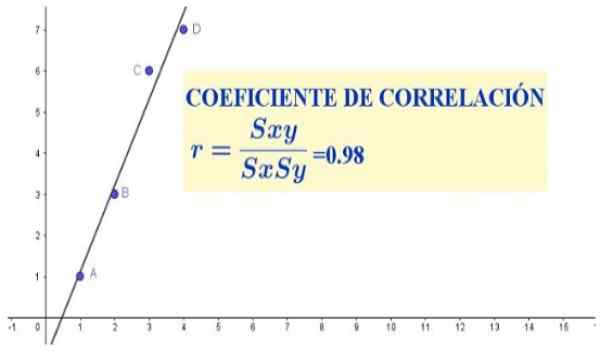
Gambar 1. Koefisien korelasi untuk empat pasangan data (x, y). Sumber: f. Zapata.

Dalam hal ini, koefisien korelasi akan menunjukkan apakah ada rasio proporsionalitas antara tinggi dan berat dari populasi tertentu.

Koefisien korelasi linier Pearson dilambangkan dengan surat itu R huruf kecil dan nilai minimum dan maksimumnya adalah -1 dan +1 masing -masing. 

Nilai r = +1 akan menunjukkan bahwa seluruh pasangan (x, y) benar -benar selaras dan bahwa ketika x tumbuh, dan akan tumbuh dalam proporsi yang sama. Di sisi lain, jika itu terjadi bahwa r = -1, himpunan pasangan juga akan diselaraskan dengan sempurna, tetapi dalam hal ini ketika X tumbuh, dan berkurang dalam proporsi yang sama.

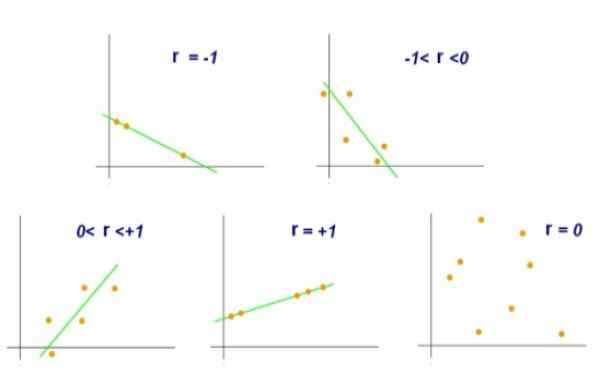Gambar 2. Nilai yang berbeda dari koefisien korelasi linier. Sumber: Wikimedia Commons.

Di sisi lain, nilai r = 0 akan menunjukkan bahwa tidak ada korelasi linier antara variabel x dan y. Sementara nilai r = +0.8 akan menunjukkan bahwa pasangan (x, y) cenderung mengelompokkan ke satu sisi dan satu sisi dari garis tertentu.

Rumus untuk menghitung koefisien korelasi R adalah sebagai berikut:

Di mana pembilang mewakili kovarians antara variabel x dan y, sedangkan denominator adalah produk dari standar deviasi untuk variabel x dan standar deviasi untuk variabel dan.

Cara menghitung koefisien korelasi?

Koefisien korelasi linier adalah jumlah statistik yang dimasukkan ke dalam kalkulator ilmiah, di sebagian besar spreadsheet dan program statistik.

Dapat melayani Anda: paraboloid hiperbolik: definisi, sifat, dan contoh

Namun, lebih mudah untuk mengetahui bagaimana rumus yang mendefinisikannya diterapkan, dan untuk ini perhitungan terperinci akan ditampilkan, dilakukan pada set data kecil.

Dan seperti yang dinyatakan pada bagian sebelumnya, koefisien korelasi adalah kovarians SXY dibagi dengan produk standar deviasi SX untuk variabel x dan sy untuk variabel dan.

Kovarians dan varian

Kovarians SXY adalah:

Sxy = [σ (xi -) (yi -)] / (n -1)

Dimana jumlahnya dari 1 ke pasangan n (xi, yi). E adalah stoking aritmatika dari data masing -masing.

Untuk bagiannya, standar deviasi untuk variabel x adalah akar kuadrat dari varian set data XI, dengan I dari 1 ke n:

Sx = √ [σ (xi -)^2) / (n -1)]

Demikian pula, standar deviasi untuk variabel dan merupakan akar kuadrat dari varian set data YI, dengan I dari 1 ke n:

Sy = √ [σ (yi -)² ) / (N-1)]

Kasus ilustrasi

Untuk menunjukkan secara rinci cara untuk menghitung koefisien korelasi, kami akan mengambil set empat pasang data berikut 

(X, y): (1, 1); (23); (3, 6) dan (4, 7).

Pertama kita menghitung rata -rata aritmatika untuk x dan y, sebagai berikut:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Maka parameter yang tersisa dihitung:

Kovarians SXY

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Dapat melayani Anda: aturan derivasi (dengan contoh)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Deviasi Standar SX

Sx = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Sy Deviasi Standar

Sx = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Koefisien pagar r

R = 3.5 / (1.29 * 2.75) = 0.98

Penafsiran

Dalam kumpulan data dari kasus sebelumnya ada korelasi linier yang kuat antara variabel x dan y, yang memanifestasikan baik dalam grafik dispersi (yang dapat dilihat pada Gambar 1) dan dalam koefisien korelasi, yang melemparkan nilai yang cukup dekat dengan unit.

Sejauh koefisien korelasi lebih dekat ke 1 atau -1, lebih masuk akal membuat pengaturan data ke suatu garis, hasil dari regresi linier.

Regresi linier

Garis regresi linier diperoleh dari Metode kuadrat terkecil. di mana parameter garis regresi diperoleh dari minimalisasi jumlah kuadrat perbedaan antara nilai dan estimasi dan YI data N.

Di sisi lain, parameter A dan B dari garis regresi y = a + bx, diperoleh dengan metode kotak minimum, adalah: adalah: adalah: adalah: adalah: adalah: adalah:

*B = sxy / (sx²) Untuk lereng

*A = - b untuk persimpangan garis regresi dengan sumbu dan.

Ingatlah bahwa SXY adalah kovarians yang didefinisikan di atas dan SX² Itu adalah varian atau kuadrat dari standar deviasi yang ditentukan sebelumnya. E adalah sarana aritmatika dari data X dan dan masing -masing.

Contoh

Koefisien korelasi digunakan untuk menentukan apakah ada korelasi tipe linier antara dua variabel. Ini berlaku ketika variabel yang akan dipelajari adalah kuantitatif dan juga, mereka seharusnya mengikuti distribusi tipe normal.

Dapat melayani Anda: aturan korespondensi suatu fungsi

Contoh ilustratif yang kami miliki di bawah ini: ukuran tingkat obesitas adalah indeks massa tubuh, yang diperoleh dengan membagi berat satu orang menjadi kilogram antara ketinggian yang sama di unit kuadrat ke kuadrat.

Diinginkan untuk mengetahui apakah ada korelasi yang kuat antara indeks massa tubuh dan konsentrasi kolesterol HDL dalam darah, diukur dalam milimol per liter. Untuk tujuan ini, sebuah penelitian telah dilakukan dengan 533 orang yang dirangkum dalam grafik berikut, di mana setiap titik mewakili data seseorang.

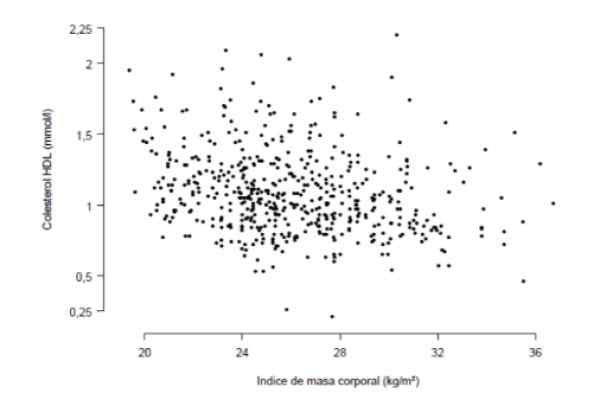Gambar 3. Studi IMC dan kolesterol HDL pada 533 pasien. Sumber: Institut Ilmu Kesehatan Aragon (IAC).

Dari pengamatan grafik yang cermat, maka ada tren linier (tidak terlalu ditandai) tertentu antara konsentrasi kolesterol HDL dan indeks massa tubuh. Ukuran kuantitatif dari tren ini adalah koefisien korelasi yang untuk kasus ini ternyata r = -0.276.

Referensi

1. González c. Statistik umum. Pulih dari: tarwi.La Molina.Edu.pe
2. IACS. Institut Ilmu Kesehatan Aragon. Diperoleh dari: ICS-Aragon.com 
3. Salazar c. dan Castillo s. Prinsip Statistik Dasar. (2018). Diperoleh dari: dspace.Uce.Edu.Ec
4. Superprof. Koefisien Korelasi. Pulih dari: superprof.adalah
5. USAC. Manual Statistik Deskriptif. (2011). Pulih dari: statistik.rekayasa.USAC.Edu.GT
6. Wikipedia. Koefisien Korelasi Pearson. Pulih dari: is.Wikipedia.com.