Rumus distribusi Poisson, persamaan, model, properti

Itu distribusi racun Ini adalah distribusi probabilitas diskrit, di mana Anda dapat mengetahui probabilitas bahwa, dalam sampel besar dan selama interval tertentu, suatu peristiwa yang probabilitasnya kecil terjadi.

Seringkali, distribusi Poisson dapat digunakan sebagai pengganti distribusi binomial, selama kondisi berikut yang dijelaskan dipenuhi: sampel besar dan probabilitas kecil.

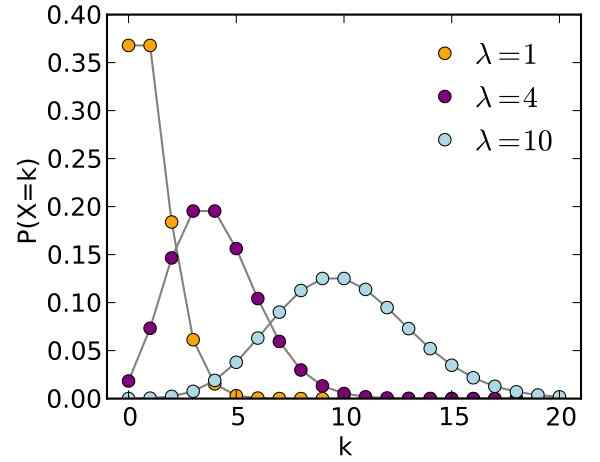
Gambar 1. Grafik distribusi Poisson untuk parameter yang berbeda. Sumber: Wikimedia Commons.

Siméon-Denis Poisson (1781-1840) membuat distribusi ini yang menyandang namanya, sangat berguna dalam hal peristiwa yang tidak terduga. Poisson menerbitkan hasilnya pada tahun 1837, sebuah pekerjaan penelitian tentang probabilitas terjadinya hukuman kriminal yang salah.

Selanjutnya, para peneliti lain mengadaptasi distribusi di daerah lain, misalnya, jumlah bintang yang bisa dalam volume ruang tertentu, atau probabilitas bahwa seorang prajurit akan mati karena keluh kuda.

[TOC]

Formula dan Persamaan

Bentuk matematika distribusi Poisson adalah sebagai berikut:

 - Variabel acaknya Dan

- μ (juga kadang -kadang dilambangkan sebagai λ) Itu adalah parameter rata -rata atau distribusi

- Nomor Euler: E = 2.71828

- Probabilitas mendapatkan y = k adalah p

- k Ini adalah jumlah keberhasilan 0, 1,2,3 ..

- N Ini adalah jumlah tes atau peristiwa (ukuran sampel)

Variabel acak diskrit, sesuai namanya, bergantung pada peluang dan hanya mengambil nilai diskrit: 0, 1, 2, 3, 4 ..., k.

Rata -rata distribusi diberikan oleh:

Varian σ, yang mengukur dispersi data, adalah parameter penting lainnya. Untuk distribusi Poisson itu adalah:

σ = μ

Poisson menetapkan bahwa ketika n → ∞, dan p → 0, rata -rata μ -jama disebut nilai yang diharapkan- Itu cenderung konstan:

μ → Konstan

Penting: P Ini adalah probabilitas terjadinya peristiwa dengan mempertimbangkan total populasi, sementara P (y) Itu adalah prediksi Poisson tentang sampel.

Model dan Properti

Distribusi Poisson memiliki sifat -sifat berikut:

-Ukuran sampel besar: N → ∞.

-Peristiwa atau peristiwa yang dipertimbangkan tidak tergantung satu sama lain dan terjadi secara acak.

-Kemungkinan P Acara apa tertentu Dan Itu terjadi untuk periode waktu tertentu sangat kecil: P → 0.

-Probabilitas lebih dari satu peristiwa dalam interval waktu adalah 0.

-Nilai rata -rata mendekati konstan yang diberikan oleh: μ = n.P (n adalah ukuran sampel)

-Karena dispersi σ sama dengan μ, karena mengadopsi nilai yang lebih besar, variabilitas juga lebih besar.

-Peristiwa harus didistribusikan secara merata dalam interval waktu yang digunakan.

-Himpunan nilai acara yang mungkin terjadi Dan Ini adalah: 0,1,2,3,4 .. .

Dapat melayani Anda: Eksperimen acak: konsep, ruang sampel, contoh

-Jumlah dari yo Variabel yang mengikuti distribusi Poisson, juga merupakan variabel Poisson lainnya. Nilai rata -rata adalah jumlah nilai rata -rata dari variabel -variabel ini.

Perbedaan dengan distribusi binomial

Distribusi Poisson berbeda dari distribusi binomial dalam aspek -aspek penting berikut:

-Distribusi binomial dipengaruhi baik oleh ukuran sampel S dan dengan probabilitas P, Tapi distribusi Poisson hanya dipengaruhi oleh rata -rata μ.

-Dalam distribusi binomial, nilai yang mungkin dari variabel acak Dan Mereka 0,1,2, ..., sebaliknya dalam distribusi Poisson tidak ada batas atas untuk nilai -nilai ini.

Contoh

Poisson awalnya menerapkan distribusinya yang terkenal untuk kasus -kasus hukum, tetapi di tingkat industri, salah satu kegunaannya yang pertama adalah dalam pembuatan bir. Dalam proses ini tanaman ragi digunakan untuk fermentasi.

Ragi terdiri dari sel hidup, yang populasinya bervariasi dalam waktu. Dalam pembuatan bir, perlu untuk menambahkan jumlah yang diperlukan, jadi perlu untuk mengetahui jumlah sel per satuan volume.

Selama Perang Dunia II, distribusi Poisson digunakan untuk mengetahui apakah Jerman benar -benar menunjuk ke London dari Calais, atau hanya menembak secara acak. Ini penting bagi Sekutu untuk menentukan seberapa baik teknologi yang tersedia untuk Nazi.

Aplikasi praktis

Aplikasi distribusi Poisson selalu merujuk pada jumlah waktu atau jumlah ruang. Dan karena probabilitas kejadiannya kecil, ia juga dikenal sebagai "hukum peristiwa langka".

Berikut adalah daftar acara yang termasuk dalam salah satu kategori ini:

-Pendaftaran partikel dalam peluruhan radioaktif, yang seperti pertumbuhan sel ragi, adalah fungsi eksponensial.

-Jumlah kunjungan ke situs web tertentu.

-Kedatangan orang untuk berbaris untuk membayar atau dihadiri (teori ekor).

-Jumlah mobil yang melewati titik tertentu di jalan, untuk interval waktu tertentu.

Gambar 2. Jumlah mobil yang melewati suatu titik mengikuti sekitar distribusi Poisson. Sumber: Pixabay.

-Mutasi menderita dalam rantai DNA tertentu setelah menerima paparan radiasi.

-Nomor meteor diameter lebih besar dari 1 m jatuh dalam setahun.

-Cacat per meter persegi kain.

-Jumlah sel darah dalam 1 sentimeter kubik.

-Panggilan per menit ke pertukaran telepon.

-Percikan cokelat hadir dalam 1 kg adonan kue.

-Jumlah pohon yang terinfeksi di 1 hektar hutan.

Perhatikan bahwa variabel acak ini mewakili berapa kali peristiwa terjadi untuk periode waktu yang tetap (Panggilan per menit ke pertukaran telepon), atau wilayah ruang tertentu (Cacat kain per meter persegi).

Dapat melayani Anda: variasi proporsional

Peristiwa ini, seperti yang sudah ditetapkan, tidak tergantung pada waktu yang telah berlalu sejak kejadian terakhir.

Mendekati distribusi binomial dengan distribusi Poisson

Distribusi Poisson adalah pendekatan yang baik untuk distribusi binomial selama:

-Ukuran sampel besar: n ≥ 100

-Kemungkinan P IS kecil: p ≤ 0,1

- μ berada di urutan: NP ≤ 10

Dalam kasus seperti itu, distribusi Poisson adalah alat yang sangat baik, karena distribusi binomial dapat menjadi rumit untuk diterapkan dalam kasus ini.

Latihan terpecahkan

Latihan 1

Sebuah studi seismologis menentukan bahwa selama 100 tahun terakhir, ada 93 gempa bumi besar di seluruh dunia, setidaknya 6.0 pada skala richter -logarithmic-. Misalkan distribusi Poisson adalah model yang memadai dalam kasus ini. Menemukan:

a) Rata -rata terjadinya gempa bumi besar per tahun.

b) Ya P (y) Itu adalah kemungkinan terjadi Dan Gempa bumi untuk tahun yang dipilih secara acak, temukan probabilitas berikut:

P(0), P(1), P (2), P (3), P (4), P (5), P (6) dan P (7).

c) Hasil sebenarnya dari penelitian ini adalah sebagai berikut:

- 47 tahun (0 gempa bumi)

- 31 tahun (1 gempa bumi)

- 13 tahun (2 gempa bumi)

- 5 tahun (3 gempa bumi)

- 2 tahun (4 gempa bumi)

-  0 tahun (5 gempa bumi)

- 1 tahun (6 gempa bumi)

- 1 tahun (7 gempa bumi)

Bagaimana hasil ini dengan yang diperoleh dalam ayat b? Apakah distribusi Poisson adalah pilihan yang baik untuk memodelkan acara ini?

Solusi untuk)

a) Gempa bumi adalah peristiwa yang probabilitasnya P Dia kecil dan kami sedang mempertimbangkan periode waktu yang terbatas, dari satu tahun. Gempa rata -rata adalah:

μ = 93 /100 gempa bumi / tahun = 0.93 gempa bumi per tahun.

Solusi b)

b) Untuk menghitung probabilitas yang diminta, nilai diganti dalam formula yang diberikan di awal:

Misalnya untuk menemukan P (2), yang akan menjadi probabilitas bahwa akan ada 2 gempa bumi besar setahun:

y = 2

μ = 0.93

E = 2.71828

Dan inilah probabilitas bahwa ada 7 gempa bumi besar selama setahun:

Ini cukup kurang dari P (2).

Hasilnya tercantum di bawah ini:

P (0) = 0.395, p (1) = 0.367, p (2) = 0.171, p (3) = 0.0529, p (4) = 0.0123, p (5) = 0.00229, p (6) = 0.000355, p (7) = 0.0000471.

Misalnya, kita bisa mengatakan bahwa ada kemungkinan 39.5 % bahwa tidak ada gempa besar yang terjadi pada tahun tertentu. Atau bahwa ada 5,29 % bahwa 3 gempa bumi besar terjadi pada tahun itu.

Solusi C)

c) frekuensi dianalisis, dikalikan dengan n = 100 tahun:

39.5; 36.7; 17.1; 5.29; 1.23; 0.229; 0.0355 dan 0.00471.

Dapat melayani Anda: turunan aljabar

Misalnya:

- Frekuensi 39.5 menunjukkan bahwa, dalam 39.5 dari 100 tahun atau gempa bumi besar terjadi, kita dapat mengatakan bahwa itu cukup dekat dengan hasil yang benar -benar 47 tahun tanpa gempa bumi yang bagus.

Mari kita bandingkan hasil Poisson lain dengan hasil nyata:

- Nilai yang diperoleh dari 36.7 berarti bahwa dalam periode 37 tahun ada 1 gempa bumi besar. Hasil sebenarnya adalah bahwa dalam 31 tahun ada 1 gempa bumi besar, kebetulan dengan model.

- 17 diharapkan.1 tahun dengan 2 gempa bumi besar dan diketahui bahwa dalam 13 tahun, yang merupakan nilai yang dekat, ada efek 2 gempa bumi besar.

Oleh karena itu model Poisson dapat diterima untuk kasus ini.

Latihan 2

Perusahaan memperkirakan bahwa jumlah komponen yang gagal sebelum menyelesaikan 100 jam operasi, mengikuti distribusi Poisson. Jika jumlah rata -rata kegagalan adalah 8 pada waktu itu, temukan probabilitas berikut:

a) Komponen itu gagal dalam 25 jam.

b) Kegagalan kurang dari dua komponen, dalam 50 jam.

c) bahwa setidaknya tiga komponen gagal dalam 125 jam.

Solusi untuk)

a) Diketahui bahwa kesalahan rata -rata dalam 100 jam adalah 8, oleh karena itu dalam 25 jam bagian keempat kegagalan diharapkan, yaitu 2 kegagalan. Ini akan menjadi parameter μ.

Probabilitas 1 komponen gagal diminta, variabel acak adalah "komponen yang gagal sebelum 25 jam" dan nilainya y = 1. Dengan mengganti fungsi probabilitas:

 b) Sekarang variabel acak adalah "komponen yang gagal sebelum 50 jam". Parameternya μ = 4, Karena nilai kegagalan yang diharapkan dalam 50 jam adalah 4.

Namun, pertanyaannya adalah probabilitas bahwa kurang dari dua komponen gagal dalam 50 jam, bukan bahwa tepatnya 2 komponen gagal dalam 50 jam, oleh karena itu kita harus menambahkan probabilitas bahwa:

-Tidak ada yang gagal

-Gagal hanya 1

P (kurang dari 2 komponen) = p (0) + p (1)

P (kurang dari 2 komponen) = 0.0183+0.0732 = 0.0915

c) bahwa setidaknya 3 komponen gagal dalam 125, itu berarti bahwa 3, 4, 5 atau lebih pada waktu itu dapat gagal.

Probabilitas yang terjadi setidaknya satu dari beberapa peristiwa sama dengan 1, kecuali probabilitas bahwa tidak ada peristiwa yang akan terjadi.

-Peristiwa yang dicari adalah gagal 3 atau lebih komponen dalam 125 jam

-Bahwa peristiwa itu tidak terjadi berarti kurang dari 3 komponen gagal, yang probabilitasnya adalah: P (0)+p (1)+p (2)

Parameter μ distribusi dalam kasus ini adalah:

 μ = 8 + 2 = 10 kegagalan dalam 125 jam.

P (jatuh 3 atau lebih komponen) = 1- p (0)- p (1)- p (2) =

= 1-0.0026786 = 0.9972

Referensi

1. Mathworks. distribusi racun. Pulih dari: is.Mathworks.com
2. Mendenhall, w. 1981. Statistik untuk Administrasi dan Ekonomi. 3. edisi. Grup Editorial Iberoamerica.
3. Stat Trek. Ajari diri Anda sendiri statistik. Distribusi racun. Pulih dari: stattrek.com,
4. Triola, m. 2012. Statistik dasar. 11. Ed. Pendidikan Pearson.
5. Wikipedia. Distribusi racun. Diperoleh dari: di.Wikipedia.org