Rumus koefisien penentuan, perhitungan, interpretasi, contoh

Dia Koefisien Penentuan Ini adalah angka antara 0 dan 1 yang mewakili fraksi titik (x, y) yang mengikuti garis penyesuaian dengan regresi set data dengan dua variabel.

Itu juga dikenal sebagai kebaikan penyesuaian dan dilambangkan dengan r². Untuk menghitungnya, hasil bagi diambil antara varian data ŷi yang diperkirakan oleh model regresi dan varian data YI yang sesuai dengan setiap XI data.

R² = Sŷ / sy

Gambar 1. Koefisien korelasi untuk empat pasangan data. Sumber: f. Zapata.

Jika 100% data berada pada garis fungsi regresi, maka koefisien penentuan akan menjadi 1.

Sebaliknya, jika untuk set data dan fungsi penyesuaian tertentu, koefisien R R² Ternyata sama dengan 0.5, maka dapat dikatakan bahwa penyesuaian memuaskan atau bagus di 50%. 

Demikian pula, ketika model regresi melempar nilai r² kurang dari 0.5, ini menunjukkan bahwa fungsi penyesuaian yang dipilih tidak beradaptasi dengan memuaskan dengan data, oleh karena itu diperlukan untuk mencari fungsi penyesuaian lain.

Dan kapan Kovarians atau Koefisien Korelasi Itu cenderung nol, maka variabel x dan y dari data tidak terkait, dan karenanya r² juga akan cenderung nol.

[TOC]

Cara menghitung koefisien penentuan?

Pada bagian sebelumnya dikatakan bahwa koefisien penentuan dihitung dengan menemukan hasil bagi antara varian:

-Diperkirakan oleh fungsi regresi variabel dan 

-Variabel yi yang sesuai dengan masing -masing variabel xi. 

Dalam bentuk matematika, tetap seperti ini:

R² = Sŷ / sy

Dari formula ini mengikuti r itu² mewakili proporsi varian yang dijelaskan oleh model regresi. Atau, R dapat dihitung² Melalui rumus berikut, benar -benar setara dengan yang sebelumnya:

R² = 1 - (sε / sy)

Di mana Sε mewakili varian limbah εi = ŷi - yi, sedangkan sy adalah varian dari set data dari data data. Untuk menentukan ŷi fungsi regresi diterapkan, yang berarti menegaskan bahwa ŷi = f (xi).

Itu dapat melayani Anda: fraksi setara dengan 3/5 (solusi dan penjelasan)

Varians dari set data YI, dengan I dari 1 ke N dihitung dengan cara ini:

Sy = [σ (yi -)² ) / (N-1)]

Dan kemudian lanjutkan dengan cara yang sama untuk Sŷ atau untuk Sε.

Kasus ilustrasi

Dengan cara menunjukkan detail cara perhitungan Koefisien Penentuan Kami akan mengambil set empat pasang data berikut: 

(X, y): (1, 1); (23); (3, 6) dan (4, 7).

Penyesuaian regresi linier diusulkan untuk set data ini yang diperoleh dengan metode minimum kuadrat:

f (x) = 2.1 x - 1 

Menerapkan fungsi penyesuaian ini, rekan -rekan diperoleh:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) dan (4, 7.4).

Kemudian kami menghitung rata -rata aritmatika untuk x dan y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Varians sy

Sy = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Varians Sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Koefisien penentuan r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Penafsiran

Koefisien penentuan untuk kasus ilustratif yang dipertimbangkan di segmen sebelumnya ternyata 0.98. Artinya, penyesuaian linier melalui fungsi:

 f (x) = 2.1x - 1

Ini 98% dapat diandalkan untuk menjelaskan data yang diperolehnya melalui metode minimum kuadrat. 

Selain koefisien penentuan, ada Koefisien Korelasi Linier atau juga dikenal sebagai koefisien Pearson. Koefisien ini, dilambangkan sebagai R, Itu dihitung oleh hubungan berikut:

R = SXY / (SX SY)

Di sini pembilang mewakili kovarians antara variabel x dan y, sedangkan penyebut adalah produk dari standar deviasi untuk variabel x dan standar deviasi untuk variabel dan.

Koefisien Pearson dapat mengambil nilai antara -1 dan +1. Ketika koefisien ini cenderung +1 ada korelasi linier langsung antara x dan y. Jika sebaliknya cenderung -1, ada korelasi linier tetapi ketika X tumbuh dan berkurang. Akhirnya, hampir 0 tidak ada korelasi antara kedua variabel.

Dapat melayani Anda: Data yang dikelompokkan: Contoh dan olahraga diselesaikan

Perlu dicatat bahwa koefisien penentuan bertepatan dengan kuadrat koefisien Pearson, hanya ketika yang pertama telah dihitung berdasarkan penyesuaian linier, tetapi kesetaraan ini tidak berlaku untuk penyesuaian non -linier lainnya.

Contoh

- Contoh 1

Sekelompok siswa sekolah menengah berniat menentukan hukum empiris untuk periode pendulum sebagai fungsi panjangnya. Untuk mencapai tujuan ini, mereka membuat serangkaian pengukuran di mana mereka mengukur waktu osilasi pendulum untuk panjang yang berbeda memperoleh nilai -nilai berikut:

Panjang (m)	Periode
0.1	0.6
0.4	1.31
0.7	1.78
1	1.93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

Itu diminta untuk membuat grafik dispersi data dan membuat penyesuaian linier dengan regresi. Selain itu, tunjukkan persamaan regresi dan koefisien penentuannya.

Larutan

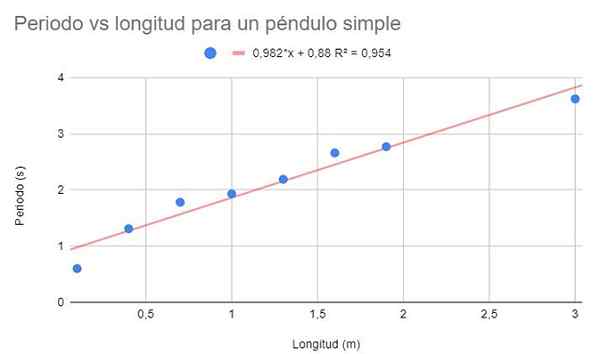Gambar 2. Solusi Grafis Latihan 1. Sumber: f. Zapata.

Koefisien penentuan yang cukup tinggi (95%) dapat diamati, sehingga dapat dianggap bahwa penyesuaian linier optimal. Namun, jika titik -titik tersebut diamati bersama, tampaknya mereka memiliki kecenderungan untuk melengkung. Detail ini tidak direnungkan dalam model linier.

- Contoh 2

Untuk data yang sama dari contoh 1, buat grafik dispersi data. Pada kesempatan ini, tidak seperti contoh 1, diminta untuk melakukan penyesuaian regresi melalui fungsi potensial.

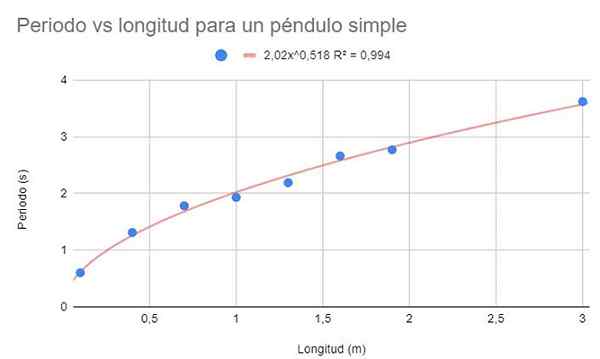Gambar 3. Solusi Grafis Latihan 2. Sumber: f. Zapata.

Tunjukkan juga fungsi penyesuaian dan koefisien penentuan -R -nya².

Larutan

Fungsi potensial adalah dari bentuk f (x) = kapak^B, di mana a dan b adalah konstan yang ditentukan dengan metode kuadrat minimum.

Gambar sebelumnya menunjukkan fungsi potensial dan parameternya, serta koefisien penentuan dengan nilai yang sangat tinggi 99%. Perhatikan bahwa data mengikuti kelengkungan garis tren.

Dapat melayani Anda: prinsip aditif

- Contoh 3

Dengan data yang sama dari Contoh 1 dan Contoh 2, buat penyesuaian polinomial -kedua. Tunjukkan grafik, polinomial penyesuaian dan koefisien penentuan r² koresponden.

Larutan

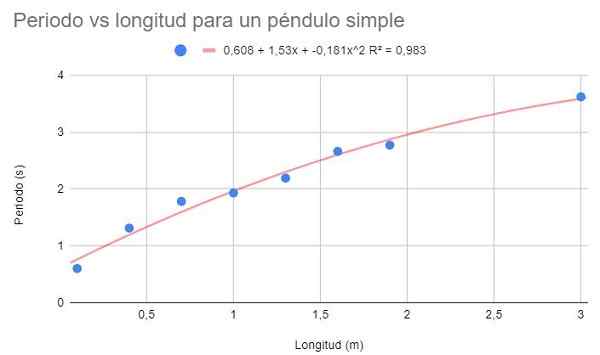Gambar 4. Latihan Grafis 3 Grafik. Sumber: f. Zapata.

Dengan penyesuaian polinomial tingkat kedua, garis tren dapat dilihat yang cocok dengan kelengkungan data. Demikian juga, koefisien penentuan berada di atas penyesuaian linier dan di bawah penyesuaian potensial.

Perbandingan penyesuaian

Dari tiga penyesuaian yang ditunjukkan, yang dengan koefisien penentuan yang lebih tinggi adalah penyesuaian potensial (Contoh 2).

Penyesuaian potensial bertepatan dengan teori fisik pendulum, yang, seperti diketahui, menetapkan bahwa periode pendulum sebanding dengan akar kuadrat dari panjangnya, menjadi konstan proporsionalitas 2π /√g di mana g adalah akselerasi gravitasi.

Jenis penyesuaian potensial ini tidak hanya memiliki koefisien penentuan tertinggi, tetapi konstanta eksponen dan proporsionalitas bertepatan dengan model fisik. 

Kesimpulan

-Penyesuaian regresi menentukan parameter fungsi yang bertujuan untuk menjelaskan data melalui metode kuadrat minimum. Metode ini terdiri dalam meminimalkan jumlah perbedaan kuadratik antara nilai dan penyesuaian dan nilai YI dari data untuk nilai XI dari data. Dengan cara ini parameter fungsi penyesuaian ditentukan.

-Seperti yang telah kita lihat, fungsi penyesuaian yang paling umum adalah lini, tetapi bukan satu -satunya, karena penyesuaian juga dapat berupa polinomik, potensial, eksponensial, logaritma dan lainnya. 

-Dalam kasus apa pun, koefisien penentuan tergantung pada data dan jenis penyesuaian dan merupakan indikasi dari kebaikan penyesuaian yang diterapkan.

-Akhirnya, koefisien penentuan menunjukkan persentase variabilitas total antara nilai dan data sehubungan dengan nilai ŷ dari penyesuaian untuk x yang diberikan.

Referensi

1. González c. Statistik umum. Pulih dari: tarwi.La Molina.Edu.pe
2. IACS. Institut Ilmu Kesehatan Aragon. Diperoleh dari: ICS-Aragon.com
3. Salazar c. dan Castillo s. Prinsip Statistik Dasar. (2018). Diperoleh dari: dspace.Uce.Edu.Ec
4. Superprof. Koefisien Penentuan. Pulih dari: superprof.adalah
5. USAC. Manual Statistik Deskriptif. (2011). Pulih dari: statistik.rekayasa.USAC.Edu.GT.
6. Wikipedia. Koefisien Penentuan. Pulih dari: is.Wikipedia.com.