Langkah -langkah posisi, kecenderungan sentral dan dispersi

Itu Ukuran kecenderungan pusat, dispersi dan posisi, Ini adalah nilai yang digunakan untuk menginterpretasikan dengan benar serangkaian data statistik. Ini dapat dikerjakan secara langsung, seperti yang diperoleh dari studi statistik, atau mereka dapat diatur dalam kelompok dengan frekuensi yang sama, memfasilitasi analisis.

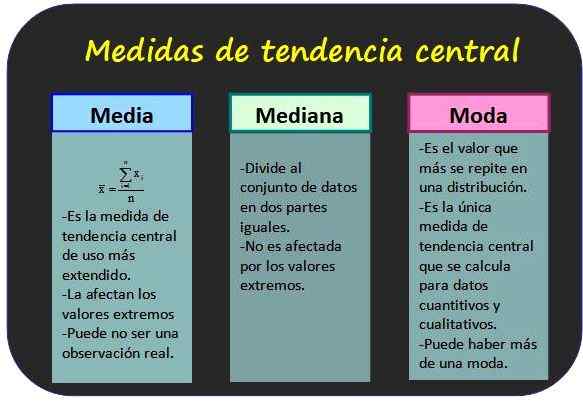
Tiga langkah tren pusat yang paling terkenal dan beberapa propertinya. Sumber: f. Zapata.

Ukuran kecenderungan sentral

Mereka memungkinkan untuk mengetahui tentang nilai apa data statistik dikelompokkan bersama.

Rata -rata aritmatika

Ini juga dikenal sebagai rata -rata nilai variabel dan diperoleh dengan menambahkan semua nilai dan membagi hasil dengan jumlah total data.

• Rata -rata aritmatika untuk data tanpa pengelompokan

Menjadi variabel X yang tidak ada data tanpa mengatur atau mengelompokkan, rata -rata aritmatika dihitung sebagai berikut:

Dan dalam notasi ringkasan:

Contoh

Pemilik asrama wisata gunung berniat mengetahui berapa hari rata -rata pengunjung tetap di fasilitas. Untuk melakukan ini, catatan hari -hari keabadian dari 20 kelompok wisatawan dilakukan, mendapatkan data berikut:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Rata -rata hari -hari masa tinggal wisatawan adalah:

= 2.5 hari

• Rata -rata aritmatika untuk data yang dikelompokkan

Jika data variabel diatur dalam tabel frekuensi absolut f_yo Dan pusat kelas adalah x₁, X₂,…, X_N, Rata -rata dihitung oleh:

Dalam penjumlahan musim panas:

Median

Median kelompok N nilai n variabel x adalah nilai sentral dari kelompok, asalkan nilai -nilai semakin dipesan. Dengan cara ini, setengah dari semua nilai lebih rendah dari mode dan setengah lainnya lebih besar.

• Media data yang tidak dikelompokkan

Kasus -kasus berikut dapat disajikan:

-Angka n nilai variabel x  aneh: Median adalah nilai yang hanya di tengah kelompok nilai:

-Angka n nilai variabel x pasangan: Dalam hal ini median dihitung sebagai rata -rata dari dua nilai sentral dari grup data:

Contoh

Untuk menemukan median data hostel wisata, mereka pertama kali dipesan dari yang paling kecil ke yang terbesar:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Itu dapat melayani Anda: apa frekuensi relatif dan bagaimana itu dihitung?

Nomor data bahkan, oleh karena itu ada dua data pusat: x₁₀ dan x_sebelas Dan karena keduanya bernilai 2, rata -rata juga.

Median = 2

• Media data yang dikelompokkan

Formula berikut digunakan:

Simbol dalam rumus berarti:

-C: Lebar interval yang mengandung median

-B_M: perbatasan bawah dari interval yang sama

-F_M: Jumlah pengamatan yang mengandung interval di mana median berada.

-N: Total Data.

-F_Bm: Jumlah pengamatan sebelum interval yang mengandung median.

Mode

Fashion untuk data yang tidak dikelompokkan adalah nilai frekuensi paling, sedangkan untuk data yang dikelompokkan ini adalah kelas paling frekuensi. Itu dianggap sebagai fashion sebagai data atau kelas distribusi yang paling representatif.

Dua karakteristik penting dari ukuran ini adalah bahwa set data dapat memiliki lebih dari satu mode, dan mode dapat ditentukan untuk data kuantitatif dan data kualitatif.

Contoh

Melanjutkan data asrama wisata, yang paling diulang adalah 1, oleh karena itu, hal yang paling umum adalah bahwa wisatawan tetap 1 hari di asrama.

Ukuran dispersi

Langkah -langkah dispersi menjelaskan bagaimana mengelompokkan data di sekitar langkah -langkah pusat.

Jangkauan

Itu dihitung dengan mengurangi data utama dan data minor. Jika perbedaan ini besar, itu adalah tanda bahwa data tersebar, sedangkan nilai -nilai kecil menunjukkan bahwa data dekat dengan rata -rata.

Contoh

Kisaran untuk data hostel wisata adalah:

Rentang = 5−1 = 4

Perbedaan

• Varians untuk data yang tidak dikelompokkan

Untuk menemukan varian s² Penting untuk terlebih dahulu mengetahui rata -rata aritmatika, maka perbedaan dihitung ke kuadrat antara setiap data dan rata -rata, semua ditambahkan dan dibagi dengan total pengamatan. Perbedaan ini dikenal sebagai penyimpangan.

Varians, yang selalu positif (atau nol), menunjukkan seberapa jauh pengamatan rata -rata: jika variannya tinggi, nilainya lebih tersebar daripada saat variannya kecil.

Contoh

Varian untuk data hostel wisata adalah:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Varian untuk data yang dikelompokkan

Untuk menemukan varian dari sekelompok data yang dikelompokkan, mereka diperlukan: i) rata -rata, ii) frekuensi f_yo  yang merupakan total data di setiap kelas dan iii) x_yo  atau nilai kelas:

Itu bisa melayani Anda: jenis segitiga

Deviasi standar

Deviasi standar adalah akar kuadrat positif dari varians, sehingga memiliki keunggulan dibandingkan varian: ia datang dalam unit yang sama dengan variabel yang diteliti dan dengan demikian memiliki ide yang lebih langsung daripada yang dekat atau jauh yang merupakan variabel rata -rata rata -rata.

• Deviasi standar untuk data yang tidak dikelompokkan

Ini ditentukan hanya dengan menemukan akar kuadrat dari varians untuk data yang belum dirpadah:

 Contoh

Deviasi standar untuk data hostel wisata adalah:

S = √ (s²) = √1.95 = 1.40

• Deviasi standar untuk data yang dikelompokkan

Ini dihitung dengan menemukan akar kuadrat dari varian untuk data yang dikelompokkan:

Langkah -langkah posisi

Langkah -langkah posisi membagi set data yang tertib menjadi bagian yang sama. Median, selain menjadi ukuran kecenderungan sentral juga merupakan ukuran posisi, karena membagi keseluruhan menjadi dua bagian yang sama. Tetapi Anda dapat memperoleh bagian yang lebih kecil dengan kuartil, desil dan persentil.

Kuartil

Kuartil membagi set menjadi empat bagian yang sama, masing -masing dengan 25 % dari data. Mereka dilambangkan sebagai q₁, Q₂ dan q₃ Dan mediannya adalah Q kuartil₂. Dengan cara ini, 25% dari data di bawah q kuartil₁, 50% di bawah q kuartil₂ atau median dan 75% di bawah kuartil Q₃.

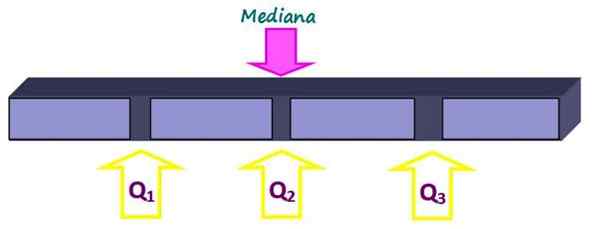Gambar 2. Kuartil membagi data yang ditetapkan menjadi empat bagian yang sama. Sumber: f. Zapata.

• Kuartil untuk data yang tidak dikelompokkan

Data dipesan dan totalnya dibagi menjadi 4 kelompok dengan jumlah data yang sama masing -masing. Posisi kuartil pertama ditemukan oleh:

Q₁ = (n+1)/4

Menjadi Total Data. Jika hasilnya adalah seluruh data yang sesuai dengan posisi itu, tetapi jika desimal, data yang sesuai dengan seluruh bagian dengan yang berikut ini dirata -rata, atau untuk presisi yang lebih besar, itu diinterpolasi secara linear antara data tersebut.

Contoh

Posisi q kuartil pertama₁ Untuk data asrama wisata adalah:

Q₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Ini adalah posisi kuartil 1 dan karena hasilnya desimal, data X data dicari₅ dan x_6, yang masing -masing x₅ = 1 dan x₆ = 1 dan mereka dirata -rata, dihasilkan:

Kuartil pertama = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Posisi q kuartil kedua₂ adalah:

Dapat melayani Anda: Jumlah teleskopik: bagaimana itu diselesaikan dan diselesaikan latihan

Q₂ = 2 (n+1)/4 = 10.5

Yang merupakan rata -rata antara x₁₀ dan x_sebelas dan bertepatan dengan median:

Kuartil kedua = median = 2

Posisi kuartil ketiga dihitung oleh:

Q₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Itu juga desimal, oleh karena itu x dirata -rata_limabelas dan x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Tapi karena keduanya bernilai 4:

Kuartil ketiga = 4

Rumus umum untuk posisi kuartil dalam data yang belum dirpadah adalah:

Q_k = K (n+1)/4

Dengan k = 1,2,3.

• Kuartil untuk data yang dikelompokkan

Mereka dihitung mirip dengan median:

Penjelasan simbol adalah:

-B_Q: Perbatasan interval yang lebih rendah yang mengandung kuartil

-C: Lebar interval itu

-F_Q: Jumlah pengamatan yang mengandung interval kuartil.

-N: Total Data.

-F_Bq: Jumlah data sebelum interval yang berisi kuartil.

Desil dan persentil

Desil dan persentil membagi data yang ditetapkan menjadi 10 bagian yang sama dan 100 bagian yang sama masing -masing, dan perhitungannya dilakukan dengan analog dengan kuartil.

• Desil dan persentil untuk data yang tidak dikelompokkan

Rumus masing -masing digunakan:

D_k = K (n+1)/10

Dengan k = 1,2,3… 9.

Desil d₅ Itu harus sama dengan median.

P_k = K (n+1)/100

Dengan k = 1,2,3 ... 99.

Persentil P_{lima puluh} Itu harus sama dengan median.

Contoh

Dalam contoh asrama wisata, posisi d₃ adalah:

D₃ = 3 (20+1)/10 = 6.3

Bagaimana angka desimal rata -rata x₆ dan x_7, keduanya sama dengan 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Berarti bahwa 3 persepuluh data di bawah x₇ = 1 dan yang tersisa di atas.

• Desil dan persentil untuk data yang dikelompokkan

Rumus analog dengan kuartil. D digunakan untuk menunjukkan desil dan p untuk persentil dan simbol ditafsirkan dengan cara yang sama:

Aturan empiris

Ketika data didistribusikan secara simetris dan distribusinya unimodal, ada aturan yang disebut  Aturan empiris salah satu Aturan 68 - 95 - 99, yang mengelompokkan mereka dalam interval berikut:

• 68% dari data dalam interval:

• 95% dari data dalam interval:

• 99% dari data dalam interval:

Contoh

Dalam interval apa 95% dari data hostel wisata?

Mereka sedang dalam interval: [2.5−1.40; 2.5+1.40] = [1.1; 3.9].

Referensi

1. Berenson, m. 1985. Statistik untuk Administrasi dan Ekonomi. Inter -American s.KE.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
4. Spiegel, m. 2009. Statistik. Seri Schaum. 4 ta. Edisi. Bukit McGraw.
5. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.