Koefisien Koefisien Poisson, Rumus, Nilai, Contoh

Dia Koefisien Poisson Itu adalah jumlah tanpa dimensi, karakteristik dari masing -masing bahan. Ini merupakan indikasi deformasi sepotong materi sebelum penerapan upaya tertentu.

Ketika bagian material yang mengalami ketegangan, atau kompresi, menderita deformasi, hasil bagi antara deformasi transversal dan deformasi longitudinal justru koefisien Poisson.

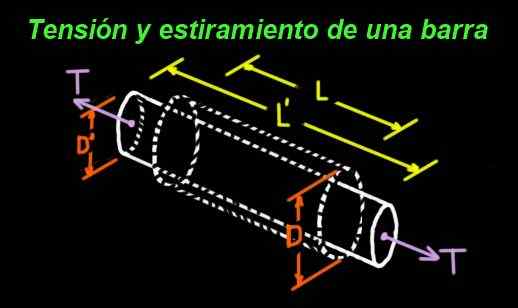
Gambar 1. Koefisien Poisson mengukur hubungan antara peregangan longitudinal dan penyempitan transversal. (Disiapkan oleh Ricardo Pérez)

Misalnya, silinder karet yang mengalami ketegangan di ujungnya direntangkan ke arah longitudinal, tetapi sangat sempit secara transversal. Gambar 1 menunjukkan bilah yang dimensinya yang aslinya adalah: Long L dan Diameter D.

Bilah mengalami tegangan T pada ujungnya, dan sebagai konsekuensi dari ketegangan ini mengalami peregangan, sehingga panjang baru adalah l '> l. Tetapi saat meregangkan, penyempitan diameternya juga terjadi pada nilai baru: D ' < D.

Hasil bagi antara peregangan (positif) dan penyempitan (negatif) dikalikan dengan (-1), adalah angka positif antara 0 dan 0,5. Nomor ini adalah koefisien Poisson ν yang disebut SO (surat Yunani).

[TOC]

Formula Koefisien Poisson

Untuk menghitung koefisien poisson, perlu menentukan deformasi unit longitudinal dan transversal.

Deformasi unit longitudinal ε_L Ini adalah peregangan yang dibagi antara panjang aslinya:

ε_L = (L ' - l) / l

Demikian pula, deformasi kesatuan melintang ε_T Ini adalah penyempitan radial yang dibagi antara diameter asli:

ε_T = (D ' - d) / d

Oleh karena itu, koefisien Poisson dihitung dengan rumus berikut:

ν = - ε_T / ε_L 

Hubungan dengan modul elastisitas dan modul kekakuan

Koefisien Poisson ν terkait dengan modul DAN elastisitas (atau modul muda) dan dengan modul kekakuan G, dengan formula berikut:

Dapat melayani Anda: Optik Geometris: Studi, Hukum, Aplikasi, Latihan Apa

ν = e /(2g) - 1

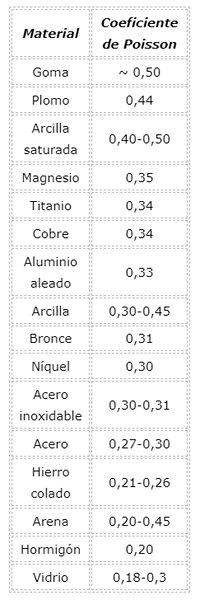
Nilai koefisien Poisson untuk material

Gambar 2. Baja tahan karat memiliki koefisien poisson antara 0,30 dan 0,31. Sumber: Pixabay.

Contoh perhitungan

Contoh 1

Batang dari bahan plastik tertentu memiliki panjang 150 mm dan bagian melingkar berdiameter 20 mm. Ketika gaya kompresi 612,25 kg-F mengalami gaya kompresi, pemendekan 14 mm diamati dan secara bersamaan peningkatan 0,85 mm dalam diameter batang.

Menghitung:

a) deformasi kesatuan longitudinal.

b) deformasi kesatuan transversal.

c) Koefisien Poisson dari materi itu.

d) Modul Elastisitas Muda yang sesuai dengan material.

e) modul kekakuan untuk plastik itu.

Solusi untuk

Ingatlah bahwa deformasi unit longitudinal εl adalah peregangan yang dibagi dengan panjang asli:

εl = (l ' - l) / l

εl = (-14 mm) / 150 mm = -0.0933

Perhatikan bahwa deformasi kesatuan longitudinal tidak dimensi, dan dalam hal ini telah memberikan negatif karena ada penurunan dimensi longitudinalnya.

Solusi b

Demikian pula, deformasi transversal kesatuan εt adalah penyempitan radial, dibagi dengan diameter asli:

εt = (d ' - d) / d

εt = (+0,85 mm) / 20 mm = 0,0425

Deformasi kesatuan transversal telah positif karena telah terjadi peningkatan diameter batang.

Solusi c

Untuk perhitungan koefisien Poisson, kita harus ingat bahwa itu didefinisikan sebagai negatif dari hasil bagi antara deformasi transversal dan deformasi longitudinal:

ν = - εt / εl 

ν = - 0.0425 / (-0.0933) = 0.4554

Harus diingat bahwa koefisien Poisson adalah angka tanpa dimensi positif dan untuk sebagian besar bahan adalah antara 0 dan 0,5.

Dapat melayani Anda: Darcy Law

Solusi d

Modul elastisitas Young, dilambangkan dengan huruf E, adalah proporsionalitas yang konstan dalam hukum Hooke. Melalui E, upaya normal σL terkait dengan deformasi kesatuan εl, sebagai berikut:

σl = e εl 

Upaya normal didefinisikan sebagai hasil bagi antara gaya normal (dalam hal ini sejajar dengan sumbu batang) dan bagian melintang:

σl = f / a = f / (π / 4 * d^2)

Dalam latihan ini, Force F adalah 612.25 kg-F, yang akan dibuat untuk Newton yang merupakan unit kekuatan:

F = 612.25 kg-f = 612.25 * 9.8 n = 6000 n = 6 kn

Untuk bagiannya, penampang A adalah:

A = (π/4 * d^2) = (3.1416/4) * (20 * 10^-3 m)^2 = 3.1416 * 10^-4 m^2

Akhirnya upaya normal yang diterapkan pada bilah adalah:

σl = f / a = 6000 n / 3,1416 * 10^-4 m^2 = 19.098.593 PA = 19.098 MPa

Untuk menghitung modul elastisitas anak yang kami jelaskan dan hukum Hooke σl = e εl:

E = σl / εl = 19.098.593 PA / 0,0933 = 204,7 MPa

Solusi e

Modul kekakuan R terkait dengan modul EG Young dan koefisien poisson ν dengan formula ini:

E / (2 g) = 1 + ν 

Dari sana Anda dapat menghapus g:

G = e / (2 (1 + ν)) = 204.7 MPa / (2 (1 + 0.4554)) = 70.33 MPa

Contoh 2

Anda memiliki kabel berdiameter 4 mm dan berdiameter 1 m. Mengetahui bahwa modul muda tembaga adalah 1.10000 MPa dan bahwa koefisien poisson-nya adalah 0,34, memperkirakan peregangan dan penyempitan dengan diameter yang menderita kawat ketika berat 100 kg-f-f.

Larutan

Pertama -tama perlu untuk menghitung upaya traksi normal yang diberikan berat pada kawat, mengikuti formula ini:

Dapat melayani Anda: vektor di ruang: cara grafik, aplikasi, latihan

σl = f / a = f / (π / 4 * d^2)

Gaya F adalah 980 N dan penampang adalah:

A = (π/4 * d^2) = (3,1416/4) * (4 * 10^-3 m)^2 = 1.2566 * 10^-5 m^2

Maka upaya traksi adalah:

σl = 980 n / 1.2566 * 10^-5 m^2 = 77.986.000 pa

Perhitungan deformasi kawat kesatuan

Modul elastisitas anak muda, yang dilambangkan dengan huruf E, adalah konstanta proporsionalitas dalam hukum Hooke yang menghubungkan upaya normal σl dengan deformasi kesatuan εl:

σl = e εl 

Dari sana deformasi kesatuan longitudinal dari kawat tembaga dapat dibersihkan:

εl = σl / e = 77.986 MPa / 110000 MPa = 7.09 * 10^-4

Perhitungan deformasi kesatuan transversal

Di sisi lain, untuk mengetahui deformasi kesatuan melintang, koefisien Poisson diterapkan:

ν = - εt / εl 

Akhirnya, Anda harus melintang deformasi kesatuan adalah: 

εt = -ν εl = -0.34 * 7.09 * 10 ^-4 = -2,41 * 10 ^-4

Perhitungan peregangan absolut kabel

Akhirnya, untuk mengetahui peregangan absolut dari kabel, hubungan berikut harus diterapkan:

Δl = εl * l = 7.09 * 10^-4 * 1 m = 7.09 * 10^-4 m = 0.709 mm

Yaitu, dengan berat itu kabel nyaris tidak membentang 0,709 milimeter.

Perhitungan penurunan diameter

Untuk mendapatkan diameter penyusutan absolut, kami menggunakan formula berikut:

Δd = εt * d = -2,41 * 10 ^-4 * 4 mm = -9,64 * 10 ^-4 mm = -0,000964 milimeter.

Diameter penyempitan ini sangat kecil sehingga sulit untuk dihargai dengan mata telanjang, bahkan pengukurannya membutuhkan instrumen presisi tinggi.

Referensi

1. Bir f ... mekanika material. Ke -5. Edisi. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Mekanika Bahan. Edisi Kedelapan. Prentice Hall. 2011. 3-60.
3. Gere J. Mekanika Bahan. Edisi Kedelapan. Pembelajaran Cengage. 4-220.
4. Giancoli, d. 2006. Fisika: Prinsip dengan aplikasi. Edisi ke -6. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Catatan Fisika Umum. Unam. 87-98.