Contoh koordinat bola dan latihan diselesaikan

Itu koordinat bola Mereka adalah sistem lokasi titik dalam ruang tiga dimensi yang terdiri dari koordinat radial dan dua koordinat sudut yang disebut koordinat kutub dan koordinat azimutal.

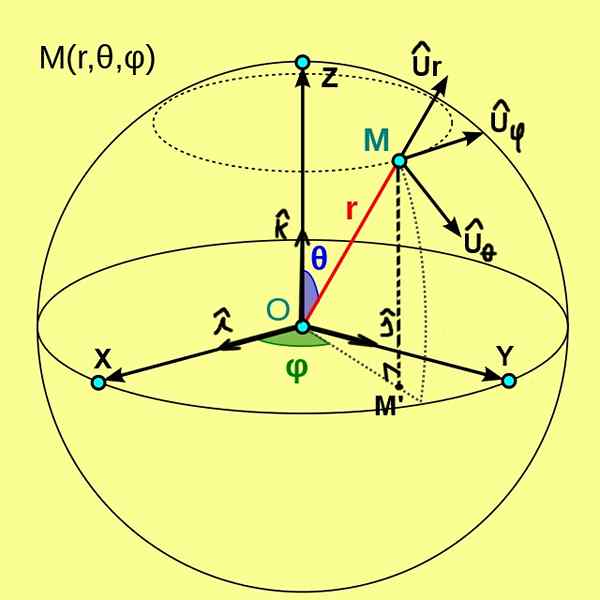
Pada Gambar 1, yang kita lihat di bawah ini, koordinat bola (r, θ, φ) dari suatu titik m ditampilkan. Koordinat ini dirujuk ke sistem ortogonal sumbu cartesian x, y, z asal atau.

Gambar 1. Koordinat bola (r, θ, φ) dari titik m. (Wikimedia Commons)

Dalam hal ini, koordinat R titik m adalah jarak dari titik ke titik asal atau. Koordinat kutub θ mewakili sudut antara semi -sumbu positif Z dan jari -jari vektor om. Sedangkan koordinat azimutal φ adalah sudut antara semi -axis X positif dan radius vektor om ', menjadi m' proyeksi ortogonal M pada bidang xy.

Koordinat radial R hanya mengambil nilai positif, tetapi jika suatu titik terletak di titik asal maka r = 0. Koordinat kutub θ mengambil sebagai nilai minimum 0º untuk titik yang terletak di semi -trib positif. Akhirnya, koordinat azimutal φ mengambil sebagai nilai minimum 0º dan level maksimum 360º.

0 ≤ r < ∞

0 ≤ θ ≤ 180º

0 ≤ φ  < 360º

[TOC]

Perubahan Koordinat

Selanjutnya, rumus yang memungkinkan koordinat cartesian (x, y, z) dari suatu titik m akan diberikan, dengan asumsi koordinat bola dari titik yang sama (r, θ, φ):

x = r sen (θ) cos (φ)

y = r sen (θ) sin (φ) 

z = r cos (θ)

Dengan cara yang sama, penting untuk menemukan hubungan untuk pindah dari koordinat cartesian (x, y, z) dari suatu titik yang diberikan kepada koordinat bola titik itu:

R = √ (x^2 + y^2 + z^2)

θ = arcan (√ (x^2 + y^2) / z)

Dapat melayani Anda: variabel acak diskrit

φ = arctan (y / x)

Basis vektor dalam koordinat bola

Dari koordinat bola, basis vektor dasar ortormal didefinisikan, yang dilambangkan oleh Ur, Uθ, Uφ. Gambar 1 menunjukkan tiga vektor unit ini, yang memiliki karakteristik berikut:

- Ur Ini adalah unit vektor tangen ke garis radial θ = ctte dan φ = ctte;

- Uθ Ini adalah vektor tangen unit ke busur φ = ctte dan r = ctte;

- Uφ Ini adalah vektor salib kesatuan ke arc r = ctte dan θ = ctte.

Elemen garis dan volume dalam koordinat bola

Posisi vektor titik di ruang dalam koordinat bola ditulis seperti ini:

R = r Ur

Tetapi variasi yang sangat kecil atau perpindahan titik dalam ruang tiga -dimensi, dalam koordinat ini diekspresikan oleh hubungan vektor berikut:

DR = dr Ur + r dθ Uθ + r sen (θ) dφ Uφ

Akhirnya, Volume Infinitesimal DV dalam koordinat bola ditulis seperti ini:

dv = r^2 sin (θ) dr dθ dφ

Hubungan ini sangat berguna untuk perhitungan integral garis dan volume dalam situasi fisik yang memiliki simetri bola.

Hubungan dengan koordinat geografis

Koordinat geografis dipahami bahwa mereka berfungsi untuk menemukan tempat di permukaan bumi. Sistem ini menggunakan koordinat garis lintang dan panjang untuk menemukan posisi di permukaan bumi.

Dalam sistem koordinat geografis, permukaan bumi seharusnya.

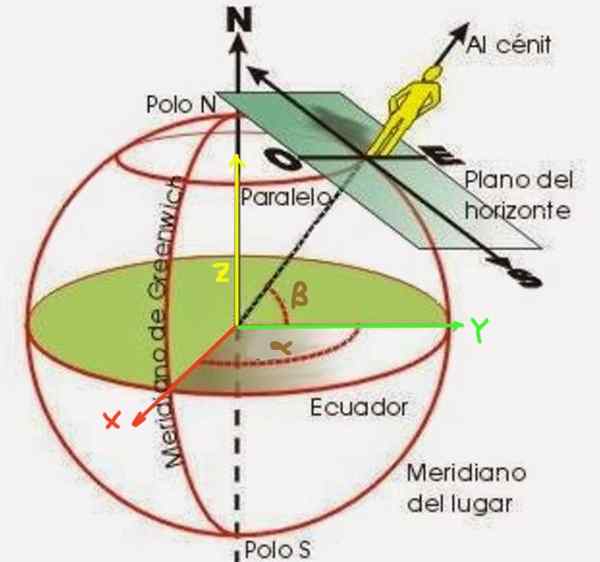Gambar 2. Panjang α dan β garis lintang pengamat di permukaan bumi.

Lintang β adalah sudut yang dibentuk oleh jari -jari yang dimulai dari pusat bumi ke titik yang ingin Anda posisikan. Diukur dari bidang khatulistiwa, seperti yang ditunjukkan pada Gambar 2. Di sisi lain, panjang α adalah sudut yang meridian titik yang menempatkan bentuk sehubungan dengan nol meridian (dikenal sebagai Greenwich Meridian).

Dapat melayani Anda: nilai relatif

Lintang bisa menjadi garis lintang utara atau selatan, tergantung pada apakah tempat yang berada di belahan bumi utara atau di belahan bumi selatan. Demikian pula, panjangnya bisa barat atau ini tergantung pada apakah lokasinya di barat atau timur nol meridian.

Rumus untuk berubah dari geografis ke bola

Untuk mendapatkan formula ini, hal pertama adalah membangun sistem koordinat. Pesawat XY dipilih bertepatan dengan bidang khatulistiwa, menjadi semi -axis X positif yang berjalan dari pusat bumi dan melalui nol meridian. Pada gilirannya, sumbu dan melewati 90º dan Meridian. Permukaan bumi memiliki radio RT.

Dengan sistem koordinat ini, transformasi geografis ke bola demikian:

αEβN → (RT, θ = 90º-β, φ = α)

αOβN → (RT, θ = 90º-β, φ = 360º-α)

αEβ → (RT, θ = 90º+β, φ = α)

αoβs → (RT, θ = 90º+β, φ = 360º-α) 

Contoh

Contoh 1

Koordinat geografis Palma de Mallorca (Spanyol) adalah:

Panjang Timur 38.847º dan Lintang Utara 39.570º. Untuk menentukan koordinat bola yang sesuai dengan Palma de Mallorca, rumus pertama dari rumus bagian sebelumnya diterapkan:

38.847ºE39.570ºN → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)

Maka koordinat bola adalah:

Palma de Mallorca: (r = 6371 km, θ = 50.43º, φ = 38.85º)

Dalam respons sebelumnya, r sama dengan jari -jari rata -rata bumi telah diambil.

Contoh 2

Mengetahui bahwa Kepulauan Falkland (Falkland) memiliki koordinat geografis 59ºO 51,75ºS, tentukan koordinat kutub yang sesuai. Ingatlah bahwa sumbu X beralih dari pusat bumi ke meridian 0º dan pada bidang khatulistiwa; Sumbu Y juga di bidang khatulistiwa dan melalui 90º West Meridian; Akhirnya sumbu z pada sumbu rotasi terestrial ke arah selatan-utara.

Dapat melayani Anda: Curtosis: Definisi, Jenis, Rumus, untuk apa, misalnya

Untuk kemudian menemukan koordinat bola yang sesuai, kami menggunakan rumus yang disajikan pada bagian sebelumnya:

59ºO 51.75ºS → (r = 6371 km, θ = 90º+51.75º, φ = 360º-59º) Artinya

Malvinas: (r = 6371 km, θ = 141.75º, φ = 301º)

Latihan

Latihan 1

Temukan koordinat Cartesian Palma de Mallorca di sistem referensi Cartesiano XYZ yang ditunjukkan pada Gambar 2.

Larutan: Sebelumnya, dalam Contoh 1 Koordinat bola diperoleh berdasarkan koordinat geografis Palma de Mallorca. Sehingga formula yang disajikan di atas dapat digunakan untuk beralih dari bola ke kartesia:

x = 6371 km sen (50.43º) cos (38.85º)

Y = 6371 km sen (50,43º) sen (38,85º) 

Z = 6371 km cos (50,43º)

Melakukan perhitungan yang sesuai adalah:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Latihan 2

Temukan koordinat Cartesian dari Kepulauan Falkland di sistem referensi Cartesiano XYZ yang ditunjukkan pada Gambar 2.

Larutan: Sebelumnya dalam Contoh 2 Koordinat bola diperoleh berdasarkan koordinat geografis Kepulauan Falkland. Sehingga formula yang disajikan di atas dapat digunakan untuk beralih dari bola ke kartesia:

x = 6371 km sen (141,75º) cos (301º)

y = 6371 km sen (141,75º) sen (301º) 

Z = 6371 km cos (141.75º)

Melakukan perhitungan yang sesuai diperoleh:

Kepulauan Falkland: (x = 2031 km, y = -3381 km, z = -5003)

Referensi

1. Arfken G dan Weber H. (2012). Metode Matematika untuk Fisikawan. Panduan komprehensif. Edisi ke -7. Pers Akademik. ISBN 978-0-12-384654-9
2. Perhitungan CC. Koordinat silinder dan bola terpecahkan. Pulih dari: perhitungan.Dc
3. Lokakarya Astronomi. Lintang dan bujur. Diperoleh dari: rate.Blogspot.com/
4. Weisstein, Eric W. “Koordinat Bulat.”Dari MathWorld-A Wolfram Web. Dipulihkan dari: MathWorld.Wolfram.com
5. Wikipedia. Sistem Koordinat Bola. Diperoleh dari: di.Wikipedia.com
6. Wikipedia. Bidang vektor dalam koordinat silinder dan bola. Diperoleh dari: di.Wikipedia.com